Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 11 Chân trời sáng tạo, hỗ trợ tối đa cho quá trình học tập của bạn.

Cho hai điểm B, C cố định trên đường tròn \(\left( {O;{\rm{ }}R} \right)\) và một điểm A thay đổi trên đường tròn đó

Đề bài

Cho hai điểm B, C cố định trên đường tròn \(\left( {O;{\rm{ }}R} \right)\) và một điểm A thay đổi trên đường tròn đó. Chứng minh trực tâm H của tam giác ABC luôn nằm trên một đường tròn cố định.

Phương pháp giải - Xem chi tiết Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo 1

Ta đi chứng minh trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn \(\left( {O;{\rm{ }}R} \right)\) qua phép tịnh tiến theo \(\overrightarrow {B'C} \)

Lời giải chi tiết

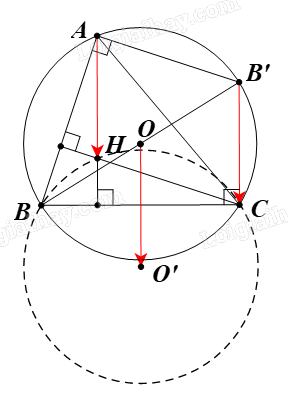
Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo 2

Kẻ đường kính BB’.

Do B, C cố định trên (O) nên B’, C cũng cố định trên (O).

Suy ra \(\overrightarrow {B'C} \) là vectơ không đổi.

Ta có \(\widehat {BCB'} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O)).

Suy ra \(BC \bot B'C.\)

Mà \(AH \bot BC\) (do H là trực tâm của ∆ABC).

Do đó \(AH//B'C\,\,\left( 1 \right)\)

Chứng minh tương tự, ta được \(AB'//CH{\rm{ }}\left( 2 \right)\)

Từ (1), (2), suy ra tứ giác AHCB’ là hình bình hành.

Suy ra \(AH{\rm{ }} = {\rm{ }}B'C.\)

Mà \(AH{\rm{ }}//{\rm{ }}B'C\) (chứng minh trên).

Vì vậy \(\overrightarrow {AH} = \overrightarrow {B'C} \)

Do đó \(H = {T_{\overrightarrow {B'C} }}\left( A \right)\).

Vậy khi A thay đổi trên đường tròn (O) thì trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn (O) là đường tròn (O’) qua \({{\rm{T}}_{\overrightarrow {B'C} }}\).

Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp

Bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định tính đơn điệu, cực trị và vẽ đồ thị hàm số. Việc nắm vững kiến thức nền tảng và rèn luyện kỹ năng giải bài tập là vô cùng quan trọng.

Nội dung chi tiết bài 4 trang 14

Bài 4 thường bao gồm các dạng bài tập sau:

Dạng 1: Xác định tập xác định của hàm số.
Dạng 2: Xét tính chẵn lẻ của hàm số.
Dạng 3: Tìm đạo hàm của hàm số và xác định các điểm cực trị.
Dạng 4: Vẽ đồ thị hàm số.
Dạng 5: Giải các bài toán liên quan đến ứng dụng của hàm số (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng).

Lời giải chi tiết bài 4 trang 14 (Ví dụ)

Đề bài: (Giả sử đề bài cụ thể của bài 4) Cho hàm số y = f(x) = x³ - 3x + 2. Tìm các điểm cực trị của hàm số.

Lời giải:

Bước 1: Tính đạo hàm f'(x) = 3x² - 3.
Bước 2: Giải phương trình f'(x) = 0 để tìm các điểm dừng: 3x² - 3 = 0 => x = ±1.
Bước 3: Xét dấu đạo hàm f'(x) trên các khoảng xác định để xác định tính đơn điệu của hàm số.
Bước 4: Kết luận: Hàm số đạt cực đại tại x = -1 với giá trị y = 4 và đạt cực tiểu tại x = 1 với giá trị y = 0.

Mẹo giải bài tập hiệu quả

Để giải bài tập Toán 11 Chân trời sáng tạo hiệu quả, bạn nên:

Nắm vững các định nghĩa, định lý và công thức liên quan đến hàm số và đồ thị.
Rèn luyện kỹ năng tính đạo hàm và giải phương trình.
Vẽ đồ thị hàm số để hiểu rõ hơn về tính chất của hàm số.
Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng bài tập và rèn luyện kỹ năng giải quyết vấn đề.

Tusach.vn – Đồng hành cùng bạn học Toán 11

Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 11 Chân trời sáng tạo. Chúng tôi cam kết hỗ trợ bạn học tập hiệu quả và đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!

Bảng tổng hợp các dạng bài tập thường gặp

Dạng bài tập	Phương pháp giải
Xác định tập xác định	Loại bỏ các giá trị làm mẫu số bằng 0 hoặc biểu thức dưới dấu căn âm.
Xét tính chẵn lẻ	Kiểm tra f(-x) = f(x) (hàm chẵn) hoặc f(-x) = -f(x) (hàm lẻ).
Tìm cực trị	Tính đạo hàm, giải phương trình đạo hàm bằng 0, xét dấu đạo hàm.

Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp

Nội dung chi tiết bài 4 trang 14

Lời giải chi tiết bài 4 trang 14 (Ví dụ)

Mẹo giải bài tập hiệu quả

Tusach.vn – Đồng hành cùng bạn học Toán 11

Bảng tổng hợp các dạng bài tập thường gặp

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN