Giải bài 6 trang 49 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 6 trang 49 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Bài 6 trang 49 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách Chuyên đề học tập Toán 11 Chân trời sáng tạo.
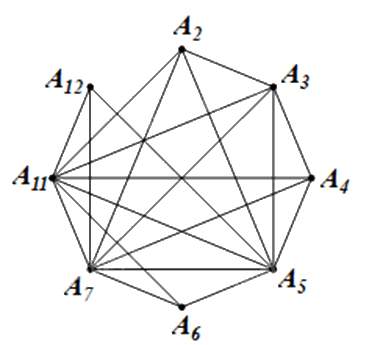
Cho tập hợp số V = {2; 3; 4; 5; 6; 7; 11; 12}.
Đề bài
Cho tập hợp số V = {2; 3; 4; 5; 6; 7; 11; 12}. Hãy vẽ đồ thị có các đỉnh biểu diễn các phần tử của V, hai đỉnh kề nhau nếu hai số mà chúng biểu diễn nguyên tố cùng nhau (tức có ước chung lớn nhất bằng 1).
Phương pháp giải - Xem chi tiết
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết
Trong tập hợp số V, ta có các cặp số sau nguyên tố cùng nhau:
• (2 và 3); (2 và 5); (2 và 7); (2 và 11);
• (3 và 4); (3 và 5); (3 và 7); (3 và 11);
• (4 và 5); (4 và 7); (4 và 11);
• (5 và 6); (5 và 7); (5 và 11); (5 và 12);
• (6 và 7); (6 và 11);
• (7 và 11); (7 và 12);
• (11 và 12).
Ta vẽ đồ thị G có 8 đỉnh A2, A3, A4, A5, A6, A7, A11, A12 lần lượt biểu diễn tám số 2; 3; 4; 5; 6; 7; 11; 12 trong tập hợp số V.
Hai đỉnh được nối bằng một cạnh nếu hai số mà chúng biểu diễn nguyên tố cùng nhau.
Ta có đồ thị G như sau:
Giải bài 6 trang 49 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài 6 trang 49 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung bài tập 6 trang 49
Bài 6 thường xoay quanh việc khảo sát hàm số bậc ba hoặc bậc bốn, yêu cầu học sinh:
- Tính đạo hàm cấp nhất và đạo hàm cấp hai của hàm số.
- Tìm các điểm cực trị của hàm số.
- Xác định khoảng đồng biến và nghịch biến của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết bài 6 trang 49
Để giải bài 6 trang 49 một cách hiệu quả, bạn cần thực hiện theo các bước sau:
- Bước 1: Xác định hàm số. Đọc kỹ đề bài để xác định chính xác hàm số cần khảo sát.
- Bước 2: Tính đạo hàm cấp nhất. Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm cấp nhất của hàm số.
- Bước 3: Tìm điểm cực trị. Giải phương trình đạo hàm cấp nhất bằng 0 để tìm các điểm cực trị. Sau đó, sử dụng đạo hàm cấp hai để xác định loại cực trị (cực đại hoặc cực tiểu).
- Bước 4: Xác định khoảng đơn điệu. Dựa vào dấu của đạo hàm cấp nhất, xác định khoảng đồng biến và nghịch biến của hàm số.
- Bước 5: Vẽ đồ thị hàm số. Sử dụng các thông tin đã tìm được (điểm cực trị, khoảng đơn điệu) để vẽ đồ thị hàm số.
Ví dụ minh họa (giả định một hàm số cụ thể)
Giả sử hàm số cần khảo sát là: f(x) = x3 - 3x2 + 2
Bước 1: f(x) = x3 - 3x2 + 2
Bước 2: f'(x) = 3x2 - 6x
Bước 3: Giải f'(x) = 0 => 3x2 - 6x = 0 => x = 0 hoặc x = 2. f''(x) = 6x - 6. f''(0) = -6 < 0 => x = 0 là điểm cực đại. f''(2) = 6 > 0 => x = 2 là điểm cực tiểu.
Bước 4: f'(x) > 0 khi x < 0 hoặc x > 2 => Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞). f'(x) < 0 khi 0 < x < 2 => Hàm số nghịch biến trên khoảng (0; 2).
Bước 5: Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số.
Mẹo giải bài tập đạo hàm hiệu quả
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
- Tham khảo các tài liệu tham khảo, sách giáo khoa, và các trang web học tập uy tín.
Tại sao nên chọn Tusach.vn để giải bài tập Toán 11?
Tusach.vn là một trang web học tập uy tín, cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 11. Chúng tôi có đội ngũ giáo viên giàu kinh nghiệm, luôn cập nhật nhanh chóng đáp án các bài tập mới nhất. Ngoài ra, Tusach.vn còn cung cấp nhiều tài liệu học tập hữu ích khác, giúp bạn học Toán 11 hiệu quả hơn.
Hãy truy cập Tusach.vn ngay hôm nay để giải bài 6 trang 49 Chuyên đề học tập Toán 11 Chân trời sáng tạo và khám phá thêm nhiều tài liệu học tập hữu ích khác!