Giải mục 1 trang 70, 71, 72 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 70, 71, 72 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 70, 71, 72 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
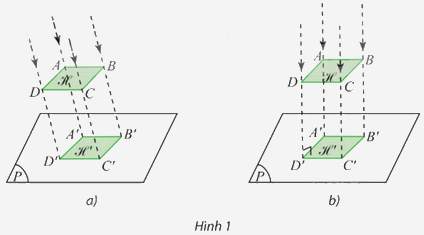
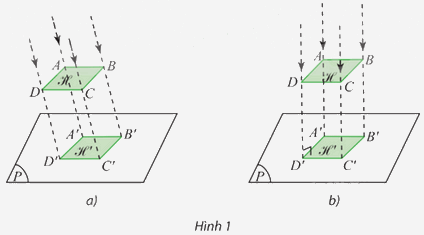
Hình 1 thể hiện hai cách chiếu hình ℋ thành hình ℋ ’ lên mặt phẳng (P).
Khám phá 1
Hình 1 thể hiện hai cách chiếu hình ℋ thành hình ℋ ’ lên mặt phẳng (P). Mô tả cách vẽ các đỉnh của hình chiếu ℋ ’ trong mỗi trường hợp.
Phương pháp giải:
Quan sát hình 1 để trả lời
Lời giải chi tiết:
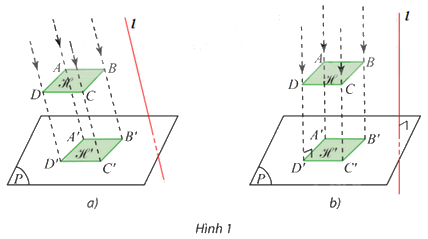
⦁ Hình 1a:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ cắt (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
⦁ Hình 1b:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ vuông góc với (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
Thực hành 1
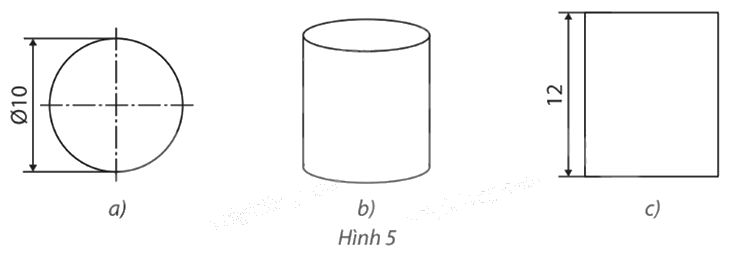
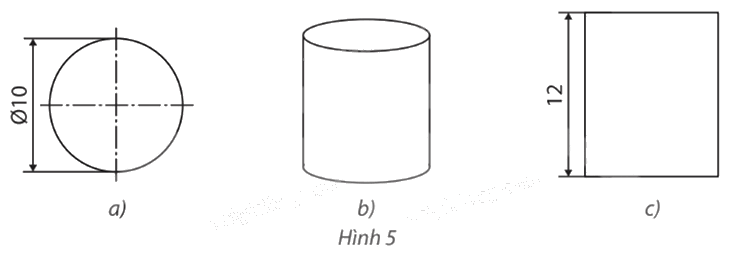
Dưới đây là ba hình biểu diễn của hình trụ có độ dài đường kính đáy bằng 10 cm và chiều cao bằng 12 cm. Chỉ ra phép chiếu được sử dụng tương ứng với mỗi hình.
Phương pháp giải:
Quan sát hình 5 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 5a là hình tròn có độ dài đường kính đáy bằng 10 cm nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với mặt đáy của hình trụ.
– Phép chiếu được sử dụng ở Hình 5b là phép chiếu song song.
– Hình 5c là hình chữ nhật có chiều dài bằng 12 cm (bằng chiều cao của hình trụ) nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với đường sinh của hình trụ.
Vận dụng 1
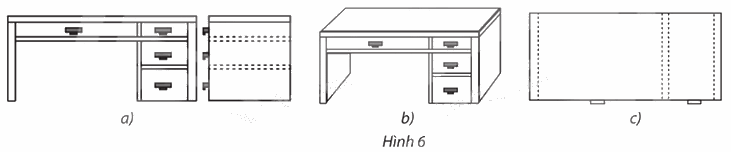
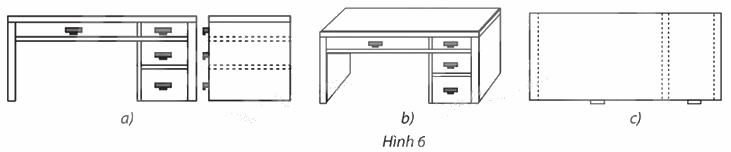
Phép chiếu nào được sử dụng để vẽ các hình biểu diễn của bàn làm việc trong Hình 6?
Phương pháp giải:
Quan sát hình 6 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 6a:
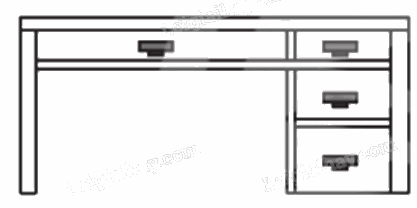
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt trước của bàn làm việc.
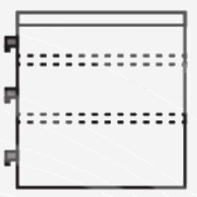
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bên của bàn làm việc.
– Hình 6b:
Phép chiếu được sử dụng ở Hình 6b là phép chiếu song song.
– Hình 6c:
Phép chiếu được sử dụng ở Hình 6c là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bàn của bàn làm việc.
- Khám phá 1
- Thực hành 1
- Vận dụng 1
Hình 1 thể hiện hai cách chiếu hình ℋ thành hình ℋ ’ lên mặt phẳng (P). Mô tả cách vẽ các đỉnh của hình chiếu ℋ ’ trong mỗi trường hợp.
Phương pháp giải:
Quan sát hình 1 để trả lời
Lời giải chi tiết:
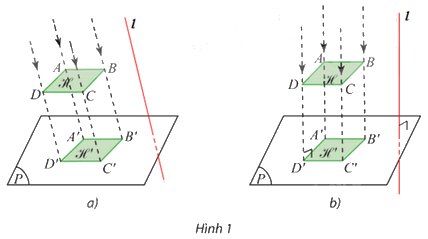
⦁ Hình 1a:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ cắt (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
⦁ Hình 1b:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ vuông góc với (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
Dưới đây là ba hình biểu diễn của hình trụ có độ dài đường kính đáy bằng 10 cm và chiều cao bằng 12 cm. Chỉ ra phép chiếu được sử dụng tương ứng với mỗi hình.
Phương pháp giải:
Quan sát hình 5 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 5a là hình tròn có độ dài đường kính đáy bằng 10 cm nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với mặt đáy của hình trụ.
– Phép chiếu được sử dụng ở Hình 5b là phép chiếu song song.
– Hình 5c là hình chữ nhật có chiều dài bằng 12 cm (bằng chiều cao của hình trụ) nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với đường sinh của hình trụ.
Phép chiếu nào được sử dụng để vẽ các hình biểu diễn của bàn làm việc trong Hình 6?
Phương pháp giải:
Quan sát hình 6 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 6a:
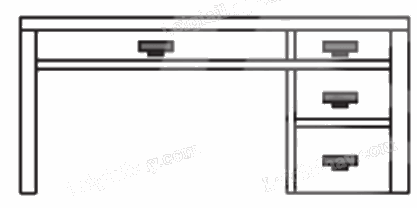
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt trước của bàn làm việc.
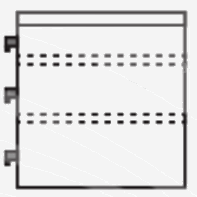
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bên của bàn làm việc.
– Hình 6b:
Phép chiếu được sử dụng ở Hình 6b là phép chiếu song song.
– Hình 6c:
Phép chiếu được sử dụng ở Hình 6c là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bàn của bàn làm việc.
Giải mục 1 trang 70, 71, 72 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề. Việc giải các bài tập trang 70, 71, 72 là bước quan trọng để củng cố lý thuyết và rèn luyện khả năng vận dụng kiến thức vào thực tế.
Nội dung chính của Mục 1 (trang 70, 71, 72)
Để hiểu rõ hơn về Mục 1, chúng ta cần xác định nội dung chính mà chuyên đề này đề cập đến. Thông thường, đây có thể là một chương mới về một khái niệm toán học, một định lý, hoặc một phương pháp giải toán cụ thể. Việc nắm bắt được nội dung chính sẽ giúp học sinh tập trung vào những kiến thức quan trọng nhất và giải quyết bài tập một cách hiệu quả.
Hướng dẫn giải chi tiết các bài tập trang 70, 71, 72
Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 1, trang 70, 71, 72 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo:
Bài 1: (Trang 70)
Đề bài: (Giả sử đề bài là một bài toán cụ thể về hàm số). Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và định lý liên quan).
Bài 2: (Trang 71)
Đề bài: (Giả sử đề bài là một bài toán về giới hạn). Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và định lý liên quan).
Bài 3: (Trang 72)
Đề bài: (Giả sử đề bài là một bài toán về đạo hàm). Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các công thức và định lý liên quan).
Các lưu ý khi giải bài tập
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của đề bài trước khi bắt đầu giải.
- Xác định kiến thức cần sử dụng: Xác định các công thức, định lý, và phương pháp giải toán liên quan đến đề bài.
- Trình bày lời giải rõ ràng, logic: Viết các bước giải một cách rõ ràng, dễ hiểu, và có tính logic.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Mở rộng kiến thức và luyện tập thêm
Để nắm vững kiến thức và kỹ năng giải toán, bạn nên:
- Đọc kỹ lại lý thuyết trong sách giáo khoa và tài liệu tham khảo.
- Giải thêm các bài tập tương tự trong sách bài tập và các nguồn tài liệu khác.
- Tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với bạn bè.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi hy vọng rằng những lời giải này sẽ giúp bạn học tập tốt hơn và đạt được kết quả cao trong môn Toán.
| Bài tập | Trang | Mức độ khó |
|---|---|---|
| Bài 1 | 70 | Dễ |
| Bài 2 | 71 | Trung bình |
| Bài 3 | 72 | Khó |
| Nguồn: Tusach.vn | ||