Giải mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 27, 28 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu nhất.
Bài giải này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi.
Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?
Khám phá 2
Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?
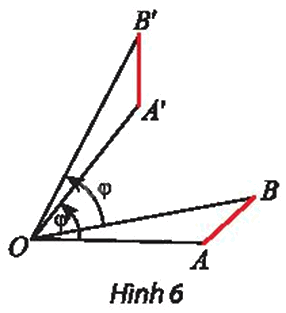
Phương pháp giải:
Quan sát hình 6 và xét các trường hợp bằng nhau của tam giác.
Lời giải chi tiết:
Ta có \({Q_{(O,{\rm{ }}\varphi )}}\) biến điểm A khác O thành điểm A’ sao cho \(OA{\rm{ }} = {\rm{ }}OA'\) và \(\left( {OA,{\rm{ }}OA'} \right){\rm{ }} = {\rm{ }}\varphi \;\) nên \(\widehat {AOA'} = \varphi \)
Tương tự, ta có \({Q_{\left( {O,{\rm{ }}\varphi } \right)}}\;\) biến điểm B khác O thành điểm B’ sao cho \(OB{\rm{ }} = {\rm{ }}OB'\) và \(\left( {OB,{\rm{ }}OB'} \right){\rm{ }} = {\rm{ }}\varphi \) nên \(\widehat {BO{B'}} = \varphi \)
Ta có \(\widehat {AOA'} = \widehat {BOB'}\left( { = \varphi } \right)\)
Suy ra \(\widehat {AOB} + \widehat {BOA'} = \widehat {BOA'} + \widehat {A'OB'}\)
Do đó \(\widehat {AOB} = \widehat {A'OB'}\)
Xét \(\Delta \) OAB và \(\Delta \) OA’B’, có:
OA = OA’ (chứng minh trên);
OB = OB’ (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (chứng minh trên).
Vậy \(\Delta \) OAB = \(\Delta \) OA’B’ (c.g.c).
Thực hành 2
Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay \({Q_{(I,{\rm{ }}90^\circ )}}\;\) của các hình sau:
a) Tam giác IAB;
b) Đường thẳng BC;
c) Đường tròn (B, a).
Phương pháp giải:
Để tìm ảnh của một hình, đường thẳng qua phép quay, ta tìm ảnh của các điểm thuộc hình, đường thẳng đó qua phép quay. Sau đó nối chúng với nhau.
Lời giải chi tiết:

a) Hình vuông ABCD có tâm I.
Suy ra AC ⊥ BD tại I và IA = IB = IC = ID.
Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm I thành điểm I.
⦁ Điểm A thành điểm D;
⦁ Điểm B thành điểm A;
Vậy ảnh của tam giác IAB qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là tam giác IDA.
b) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm B thành điểm A;
⦁ Điểm C thành điểm B.
Vậy ảnh của đường thẳng BC qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường thẳng AB.
c) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) biến điểm B thành điểm A.
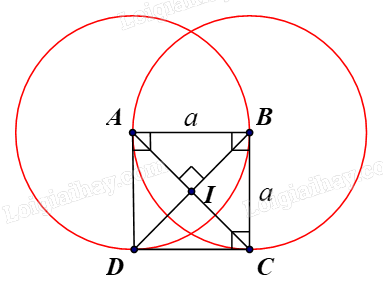
Vậy ảnh của đường tròn (B, a) qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường tròn (A, a).
Vận dụng 2
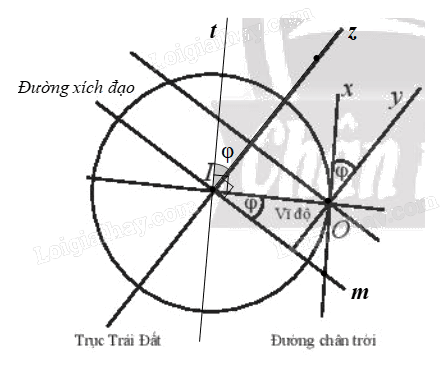
Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay \({Q_{(O,{\rm{ }}\varphi )}}\;\) biến tia Ox (song song với đường chân trời) thành tia Oy (song song với trục Trái Đất), nhờ đó đo được góc φ giữa trục của Trái Đất và đường chân trời tại vị trí của người đo. Hãy giải thích tại sao góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.

Phương pháp giải:
Quan sát hình 8 và suy luận để chứng minh
Lời giải chi tiết:
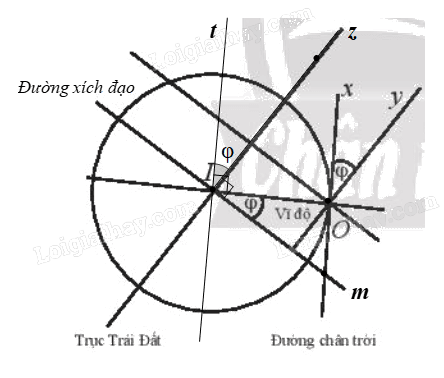
Gọi Iz là tia trùng với trục Trái Đất và nằm trên cùng một nửa mặt phẳng bờ IO chứa tia Ox, Oy.
Kẻ tia It song song với tia Ox.
Mà tia Oy song song với trục Trái Đất (giả thiết).
Do đó \(\widehat {tIz} = \widehat {xOy} = \varphi \)
Ta có tia Ox tiếp xúc với Trái Đất tại O.
Suy ra Ox là tiếp tuyến của đường tròn (I, IO).
Do đó \(Ox{\rm{ }} \bot {\rm{ }}IO.\)
Mà Ox // Ot nên \(Ot{\rm{ }} \bot {\rm{ }}IO.\)
Khi đó \(\widehat {tIz} + \widehat {zIO} = 90^\circ \,\,(1)\)
Gọi Im là tia trùng với đường xích đạo và nằm trên cùng một nửa mặt phẳng bờ Iz chứa đoạn thẳng IO.
Vì trục Trái Đất vuông góc với đường xích đạo nên ta có \(Iz \bot Im.\)
Suy ra \(\widehat {mIO} + \widehat {zIO} = 90^\circ \,\,(2)\)
Từ (1), (2), ta có \(\widehat {mIO} = \widehat {tIz} = \varphi \)
Vậy góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.
- Khám phá 2
- Thực hành 2
- Vận dụng 2
Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?
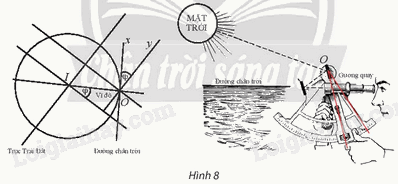
Phương pháp giải:
Quan sát hình 6 và xét các trường hợp bằng nhau của tam giác.
Lời giải chi tiết:
Ta có \({Q_{(O,{\rm{ }}\varphi )}}\) biến điểm A khác O thành điểm A’ sao cho \(OA{\rm{ }} = {\rm{ }}OA'\) và \(\left( {OA,{\rm{ }}OA'} \right){\rm{ }} = {\rm{ }}\varphi \;\) nên \(\widehat {AOA'} = \varphi \)
Tương tự, ta có \({Q_{\left( {O,{\rm{ }}\varphi } \right)}}\;\) biến điểm B khác O thành điểm B’ sao cho \(OB{\rm{ }} = {\rm{ }}OB'\) và \(\left( {OB,{\rm{ }}OB'} \right){\rm{ }} = {\rm{ }}\varphi \) nên \(\widehat {BO{B'}} = \varphi \)
Ta có \(\widehat {AOA'} = \widehat {BOB'}\left( { = \varphi } \right)\)
Suy ra \(\widehat {AOB} + \widehat {BOA'} = \widehat {BOA'} + \widehat {A'OB'}\)
Do đó \(\widehat {AOB} = \widehat {A'OB'}\)
Xét \(\Delta \) OAB và \(\Delta \) OA’B’, có:
OA = OA’ (chứng minh trên);
OB = OB’ (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (chứng minh trên).
Vậy \(\Delta \) OAB = \(\Delta \) OA’B’ (c.g.c).
Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay \({Q_{(I,{\rm{ }}90^\circ )}}\;\) của các hình sau:
a) Tam giác IAB;
b) Đường thẳng BC;
c) Đường tròn (B, a).
Phương pháp giải:
Để tìm ảnh của một hình, đường thẳng qua phép quay, ta tìm ảnh của các điểm thuộc hình, đường thẳng đó qua phép quay. Sau đó nối chúng với nhau.
Lời giải chi tiết:
a) Hình vuông ABCD có tâm I.
Suy ra AC ⊥ BD tại I và IA = IB = IC = ID.
Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm I thành điểm I.
⦁ Điểm A thành điểm D;
⦁ Điểm B thành điểm A;
Vậy ảnh của tam giác IAB qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là tam giác IDA.
b) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm B thành điểm A;
⦁ Điểm C thành điểm B.
Vậy ảnh của đường thẳng BC qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường thẳng AB.
c) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) biến điểm B thành điểm A.
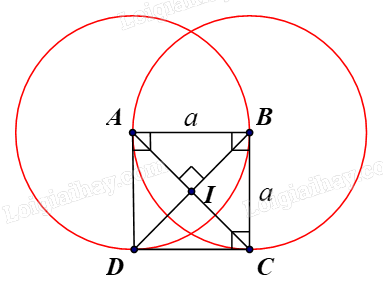
Vậy ảnh của đường tròn (B, a) qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường tròn (A, a).
Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay \({Q_{(O,{\rm{ }}\varphi )}}\;\) biến tia Ox (song song với đường chân trời) thành tia Oy (song song với trục Trái Đất), nhờ đó đo được góc φ giữa trục của Trái Đất và đường chân trời tại vị trí của người đo. Hãy giải thích tại sao góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.
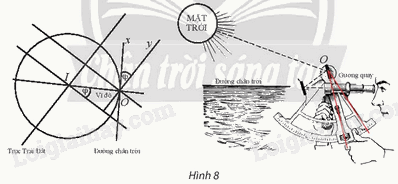
Phương pháp giải:
Quan sát hình 8 và suy luận để chứng minh
Lời giải chi tiết:
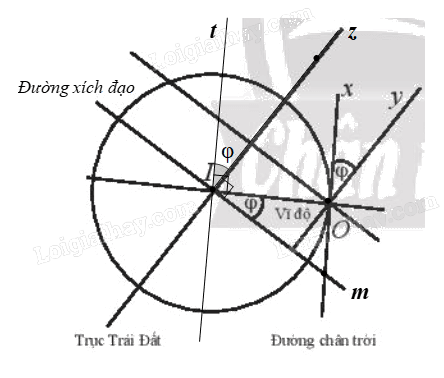
Gọi Iz là tia trùng với trục Trái Đất và nằm trên cùng một nửa mặt phẳng bờ IO chứa tia Ox, Oy.
Kẻ tia It song song với tia Ox.
Mà tia Oy song song với trục Trái Đất (giả thiết).
Do đó \(\widehat {tIz} = \widehat {xOy} = \varphi \)
Ta có tia Ox tiếp xúc với Trái Đất tại O.
Suy ra Ox là tiếp tuyến của đường tròn (I, IO).
Do đó \(Ox{\rm{ }} \bot {\rm{ }}IO.\)
Mà Ox // Ot nên \(Ot{\rm{ }} \bot {\rm{ }}IO.\)
Khi đó \(\widehat {tIz} + \widehat {zIO} = 90^\circ \,\,(1)\)
Gọi Im là tia trùng với đường xích đạo và nằm trên cùng một nửa mặt phẳng bờ Iz chứa đoạn thẳng IO.
Vì trục Trái Đất vuông góc với đường xích đạo nên ta có \(Iz \bot Im.\)
Suy ra \(\widehat {mIO} + \widehat {zIO} = 90^\circ \,\,(2)\)
Từ (1), (2), ta có \(\widehat {mIO} = \widehat {tIz} = \varphi \)
Vậy góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.
Giải mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 2 trang 27, 28 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào một số chủ đề quan trọng trong chương trình. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là rất cần thiết để các em học sinh có thể đạt kết quả tốt trong môn Toán.
Nội dung chính của Mục 2
Mục 2 thường bao gồm các nội dung sau:
- Các khái niệm cơ bản: Định nghĩa, tính chất, và các quy tắc liên quan đến chủ đề đang học.
- Ví dụ minh họa: Các bài toán mẫu được giải chi tiết để giúp học sinh hiểu rõ phương pháp giải.
- Bài tập luyện tập: Các bài tập với độ khó tăng dần để học sinh rèn luyện kỹ năng và củng cố kiến thức.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 27, 28:
Bài 1: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải:
- Bước 1: Phân tích đề bài và xác định yêu cầu.
- Bước 2: Áp dụng các kiến thức và công thức liên quan.
- Bước 3: Thực hiện các phép tính và đưa ra kết quả.
- Bước 4: Kiểm tra lại kết quả và đảm bảo tính chính xác.
Bài 2: (Bài tập luyện tập)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải thích chi tiết từng bước)
Mẹo giải toán hiệu quả
Để giải các bài tập trong Mục 2 trang 27, 28 một cách hiệu quả, các em học sinh nên:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Nắm vững các khái niệm và công thức cơ bản.
- Luyện tập thường xuyên để rèn luyện kỹ năng.
- Tham khảo các nguồn tài liệu tham khảo khác để mở rộng kiến thức.
- Hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn.
Ứng dụng của kiến thức trong Mục 2
Kiến thức và kỹ năng giải bài tập trong Mục 2 trang 27, 28 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, chẳng hạn như:
- Giải các bài toán thực tế.
- Nghiên cứu khoa học.
- Phát triển công nghệ.
Tusach.vn – Đồng hành cùng học sinh
Tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng, và lời giải bài tập để giúp các em học tập hiệu quả nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
Lưu ý: Các bài giải trên chỉ mang tính chất tham khảo. Các em học sinh nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng.
| Chủ đề | Nội dung chính |
|---|---|
| Đạo hàm | Khái niệm, quy tắc tính đạo hàm, ứng dụng của đạo hàm. |
| Tích phân | Khái niệm, phương pháp tính tích phân, ứng dụng của tích phân. |
| Nguồn: tusach.vn | |