Giải bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo.
Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau:
Đề bài
Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau:
– Lấy một tờ giấy hình vuông, gấp đôi, gấp tư rồi gấp làm tám (Hình 14a).
– Vẽ hoa và lá trên bề mặt tam giác (Hình 14b).
– Dùng kéo cắt theo đường đã vẽ (Hình 14c).
– Trải phẳng tờ giấy ra để thấy hoa văn trang trí gồm hoa và lá (Hình 14d).
Tìm tâm đối xứng và trục đối xứng của hoa văn vừa làm.

Phương pháp giải - Xem chi tiết
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục qua d biến H thành chính nó.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết
⦁ Giả sử ta chọn điểm O là giao điểm của các đường nếp gấp trên hình hoa văn vừa làm (như hình vẽ).

Lấy điểm A bất kì trên hình hoa văn vừa làm sao cho \(A{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm A’ trên hình hoa văn vừa làm sao cho \(A' = {\rm{ }}{Đ_O}\left( A \right).\)
Lấy điểm B trùng O. Khi đó ta có \(B{\rm{ }} = {\rm{ }}{Đ_O}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình hoa văn vừa làm, ta đều xác định được ảnh của các điểm đó qua ĐO trên hình hoa văn vừa làm.
Do đó phép đối xứng tâm O biến hình hoa văn vừa làm thành chính nó.
Vậy O là tâm đối xứng của hình hoa văn vừa làm.
⦁ Giả sử ta chọn đường thẳng d trên hình hoa văn vừa làm như hình vẽ.
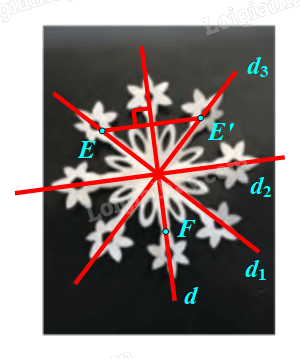
Lấy điểm E trên hình hoa văn vừa làm nhưng không nằm trên đường thẳng d.
Ta đặt \(E' = {\rm{ }}{Đ_d}\left( E \right).\)
Khi đó E’ nằm trên hình hoa văn vừa làm.
Lấy điểm F trên hình hoa văn vừa làm và nằm trên đường thẳng d.
Ta thấy \(F{\rm{ }} = {\rm{ }}{Đ_d}\left( F \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì trên hình hoa văn vừa làm, ta đều xác định được ảnh của điểm đó qua Đd trên hình hoa văn vừa làm.
Do đó phép đối xứng trục d biến hình hoa văn vừa làm thành chính nó.
Vậy d là trục đối xứng của hình hoa văn vừa làm.
Chú ý: Hình hoa văn vừa làm có 4 trục đối xứng \((d,{\rm{ }}{Đ_1},{\rm{ }}{Đ_2},{\rm{ }}{Đ_3}).\)
Giải bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung bài tập 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Bài tập 7 thường xoay quanh việc khảo sát hàm số bậc ba hoặc bậc bốn. Cụ thể, học sinh cần:
- Tính đạo hàm bậc nhất và đạo hàm bậc hai của hàm số.
- Tìm các điểm cực trị của hàm số.
- Xác định khoảng đồng biến và nghịch biến của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Để giải bài tập này một cách hiệu quả, các em cần thực hiện theo các bước sau:
- Bước 1: Xác định tập xác định của hàm số. Tập xác định là tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
- Bước 2: Tính đạo hàm bậc nhất. Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm y' của hàm số.
- Bước 3: Tìm các điểm cực trị. Giải phương trình y' = 0 để tìm các giá trị của x mà tại đó đạo hàm bằng 0. Các giá trị này là hoành độ của các điểm cực trị.
- Bước 4: Xác định loại điểm cực trị. Sử dụng dấu của đạo hàm bậc nhất để xác định xem mỗi điểm cực trị là điểm cực đại hay điểm cực tiểu.
- Bước 5: Tính đạo hàm bậc hai. Tìm đạo hàm y'' của hàm số.
- Bước 6: Tìm điểm uốn. Giải phương trình y'' = 0 để tìm các giá trị của x mà tại đó đạo hàm bậc hai bằng 0. Các giá trị này là hoành độ của các điểm uốn.
- Bước 7: Xác định khoảng lồi và lõm. Sử dụng dấu của đạo hàm bậc hai để xác định khoảng lồi và khoảng lõm của hàm số.
- Bước 8: Vẽ đồ thị hàm số. Dựa vào các thông tin đã tìm được, vẽ đồ thị hàm số.
Ví dụ minh họa
Giả sử hàm số cần khảo sát là y = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước trên để tìm ra các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số.
(Lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước tính toán cụ thể và kết quả).
Lưu ý khi giải bài tập
- Luôn kiểm tra lại các bước tính toán để tránh sai sót.
- Sử dụng máy tính cầm tay để hỗ trợ tính toán.
- Tham khảo các tài liệu tham khảo và bài giảng để hiểu rõ hơn về kiến thức.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn tự hào là một nguồn tài liệu học tập uy tín và chất lượng, cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và chuyên đề học tập Toán 11 Chân trời sáng tạo. Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu hữu ích khác!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 11 Chân trời sáng tạo | https://tusach.vn/toan-11-chan-troi-sang-tao |
| Chuyên đề học tập Toán 11 | https://tusach.vn/chuyen-de-toan-11 |