Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Chuyên đề 1. Phép biến hình phẳng
Bài 6. Phép vị tự

Giải bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 5 trang 36 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúng tôi sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.

Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.

Cho hai đường tròn (I; R) và (I’; R’) (Hình 12) có tâm phân biệt và bán kính khác nhau.

Đề bài

Cho hai đường tròn (I; R) và (I’; R’) (Hình 12) có tâm phân biệt và bán kính khác nhau. Hãy chứng minh có hai phép vị tự biến đường tròn (I; R) thành đường tròn (I’; R’).

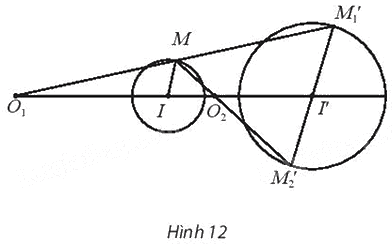
Giải bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiếtGiải bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo 2

Quan sát hình 12, suy luận để chứng minh.

Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.

Cần tìm được 2 giá trị của k thỏa mãn đề bài.

Lời giải chi tiết

Lấy điểm M bất kì thuộc \((I;{\rm{ }}R).\)

Đường thẳng qua I’ và song song với IM cắt đường tròn (I’; R’) tại hai điểm và (giả sử M, nằm cùng phía đối với đường thẳng II’ và M, nằm khác phía đối với đường thẳng II’).

Giả sử đường thẳng cắt đường thẳng II’ tại điểm O1 nằm ngoài đoạn OO’ và đường thẳng cắt đường thẳng II’ tại điểm O2 nằm trong đoạn II’.

Ta có biến đường tròn (I; R) thành đường tròn (I’; R’).

Suy ra \(R'{\rm{ }} = {\rm{ }}\left| k \right|.R.\)

Do đó \(|k| = \frac{{R'}}{R}\)

Mà \(k{\rm{ }} > {\rm{ }}0\) (do I, I’ nằm cùng phía đối với O1).

Suy ra \(k = \frac{{R'}}{R}\)

Ta có \({{\rm{V}}_{\left( {{{\rm{O}}_2},{\rm{k'}}} \right)}}\) biến đường tròn \(\left( {I;{\rm{ }}R} \right)\) thành đường tròn \(\left( {I';{\rm{ }}R'} \right).\)

Chứng minh tương tự, ta được khi I, I’ nằm khác phía đối với O2, ta có \(k' = - \frac{{R'}}{R}\)

Vậy ta có hai phép vị tự thỏa mãn yêu cầu bài toán là \({V_{\left( {{O_1},\frac{{R'}}{R}} \right)}}\) và \({V_{\left( {{O_2}, - \frac{{R'}}{R}} \right)}}\).

Giải bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan

Bài 5 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung chi tiết bài 5 trang 36

Bài 5 thường bao gồm các dạng bài tập sau:

  • Dạng 1: Tính đạo hàm của hàm số.
  • Dạng 2: Tìm cực trị của hàm số.
  • Dạng 3: Khảo sát sự biến thiên của hàm số.
  • Dạng 4: Ứng dụng đạo hàm để giải các bài toán tối ưu.

Lời giải chi tiết bài 5 trang 36

Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5 trang 36, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi:

Câu a: (Ví dụ minh họa)

Cho hàm số y = x3 - 3x2 + 2. Hãy tính đạo hàm y' của hàm số.

Lời giải:

Áp dụng quy tắc tính đạo hàm của tổng và tích, ta có:

y' = 3x2 - 6x

Câu b: (Ví dụ minh họa)

Tìm cực trị của hàm số y = x3 - 3x2 + 2.

Lời giải:

  1. Tính đạo hàm y' = 3x2 - 6x.
  2. Giải phương trình y' = 0 để tìm các điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
  3. Tính đạo hàm bậc hai y'' = 6x - 6.
  4. Kiểm tra dấu của y'' tại các điểm cực trị:
    • Tại x = 0, y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0. Giá trị cực đại là y(0) = 2.
    • Tại x = 2, y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là y(2) = -2.

Mẹo giải bài tập đạo hàm hiệu quả

Để giải các bài tập về đạo hàm một cách hiệu quả, các em học sinh cần:

  • Nắm vững các khái niệm cơ bản về đạo hàm.
  • Thuộc các quy tắc tính đạo hàm.
  • Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
  • Sử dụng máy tính bỏ túi để kiểm tra kết quả.

Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín

Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm:

  • Giải bài tập trong sách giáo khoa.
  • Giải bài tập trong Chuyên đề học tập.
  • Đề thi thử Toán 11.
  • Các bài viết hướng dẫn giải bài tập.

Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập!

Dạng bàiPhương pháp giải
Tính đạo hàmSử dụng quy tắc tính đạo hàm
Tìm cực trịGiải phương trình đạo hàm bằng 0

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN