Giải khởi động trang 14 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải khởi động trang 14 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Bài Giải khởi động trang 14 Chuyên đề học tập Toán 11 - Chân trời sáng tạo là phần mở đầu quan trọng để học sinh làm quen với các khái niệm và phương pháp mới trong chương trình học. Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo, đảm bảo hỗ trợ tối đa cho học sinh.
Trong các hình sau, hình nào có trục đối xứng?
Đề bài
Trong các hình sau, hình nào có trục đối xứng?
Có phép biến hình nào biến một nửa mỗi hình phẳng sau đây thành nửa còn lại không?

Phương pháp giải - Xem chi tiết
Quan sát hình vẽ, suy luận để trả lời
Lời giải chi tiết
+ Trong các hình đã cho, cả ba hình đều có trục đối xứng là đường thẳng màu vàng ở mỗi hình.
+ Ta xét hình chiếc lá:
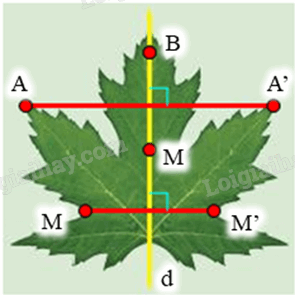
Lấy điểm A bất kì trên chiếc lá sao cho A không nằm trên trục đối xứng d của chiếc lá (hình vẽ).
Khi đó ta luôn xác định được một điểm A’ đối xứng với A qua d hay d là đường trung trực của đoạn thẳng AA’.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M không nằm trên d, ta đều xác định được một điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (1)
Lấy điểm B bất kì trên chiếc lá sao cho B nằm trên đường thẳng d (hình vẽ).
Khi đó ta có B đối xứng với chính nó qua d.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M nằm trên d thì ta luôn có M đối xứng với chính nó qua d (2)
Từ (1), (2), ta thu được phép biến hình biến một nửa chiếc lá thành nửa còn lại là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Chứng minh tương tự với hình cây thông và hình con bọ, ta cũng được kết quả như trên.
Vậy phép biến hình cần tìm là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d của mỗi hình phẳng thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Giải khởi động trang 14 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài Giải khởi động trang 14 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo đóng vai trò quan trọng trong việc kích thích tư duy và giúp học sinh ôn lại kiến thức nền tảng trước khi đi sâu vào các nội dung mới. Bài tập này thường mang tính chất gợi mở, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Nội dung bài Giải khởi động trang 14
Bài tập khởi động trang 14 thường tập trung vào việc:
- Ôn lại các khái niệm cơ bản về hàm số, đồ thị hàm số.
- Vận dụng các kiến thức về giới hạn để giải quyết các bài toán đơn giản.
- Rèn luyện kỹ năng tư duy logic và khả năng phân tích vấn đề.
Lời giải chi tiết và phương pháp giải
Tusach.vn cung cấp lời giải chi tiết cho từng bước của bài tập, giúp học sinh hiểu rõ cách tiếp cận và giải quyết vấn đề. Chúng tôi không chỉ đưa ra đáp án cuối cùng mà còn giải thích rõ ràng các bước thực hiện, các công thức và định lý được sử dụng. Điều này giúp học sinh tự tin hơn trong việc tự giải các bài tập tương tự.
Ví dụ minh họa
Giả sử bài tập yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1. Lời giải chi tiết sẽ như sau:
- Phân tích tử số: x^2 - 1 = (x - 1)(x + 1)
- Rút gọn hàm số: f(x) = (x - 1)(x + 1) / (x - 1) = x + 1 (với x ≠ 1)
- Tính giới hạn: lim (x→1) (x + 1) = 1 + 1 = 2
Như vậy, giới hạn của hàm số f(x) khi x tiến tới 1 là 2.
Tại sao nên chọn Tusach.vn để học Toán 11 Chân trời sáng tạo?
- Lời giải chính xác và đầy đủ: Chúng tôi luôn kiểm tra kỹ lưỡng các lời giải để đảm bảo tính chính xác và đầy đủ.
- Giải thích dễ hiểu: Các lời giải được trình bày một cách rõ ràng, dễ hiểu, phù hợp với trình độ của học sinh.
- Cập nhật nhanh chóng: Chúng tôi cập nhật nhanh chóng các lời giải bài tập mới nhất.
- Hỗ trợ nhiệt tình: Đội ngũ hỗ trợ của Tusach.vn luôn sẵn sàng giải đáp các thắc mắc của học sinh.
Các chuyên đề học tập Toán 11 khác
Ngoài bài Giải khởi động trang 14, Tusach.vn còn cung cấp lời giải chi tiết cho các bài tập khác trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo, bao gồm:
- Chuyên đề 1: Hàm số lượng giác
- Chuyên đề 2: Phương trình lượng giác
- Chuyên đề 3: Bất phương trình lượng giác
- ...
Lời khuyên khi học Toán 11
Để học tốt môn Toán 11, các em cần:
- Nắm vững kiến thức nền tảng.
- Luyện tập thường xuyên.
- Tìm kiếm sự giúp đỡ khi gặp khó khăn.
- Sử dụng các tài liệu học tập chất lượng.
Tusach.vn hy vọng sẽ là người bạn đồng hành đáng tin cậy của các em trên con đường chinh phục môn Toán 11!