Giải mục 1 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 30, 31, 32 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
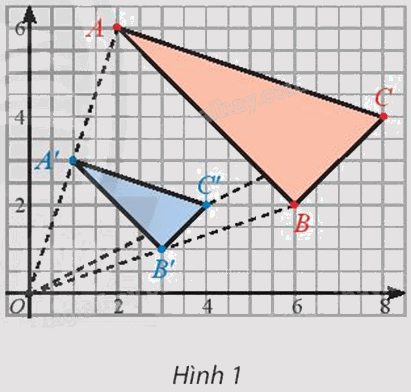
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
Thực hành 1
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; 9). Tìm tọa độ các điểm M1 và M2 lần lượt là ảnh của M qua các phép vị tự \({V_{\left( {O,{\rm{ }}3} \right)}}\;\) và \({V_{(O,{\rm{ }}-2)}}.\)
Phương pháp giải:
Nếu \({V_{(I,k)}}{\rm{[}}M(x,y){\rm{]}} = M'(x',y')\). Khi đó, \(\left\{ \begin{array}{l}x' - a = k(x - a)\\y' - b = k(y - b)\end{array} \right.\) với \(I(a;b)\)
Lời giải chi tiết:
Ta có \(\overrightarrow {OM} = \left( {3;9} \right)\)
⦁ Gọi \({M_1}({x_1};{\rm{ }}{y_1}),\;\) ta có \(\overrightarrow {O{M_1}} = \left( {{{\rm{x}}_1};{{\rm{y}}_1}} \right)\)
Theo đề, ta có \(\;{V_{(O,{\rm{ }}3)}}\left( M \right){\rm{ }} = {\rm{ }}{M_1}.\)
Suy ra \(\overrightarrow {O{M_1}} = 3\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_1} = 3.3 = 9}\\{{{\rm{y}}_1} = 3.9 = 27}\end{array}} \right.\)
Vì vậy tọa độ M1(9; 27).
⦁ Gọi \({M_2}({x_2};{\rm{ }}{y_2}),\;\) ta có \(\overrightarrow {O{M_2}} = \left( {{{\rm{x}}_2};{{\rm{y}}_2}} \right)\)
Theo đề, ta có \({V_{\left( {O,{\rm{ }}-2} \right)}}\left( M \right){\rm{ }} = {\rm{ }}{M_2}.\)
Suy ra \(\overrightarrow {O{M_2}} = - 2\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_2} = - 2.3 = - 6}\\{{{\rm{y}}_2} = - 2.9 = - 18}\end{array}} \right.\)
Vì vậy tọa độ \({M_2}\left( {-6;{\rm{ }}-18} \right).\)
Vậy \({M_1}\left( {9;{\rm{ }}27} \right),{M_2}\left( {-6;{\rm{ }}-18} \right).\)
Khám phá 1
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
a) Xét xem hai tam giác ABC và A’B’C’ đồng dạng không?
b) Thảo luận nhóm để tìm xem có phép biến hình nào biến tam giác ABC thành tam giác A’B’C’ không?
Phương pháp giải:
Quan sát hình 1 và chứng minh 2 tam giác đồng dạng theo trường hợp c.c.c
Lời giải chi tiết:
a) Ta có A’ là trung điểm của OA.
Suy ra \(OA' = \frac{1}{2}OA\) hay \(\frac{{OA'}}{{OA}} = \frac{1}{2}\)
Chứng minh tương tự, ta được \(\frac{{OB'}}{{OB}} = \frac{1}{2}\) và \(\frac{{OC'}}{{OC}} = \frac{1}{2}\)
Do \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\left( { = \frac{1}{2}} \right)\) nên áp dụng định lí Thales đảo, ta được A’B’ // AB.
Từ A’B’ // AB, theo hệ quả định lí Thales ta có: \(\frac{{A'B'}}{{AB}} = \frac{{OA'}}{{OA}} = \frac{1}{2}\) hay \(\frac{{AB}}{{A'B'}} = 2\)
Chứng minh tương tự, ta được \(\frac{{BC}}{{B'C'}} = 2\) và \(\frac{{AC}}{{A'C'}} = 2\)
Xét \(\Delta ABC{\rm{ }}\) và có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\left( { = 2} \right)\)
Vậy \(\Delta ABC\) đồng dạng với \(\Delta A\prime B\prime C\prime \) (c.c.c).
b) Để tìm phép biến hình biến ∆ABC thành ∆A’B’C’, ta tìm phép biến hình biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
Ta có A’ là trung điểm OA (giả thiết).
Suy ra \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \)
Do đó phép biến hình biến điểm A thành điểm A’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \,\,(1)\)
Thực hiện tương tự, ta được \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \)
Suy ra phép biến hình biến điểm B thành điểm B’ thỏa mãn \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \,\,(2)\)
Thực hiện tương tự, ta được \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \)
Do đó phép biến hình biến điểm C thành điểm C’ sao cho \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \,\,(3)\)
Từ (1), (2), (3), ta thu được phép biến hình biến \(\Delta ABC\) thành là phép biến hình biến ba điểm A, B, C thành ba điểm A’, B’, C’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} ,\,\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} ,\,\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \) với O là giao điểm của ba đường thẳng AA’, BB’, CC’.
Vận dụng 1
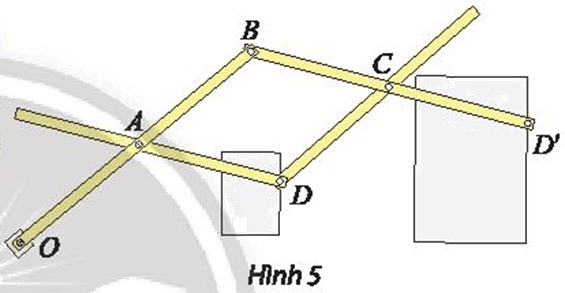
Thước vẽ truyền là một dụng cụ gồm bốn thanh gỗ hoặc kim loại được ghép với nhau nhờ bốn khớp xoay tại các điểm A, B, C, D sao cho ABCD là hình bình hành và ba điểm O, D, D’ thẳng hàng. Khi sử dụng, người vẽ ghim cố định điểm O xuống mặt giấy (thước vẫn có thể xoay quanh O). Đặt hai cây bút tại hai điểm D và D’. Khi đầu bút D vẽ hình ℋ, đầu bút D’ sẽ tự động vẽ truyền cho ta hình ℋ ’ là ảnh của ℋ.
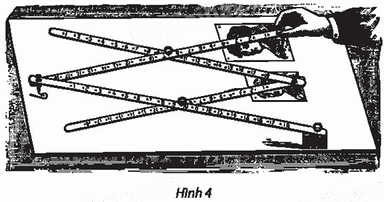
a) Xác định tâm và tỉ số k của phép vị tự được sử dụng trong cây thước vẽ truyền ở Hình 5.
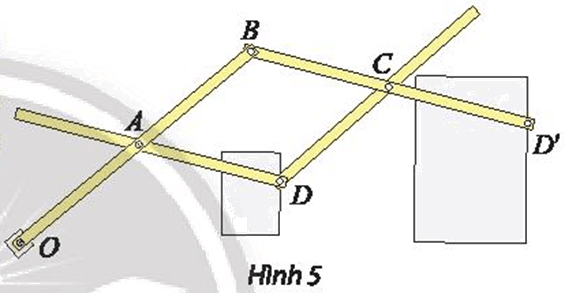
b) Nếu ngược lại cho đầu bút D’ vẽ hình ℋ ’ khi đó đầu bút D sẽ tự động vẽ truyền cho ta hình ℋ là ảnh của ℋ ’. Xác định phép vị tự trong trường hợp này.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
a) Do ba điểm O, D, D’ thẳng hàng (giả thiết), suy ra \(\overrightarrow {OD'} = k\overrightarrow {OD} \)
Do đó \({V_{(O,{\rm{ }}k)}}\left( D \right){\rm{ }} = {\rm{ }}D'\) và \(OD'{\rm{ }} = {\rm{ }}\left| k \right|.OD.\)
Vì D, D’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0.\)
Suy ra \(k = \frac{{OD'}}{{OD}}\)
Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).
Khi đó áp dụng định lí Thales, ta được \(k = \frac{{OD}}{{OD'}} = \frac{{OA}}{{OB}}\)
Vậy phép vị tự cần tìm là \({V_{\left( {O,\frac{{OA}}{{OB}}} \right)}}\)
b) Từ câu a, ta có \(\overrightarrow {OD'} = k\overrightarrow {OD} \,\,\left( {k{\rm{ }} > {\rm{ }}0} \right).\)
Suy ra \(\overrightarrow {OD} = \frac{1}{k}\overrightarrow {OD'} \)
Khi đó \({V_{\left( {O,\frac{1}{k}} \right)}}\left( {D'} \right) = D\)
Ta có \(\frac{1}{k} = 1:\frac{{OA}}{{OB}} = \frac{{OB}}{{OA}}\)
Vậy phép vị tự cần tìm là \({{\rm{V}}_{\left( {O,\frac{{OB}}{{OA}}} \right)}}\)
- Khám phá 1
- Thực hành 1
- Vận dụng 1
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
a) Xét xem hai tam giác ABC và A’B’C’ đồng dạng không?
b) Thảo luận nhóm để tìm xem có phép biến hình nào biến tam giác ABC thành tam giác A’B’C’ không?
Phương pháp giải:
Quan sát hình 1 và chứng minh 2 tam giác đồng dạng theo trường hợp c.c.c
Lời giải chi tiết:
a) Ta có A’ là trung điểm của OA.
Suy ra \(OA' = \frac{1}{2}OA\) hay \(\frac{{OA'}}{{OA}} = \frac{1}{2}\)
Chứng minh tương tự, ta được \(\frac{{OB'}}{{OB}} = \frac{1}{2}\) và \(\frac{{OC'}}{{OC}} = \frac{1}{2}\)
Do \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\left( { = \frac{1}{2}} \right)\) nên áp dụng định lí Thales đảo, ta được A’B’ // AB.
Từ A’B’ // AB, theo hệ quả định lí Thales ta có: \(\frac{{A'B'}}{{AB}} = \frac{{OA'}}{{OA}} = \frac{1}{2}\) hay \(\frac{{AB}}{{A'B'}} = 2\)
Chứng minh tương tự, ta được \(\frac{{BC}}{{B'C'}} = 2\) và \(\frac{{AC}}{{A'C'}} = 2\)
Xét \(\Delta ABC{\rm{ }}\) và có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\left( { = 2} \right)\)
Vậy \(\Delta ABC\) đồng dạng với \(\Delta A\prime B\prime C\prime \) (c.c.c).
b) Để tìm phép biến hình biến ∆ABC thành ∆A’B’C’, ta tìm phép biến hình biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
Ta có A’ là trung điểm OA (giả thiết).
Suy ra \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \)
Do đó phép biến hình biến điểm A thành điểm A’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \,\,(1)\)
Thực hiện tương tự, ta được \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \)
Suy ra phép biến hình biến điểm B thành điểm B’ thỏa mãn \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \,\,(2)\)
Thực hiện tương tự, ta được \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \)
Do đó phép biến hình biến điểm C thành điểm C’ sao cho \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \,\,(3)\)
Từ (1), (2), (3), ta thu được phép biến hình biến \(\Delta ABC\) thành là phép biến hình biến ba điểm A, B, C thành ba điểm A’, B’, C’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} ,\,\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} ,\,\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \) với O là giao điểm của ba đường thẳng AA’, BB’, CC’.
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; 9). Tìm tọa độ các điểm M1 và M2 lần lượt là ảnh của M qua các phép vị tự \({V_{\left( {O,{\rm{ }}3} \right)}}\;\) và \({V_{(O,{\rm{ }}-2)}}.\)
Phương pháp giải:
Nếu \({V_{(I,k)}}{\rm{[}}M(x,y){\rm{]}} = M'(x',y')\). Khi đó, \(\left\{ \begin{array}{l}x' - a = k(x - a)\\y' - b = k(y - b)\end{array} \right.\) với \(I(a;b)\)
Lời giải chi tiết:
Ta có \(\overrightarrow {OM} = \left( {3;9} \right)\)
⦁ Gọi \({M_1}({x_1};{\rm{ }}{y_1}),\;\) ta có \(\overrightarrow {O{M_1}} = \left( {{{\rm{x}}_1};{{\rm{y}}_1}} \right)\)
Theo đề, ta có \(\;{V_{(O,{\rm{ }}3)}}\left( M \right){\rm{ }} = {\rm{ }}{M_1}.\)
Suy ra \(\overrightarrow {O{M_1}} = 3\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_1} = 3.3 = 9}\\{{{\rm{y}}_1} = 3.9 = 27}\end{array}} \right.\)
Vì vậy tọa độ M1(9; 27).
⦁ Gọi \({M_2}({x_2};{\rm{ }}{y_2}),\;\) ta có \(\overrightarrow {O{M_2}} = \left( {{{\rm{x}}_2};{{\rm{y}}_2}} \right)\)
Theo đề, ta có \({V_{\left( {O,{\rm{ }}-2} \right)}}\left( M \right){\rm{ }} = {\rm{ }}{M_2}.\)
Suy ra \(\overrightarrow {O{M_2}} = - 2\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_2} = - 2.3 = - 6}\\{{{\rm{y}}_2} = - 2.9 = - 18}\end{array}} \right.\)
Vì vậy tọa độ \({M_2}\left( {-6;{\rm{ }}-18} \right).\)
Vậy \({M_1}\left( {9;{\rm{ }}27} \right),{M_2}\left( {-6;{\rm{ }}-18} \right).\)
Thước vẽ truyền là một dụng cụ gồm bốn thanh gỗ hoặc kim loại được ghép với nhau nhờ bốn khớp xoay tại các điểm A, B, C, D sao cho ABCD là hình bình hành và ba điểm O, D, D’ thẳng hàng. Khi sử dụng, người vẽ ghim cố định điểm O xuống mặt giấy (thước vẫn có thể xoay quanh O). Đặt hai cây bút tại hai điểm D và D’. Khi đầu bút D vẽ hình ℋ, đầu bút D’ sẽ tự động vẽ truyền cho ta hình ℋ ’ là ảnh của ℋ.
a) Xác định tâm và tỉ số k của phép vị tự được sử dụng trong cây thước vẽ truyền ở Hình 5.
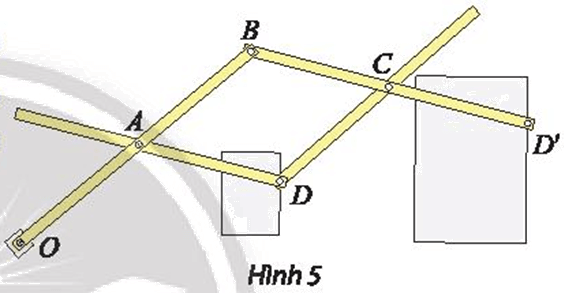
b) Nếu ngược lại cho đầu bút D’ vẽ hình ℋ ’ khi đó đầu bút D sẽ tự động vẽ truyền cho ta hình ℋ là ảnh của ℋ ’. Xác định phép vị tự trong trường hợp này.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
a) Do ba điểm O, D, D’ thẳng hàng (giả thiết), suy ra \(\overrightarrow {OD'} = k\overrightarrow {OD} \)
Do đó \({V_{(O,{\rm{ }}k)}}\left( D \right){\rm{ }} = {\rm{ }}D'\) và \(OD'{\rm{ }} = {\rm{ }}\left| k \right|.OD.\)
Vì D, D’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0.\)
Suy ra \(k = \frac{{OD'}}{{OD}}\)
Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).
Khi đó áp dụng định lí Thales, ta được \(k = \frac{{OD}}{{OD'}} = \frac{{OA}}{{OB}}\)
Vậy phép vị tự cần tìm là \({V_{\left( {O,\frac{{OA}}{{OB}}} \right)}}\)
b) Từ câu a, ta có \(\overrightarrow {OD'} = k\overrightarrow {OD} \,\,\left( {k{\rm{ }} > {\rm{ }}0} \right).\)
Suy ra \(\overrightarrow {OD} = \frac{1}{k}\overrightarrow {OD'} \)
Khi đó \({V_{\left( {O,\frac{1}{k}} \right)}}\left( {D'} \right) = D\)
Ta có \(\frac{1}{k} = 1:\frac{{OA}}{{OB}} = \frac{{OB}}{{OA}}\)
Vậy phép vị tự cần tìm là \({{\rm{V}}_{\left( {O,\frac{{OB}}{{OA}}} \right)}}\)
Giải mục 1 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Chuyên đề học tập Toán 11 - Chân trời sáng tạo là một tài liệu quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Mục 1 trang 30, 31, 32 tập trung vào một số nội dung cốt lõi, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong mục này, giúp các em học sinh tự tin hơn trong quá trình học tập.
Nội dung chính của Mục 1 trang 30, 31, 32
Mục 1 trang 30, 31, 32 thường bao gồm các bài tập liên quan đến:
- Đạo hàm của hàm số lượng giác: Tính đạo hàm của các hàm số sinx, cosx, tanx, cotx và các hàm hợp.
- Ứng dụng đạo hàm trong việc khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số lượng giác.
- Bài toán thực tế liên quan đến đạo hàm: Giải các bài toán về vận tốc, gia tốc, tối ưu hóa trong các tình huống thực tế.
Hướng dẫn giải chi tiết từng bài tập
Để giúp các em học sinh hiểu rõ hơn về cách giải các bài tập trong mục này, chúng ta sẽ đi vào giải chi tiết từng bài tập:
Bài 1: Tính đạo hàm của hàm số y = sin(2x + 1)
Lời giải:
Sử dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x + 1) * (2x + 1)' = 2cos(2x + 1)
Bài 2: Tìm cực trị của hàm số y = x + cosx
Lời giải:
Tính đạo hàm bậc nhất: y' = 1 - sinx
Giải phương trình y' = 0: 1 - sinx = 0 => sinx = 1 => x = π/2 + kπ (k ∈ Z)
Tính đạo hàm bậc hai: y'' = -cosx
Xét dấu y'' tại các điểm cực trị:
- Khi x = π/2 + kπ, y'' = -cos(π/2 + kπ) = 0
Do y'' = 0, ta cần xét dấu đạo hàm bậc ba để xác định cực trị. Tuy nhiên, trong trường hợp này, việc xét dấu đạo hàm bậc ba trở nên phức tạp. Thay vào đó, ta có thể xét dấu đạo hàm bậc nhất xung quanh các điểm cực trị để xác định tính chất của cực trị.
Bài 3: Giải bài toán thực tế về vận tốc
Đề bài: Một vật chuyển động theo phương trình s(t) = t2 + 2t (s tính bằng mét, t tính bằng giây). Tính vận tốc của vật tại thời điểm t = 3 giây.
Lời giải:
Vận tốc của vật là đạo hàm của quãng đường theo thời gian: v(t) = s'(t) = 2t + 2
Thay t = 3 vào công thức vận tốc, ta được: v(3) = 2 * 3 + 2 = 8 (m/s)
Mẹo học tập hiệu quả
Để học tốt môn Toán 11, đặc biệt là phần đạo hàm, các em học sinh nên:
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, công thức và quy tắc đạo hàm.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo các sách giáo khoa, sách bài tập, đề thi và các nguồn tài liệu trực tuyến.
- Hỏi thầy cô giáo: Nếu gặp khó khăn trong quá trình học tập, hãy mạnh dạn hỏi thầy cô giáo để được giải đáp.
Kết luận
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong Mục 1 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!