Giải mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, logic, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng.
Thực hành 2
Trong mặt phẳng tọa độ Oxy, tìm ảnh qua ĐO của
a) điểm M(3; –4);
b) đường thẳng d: x – 3y + 6 = 0;
c) đường tròn (C): (x + 2)2 + (y – 1)2 = 4.
Phương pháp giải:
Nếu \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
a) Gọi M’ là ảnh của M qua ĐO.
Suy ra O là trung điểm của MM’ với \(M\left( {3;{\rm{ }}-4} \right).\)
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_O} - {x_M} = 2.0 - 3 = - 3\\{y_{M'}} = 2{y_O} - {y_M} = 2.0 + 4 = 4\end{array} \right.\)
Vậy \(M'\left( {-3;{\rm{ }}4} \right).\)
b) • Chọn \(A\left( {0;{\rm{ }}2} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0.\)
Gọi A’là ảnh của A qua \({Đ_O}.\)
Suy ra O là trung điểm của AA’ với A(0; 2)
Do đó \(\left\{ \begin{array}{l}{x_{A'}} = 2{x_O} - {x_A} = 2.0 - 0 = 0\\{y_{A'}} = 2{y_O} - {y_A} = 2.0 - 2 = - 2\end{array} \right.\)
Vì vậy A’(0; –2).
• Đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\rm{\vec n}} = \left( {1; - 3} \right)\)
Gọi d’ là ảnh của d qua \({Đ_O}.\)
Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là \({\rm{\vec n}} = \left( {1; - 3} \right)\) làm vectơ pháp tuyến.
Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ \({\rm{\vec n}} = \left( {1; - 3} \right)\) pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x-3y-6 = 0.\)
c) Đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}\; = {\rm{ }}4\) có tâm I(–2; 1), bán kính R = 2.
Gọi (C’) là ảnh của (C) qua ĐO nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2.
Gọi I’= ĐO(I).
Suy ra O là trung điểm \(II'.\)
Do đó \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_O} - {x_I} = 2.0 + 2 = 2\\{y_{I'}} = 2{y_O} - {y_I} = 2.0 - 1 = - 1\end{array} \right.\)
Vì vậy tọa độ I’(2; –1).
Vậy đường tròn (C’) là ảnh của (C) qua ĐO, có tâm I’(2; –1) và R’ = 2 nên có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\)
Khám phá 2
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua ĐO. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.
Phương pháp giải:
Vẽ hình sau đó quan sát và so sánh
Lời giải chi tiết:

Theo đề, ta có \({Đ_O}\left( A \right){\rm{ }} = {\rm{ }}A'.\)
Suy ra O là trung điểm AA’, do đó \(OA{\rm{ }} = {\rm{ }}OA'.\)
Chứng minh tương tự, ta được \(OB{\rm{ }} = {\rm{ }}OB'.\)
Xét \(\Delta OAB\) và \(\Delta OA'B'\), có:
\(OA{\rm{ }} = {\rm{ }}OA'\) (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (đối đỉnh);
\(OB{\rm{ }} = {\rm{ }}OB'\) (chứng minh trên).
Do đó \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\left( {c.g.c} \right).\)
Suy ra \(A'B'{\rm{ }} = {\rm{ }}AB\) (cặp cạnh tương ứng).
Vậy \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\) và \(A'B'{\rm{ }} = {\rm{ }}AB.\)
Vận dụng 2
Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.
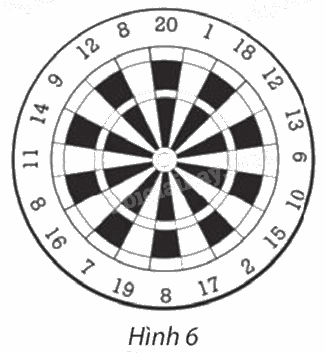
Phương pháp giải:
Quan sát hình 6 để tìm
Lời giải chi tiết:
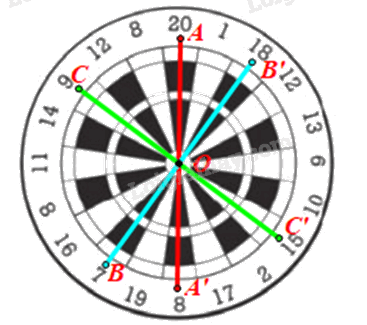
Gọi O là tâm bia.
• Lấy điểm A nằm trong ô có điểm ghi số 20. Lấy A’ đối xứng với A qua O.
Khi đó ta được điểm A’ nằm trong ô có điểm ghi số 8.
• Lấy điểm B nằm trong ô có điểm ghi số 7. Lấy B’ đối xứng với B qua O.
Khi đó ta được điểm B’ nằm trong ô có điểm ghi số 18.
• Lấy điểm C nằm trong ô có điểm ghi số 9. Lấy C’ đối xứng với C qua O.
Khi đó ta được điểm C’ nằm trong ô có điểm ghi số 15.
Vậy điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9 lần lượt là 8; 18; 15.
- Khám phá 2
- Thực hành 2
- Vận dụng 2
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua ĐO. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.
Phương pháp giải:
Vẽ hình sau đó quan sát và so sánh
Lời giải chi tiết:
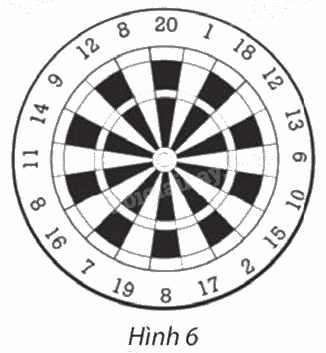
Theo đề, ta có \({Đ_O}\left( A \right){\rm{ }} = {\rm{ }}A'.\)
Suy ra O là trung điểm AA’, do đó \(OA{\rm{ }} = {\rm{ }}OA'.\)
Chứng minh tương tự, ta được \(OB{\rm{ }} = {\rm{ }}OB'.\)
Xét \(\Delta OAB\) và \(\Delta OA'B'\), có:
\(OA{\rm{ }} = {\rm{ }}OA'\) (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (đối đỉnh);
\(OB{\rm{ }} = {\rm{ }}OB'\) (chứng minh trên).
Do đó \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\left( {c.g.c} \right).\)
Suy ra \(A'B'{\rm{ }} = {\rm{ }}AB\) (cặp cạnh tương ứng).
Vậy \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\) và \(A'B'{\rm{ }} = {\rm{ }}AB.\)
Trong mặt phẳng tọa độ Oxy, tìm ảnh qua ĐO của
a) điểm M(3; –4);
b) đường thẳng d: x – 3y + 6 = 0;
c) đường tròn (C): (x + 2)2 + (y – 1)2 = 4.
Phương pháp giải:
Nếu \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
a) Gọi M’ là ảnh của M qua ĐO.
Suy ra O là trung điểm của MM’ với \(M\left( {3;{\rm{ }}-4} \right).\)
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_O} - {x_M} = 2.0 - 3 = - 3\\{y_{M'}} = 2{y_O} - {y_M} = 2.0 + 4 = 4\end{array} \right.\)
Vậy \(M'\left( {-3;{\rm{ }}4} \right).\)
b) • Chọn \(A\left( {0;{\rm{ }}2} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0.\)
Gọi A’là ảnh của A qua \({Đ_O}.\)
Suy ra O là trung điểm của AA’ với A(0; 2)
Do đó \(\left\{ \begin{array}{l}{x_{A'}} = 2{x_O} - {x_A} = 2.0 - 0 = 0\\{y_{A'}} = 2{y_O} - {y_A} = 2.0 - 2 = - 2\end{array} \right.\)
Vì vậy A’(0; –2).
• Đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\rm{\vec n}} = \left( {1; - 3} \right)\)
Gọi d’ là ảnh của d qua \({Đ_O}.\)
Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là \({\rm{\vec n}} = \left( {1; - 3} \right)\) làm vectơ pháp tuyến.
Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ \({\rm{\vec n}} = \left( {1; - 3} \right)\) pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x-3y-6 = 0.\)
c) Đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}\; = {\rm{ }}4\) có tâm I(–2; 1), bán kính R = 2.
Gọi (C’) là ảnh của (C) qua ĐO nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2.
Gọi I’= ĐO(I).
Suy ra O là trung điểm \(II'.\)
Do đó \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_O} - {x_I} = 2.0 + 2 = 2\\{y_{I'}} = 2{y_O} - {y_I} = 2.0 - 1 = - 1\end{array} \right.\)
Vì vậy tọa độ I’(2; –1).
Vậy đường tròn (C’) là ảnh của (C) qua ĐO, có tâm I’(2; –1) và R’ = 2 nên có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\)
Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.
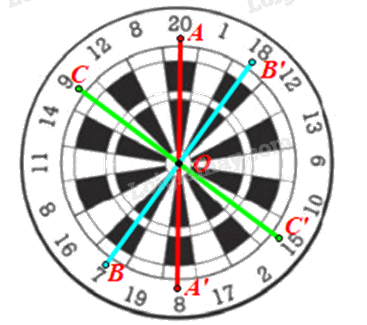
Phương pháp giải:
Quan sát hình 6 để tìm
Lời giải chi tiết:
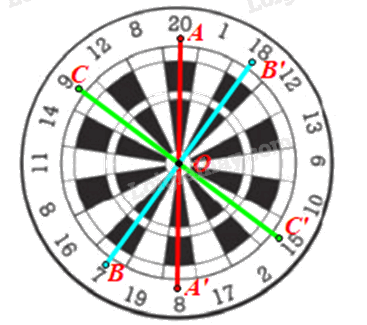
Gọi O là tâm bia.
• Lấy điểm A nằm trong ô có điểm ghi số 20. Lấy A’ đối xứng với A qua O.
Khi đó ta được điểm A’ nằm trong ô có điểm ghi số 8.
• Lấy điểm B nằm trong ô có điểm ghi số 7. Lấy B’ đối xứng với B qua O.
Khi đó ta được điểm B’ nằm trong ô có điểm ghi số 18.
• Lấy điểm C nằm trong ô có điểm ghi số 9. Lấy C’ đối xứng với C qua O.
Khi đó ta được điểm C’ nằm trong ô có điểm ghi số 15.
Vậy điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9 lần lượt là 8; 18; 15.
Giải mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 trang 21, 22 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức nền tảng và hiểu rõ yêu cầu của từng bài tập. Tusach.vn sẽ cung cấp một hướng dẫn chi tiết, từng bước để giúp bạn tự tin chinh phục các bài toán này.
Nội dung chính của Mục 2 trang 21, 22
Thông thường, mục này sẽ xoay quanh các chủ đề như:
- Đạo hàm của hàm số lượng giác: Tính đạo hàm của các hàm số sin, cos, tan, cot và các hàm hợp.
- Ứng dụng đạo hàm để khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số.
- Bài toán tối ưu: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 21, 22:
Bài 1: Tính đạo hàm của hàm số y = sin(2x)
Lời giải:
Sử dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x) * 2 = 2cos(2x)
Bài 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Lời giải:
- Tính đạo hàm bậc nhất: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 và x = 2
- Tính đạo hàm bậc hai: y'' = 6x - 6
- Xác định cực trị:
- Tại x = 0: y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0, ymax = 2
- Tại x = 2: y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, ymin = -2
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong Mục 2 trang 21, 22 một cách nhanh chóng và hiệu quả, bạn nên:
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
- Tham khảo các lời giải chi tiết trên Tusach.vn để hiểu rõ phương pháp giải.
Tầm quan trọng của việc giải bài tập
Việc giải bài tập là một bước quan trọng trong quá trình học tập Toán 11. Nó giúp bạn:
- Củng cố kiến thức đã học.
- Rèn luyện kỹ năng giải toán.
- Chuẩn bị cho các kỳ thi sắp tới.
Tusach.vn – Người bạn đồng hành đáng tin cậy
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chủ đề | Mức độ khó | Lời khuyên |
|---|---|---|
| Đạo hàm lượng giác | Trung bình | Nắm vững công thức |
| Khảo sát hàm số | Khó | Luyện tập nhiều |
| Bài toán tối ưu | Khó | Sử dụng đạo hàm |
| Chúc các bạn học tốt! | ||