Giải bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp học sinh hiểu bài và làm bài tập hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và dễ hiểu nhất, hỗ trợ tối đa cho quá trình học tập của bạn.
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25\) và đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25\) và đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
a) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục Ox.
b) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục Oy.
c) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0.\)
Phương pháp giải - Xem chi tiết
Nếu \(M' = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu\(M' = {Đ_{Oy}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết
Đường tròn (C) có tâm I(3; 4), bán kính R = 5.
a)
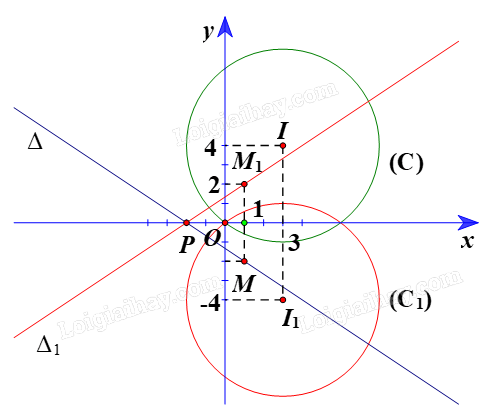
+ Gọi \(({C_1})\) là ảnh của (C) qua \({Đ_{Ox}}\), khi đó (C1) có tâm I1 là ảnh của I(3; 4) \({Đ_{Ox}}\) và bán kính \({R_1}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_1}\; = {\rm{ }}{Đ_{Ox}}\left( I \right).\)
Suy ra Ox là đường trung trực của đoạn \(\;I{I_1}\)
Do đó hai điểm I(3; 4) và I1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ \({I_1}\left( {3;{\rm{ }}-4} \right).\)
Vậy ảnh của đường tròn (C) qua ĐOx là đường tròn (C1) có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}4} \right)^2}\; = {\rm{ }}25.\)
+ Trục \(Ox:{\rm{ }}y{\rm{ }} = {\rm{ }}0.\)
Với y = 0, ta có \(2x{\rm{ }} + {\rm{ }}3.0{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} = {\rm{ }}-2.\)
Suy ra giao điểm của ∆ và trục Ox là điểm \(P\left( {-2;{\rm{ }}0} \right).\)
Khi đó \(P{\rm{ }} = {\rm{ }}{Đ_{Ox}}\left( P \right).\)
Chọn \(M\left( {1;{\rm{ }}-2} \right) \in \Delta \)
Gọi M1 và ∆1 theo thứ tự là ảnh của M và \(\Delta \) qua \({Đ_{Ox}}\)
Ta thấy Ox là đường trung trực của đoạn MM1.
Do đó hai điểm M(1; –2) và M1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ \({M_1}\left( {1;{\rm{ }}2} \right).\)
Ta có \(\overrightarrow {{M_1}P} = \left( { - 3; - 2} \right)\)
Đường thẳng \({\Delta _1}\;\) có vectơ chỉ phương \(\overrightarrow {{M_1}P} = \left( { - 3; - 2} \right)\)
Suy ra \({\Delta _1}\;\) có vectơ pháp tuyến \({\vec n_{{\Delta _1}}} = \left( {2; - 3} \right)\)
Vậy đường thẳng \({\Delta _1}\;\) đi qua P(–2; 0) và có vectơ pháp tuyến \({\vec n_{{\Delta _1}}} = \left( {2; - 3} \right)\) nên có phương trình là:
\(2\left( {x{\rm{ }} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }}-{\rm{ }}0} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 2x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
b)
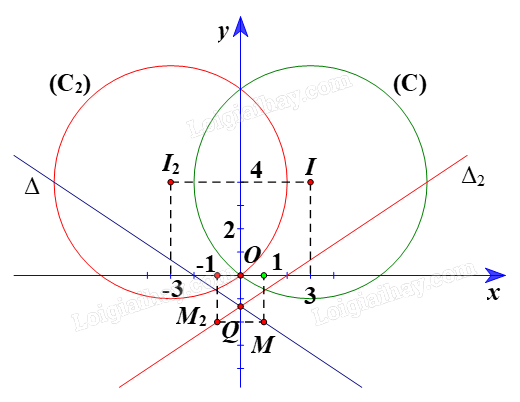
+ Gọi \(({C_2})\) là ảnh của (C) qua \({Đ_{Oy}}\), khi đó \(({C_2})\) có tâm \({I_{2\;}}\) là ảnh của \(I\left( {3;{\rm{ }}4} \right)\)qua \({Đ_{Oy}}\) và bán kính \({R_2}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_2}\; = {\rm{ }}{Đ_{Oy}}\left( I \right).\)
Suy ra Oy là đường trung trực của đoạn \(I{I_2}.\)
Do đó hai điểm I(3; 4) và \({I_{2\;}}\) có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ \({I_2}\left( {-3;{\rm{ }}4} \right).\)
Vậy ảnh của đường tròn (C) qua \({Đ_{Oy}}\) là đường tròn \(({C_2})\) có phương trình là:
\({\left( {x{\rm{ }} + {\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25.\)
+ Trục \(Oy:{\rm{ }}x{\rm{ }} = {\rm{ }}0.\)
Với x = 0, ta có \(2.0{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0{\rm{ }} \Leftrightarrow y = - \frac{4}{3}\)
Suy ra giao điểm của \(\Delta \) và trục Oy là điểm \(Q\left( {0; - \frac{4}{3}} \right)\)
Khi đó \(Q{\rm{ }} = {\rm{ }}{Đ_{Oy}}\left( Q \right).\)
Chọn \(M\left( {1;{\rm{ }}-2} \right) \in \Delta \)
Gọi \({M_2}\;\) và \({\Delta _2}\;\) theo thứ tự là ảnh của M và \(\Delta \) qua \({Đ_{Oy}}\)
Ta thấy Oy là đường trung trực của đoạn \(M{M_2}.\)
Do đó hai điểm M(1; –2) và M2 có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ \({M_2}\left( {-1;{\rm{ }}-2} \right).\)
Ta có \(\overrightarrow {{M_2}Q} = \left( {1;\frac{2}{3}} \right)\)
Đường thẳng ∆2 có vectơ chỉ phương \({\vec u_2} = 3\overrightarrow {{M_2}Q} = \left( {3;2} \right)\)
Suy ra ∆2 có vectơ pháp tuyến \({\vec n_{{\Delta _2}}} = \left( {2; - 3} \right)\)
Vậy đường thẳng \({\Delta _2}\) đi qua \({M_2}\left( {-1;{\rm{ }}-2} \right)\) và có vectơ pháp tuyến \({\vec n_{{\Delta _2}}} = \left( {2; - 3} \right)\) nên có phương trình là:
\(2\left( {x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 2x{\rm{ }}-{\rm{ }}3y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
c)
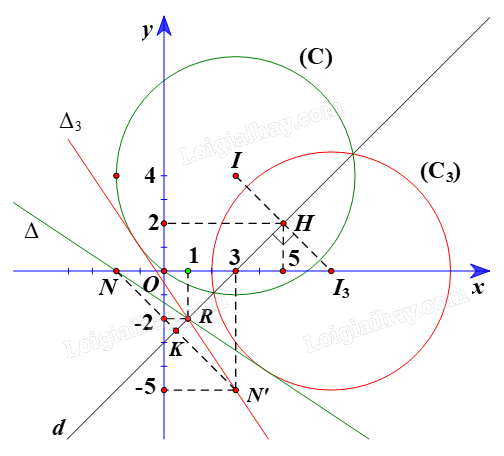
+ Gọi \({\rm{ }}({C_3})\) là ảnh của (C) qua \({Đ_d}\), khi đó \(({C_2})\) có tâm \({I_3}\) là ảnh của I(3; 4) qua Đd và bán kính \({R_3}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_3}\; = {\rm{ }}{Đ_d}\left( I \right).\)
Suy ra d là đường trung trực của đoạn II3 nên II3 ⊥ d tại trung điểm của II3.
Mà đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 1} \right)\)
Suy ra đường thẳng II3 có vectơ chỉ phương \({\vec n_d} = \left( {1; - 1} \right)\)
Do đó đường thẳng II3 có vectơ pháp tuyến \(\vec u = \left( {1;1} \right)\)
Vì vậy đường thẳng II3 đi qua điểm I(3; 4) và nhận \(\vec u = \left( {1;1} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}3} \right){\rm{ }} + {\rm{ }}1\left( {y{\rm{ }}-{\rm{ }}4} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\)
Gọi H là giao điểm của \(I{I_3}\) và đường thẳng d.
Suy ra tọa độ H thỏa mãn hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{{\rm{x}} - {\rm{y}} - 3 = 0}\\{{\rm{x}} + {\rm{y}} - 7 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = 5}\\{{\rm{y}} = 2}\end{array}} \right.\)
Do đó tọa độ \(H\left( {5;{\rm{ }}2} \right).\)
Ta có H là trung điểm \(I{I_3}.\)
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_{{{\rm{I}}_3}}} = 2{{\rm{x}}_{\rm{H}}} - {{\rm{x}}_{\rm{I}}} = 2.5 - 3 = 7}\\{{{\rm{y}}_{{{\rm{I}}_3}}} = 2{{\rm{y}}_{\rm{H}}} - {{\rm{y}}_{\rm{I}}} = 2.2 - 4 = 0}\end{array}} \right.\)
Do đó tọa độ \({I_3}\left( {7;{\rm{ }}0} \right).\)
Vậy ảnh của đường tròn (C) qua \({Đ_d}\) là đường tròn \(({C_3})\) có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}7} \right)^2}\; + {\rm{ }}{y^2}\; = {\rm{ }}25.\)
+ Gọi R là giao điểm của \(\Delta \) và d.
Suy ra tọa độ R thỏa mãn hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 3{\rm{y}} + 4 = 0}\\{{\rm{x}} - {\rm{y}} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = 1}\\{{\rm{y}} = - 2}\end{array}} \right.\)
Do đó tọa độ R(1; –2).
Khi đó \(R{\rm{ }} = {\rm{ }}{Đ_d}\left( R \right).\)
Chọn \(N\left( {-2;{\rm{ }}0} \right) \in \Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
Gọi N’ và \({\Delta _3}\) theo thứ tự là ảnh của N và \(\Delta \) qua \({Đ_d}\).
Ta thấy d là đường trung trực của đoạn NN’.
Mà đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 1} \right)\)
Suy ra đường thẳng NN’ có vectơ chỉ phương \({\vec n_d} = \left( {1; - 1} \right)\)
Do đó đường thẳng NN’ có vectơ pháp tuyến \(\vec u = \left( {1;1} \right)\)
Vì vậy đường thẳng NN’ đi qua N(–2; 0) và nhận \(\vec u = \left( {1;1} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} + {\rm{ }}1\left( {y{\rm{ }}-{\rm{ }}0} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0.\)
Gọi K là giao điểm của NN’ và đường thẳng d.
Suy ra tọa độ K thỏa mãn hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{{\rm{x}} + {\rm{y}} + 2 = 0}\\{{\rm{x}} - {\rm{y}} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = \frac{1}{2}}\\{{\rm{y}} = - \frac{5}{2}}\end{array}} \right.\)
Do đó tọa độ \(K\left( {\frac{1}{2}; - \frac{5}{2}} \right)\)
Ta có K là trung điểm NN’.
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_{{\rm{N'}}}} = 2{{\rm{x}}_{\rm{K}}} - {{\rm{x}}_{\rm{N}}} = 2.\frac{1}{2} + 2 = 3}\\{{{\rm{y}}_{{\rm{N'}}}} = 2{{\rm{y}}_{\rm{K}}} - {{\rm{y}}_{\rm{N}}} = 2.\left( { - \frac{5}{2}} \right) - 0 = - 5}\end{array}} \right.\)
Do đó tọa độ N’(3; –5).
Với R(1; –2), ta có \(\overrightarrow {N'R} = \left( { - 2;3} \right)\)
Đường thẳng \({\Delta _3}\) có vectơ chỉ phương \(\overrightarrow {N'R} = \left( { - 2;3} \right)\)
Suy ra \({\Delta _3}\) có vectơ pháp tuyến \({\vec n_{{\Delta _3}}} = \left( {3;2} \right)\)
Vậy đường thẳng \({\Delta _3}\) đi qua N’(3; –5) và nhận \({\vec n_{{\Delta _3}}} = \left( {3;2} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(3\left( {x{\rm{ }}-{\rm{ }}3} \right){\rm{ }} + {\rm{ }}2\left( {y{\rm{ }} + {\rm{ }}5} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 3x{\rm{ }} + {\rm{ }}2y{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0.\)
Giải bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Nội dung chi tiết bài 4 trang 19
Để giải quyết bài 4 trang 19 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Khái niệm hàm số: Định nghĩa, các loại hàm số (hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit,...).
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các yếu tố ảnh hưởng đến hình dạng đồ thị.
- Tính chất của hàm số: Tính đơn điệu, cực trị, giới hạn, liên tục.
- Ứng dụng của hàm số: Giải quyết các bài toán thực tế liên quan đến hàm số.
Lời giải chi tiết bài 4 trang 19
Dưới đây là lời giải chi tiết cho bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo. (Lưu ý: Nội dung lời giải cụ thể sẽ phụ thuộc vào đề bài của bài 4. Ví dụ minh họa dưới đây chỉ mang tính chất tham khảo.)
Ví dụ minh họa (Giả sử bài 4 yêu cầu vẽ đồ thị hàm số y = x2 - 4x + 3)
- Xác định các yếu tố của hàm số:
- Hàm số là hàm số bậc hai có dạng y = ax2 + bx + c, với a = 1, b = -4, c = 3.
- a > 0 nên hàm số có đồ thị là một parabol hướng lên.
- Đỉnh của parabol: x0 = -b/2a = 2; y0 = 22 - 4*2 + 3 = -1. Vậy đỉnh của parabol là (2, -1).
- Trục đối xứng của parabol: x = 2.
- Giao điểm với trục Oy: x = 0 => y = 3. Vậy giao điểm là (0, 3).
- Giao điểm với trục Ox: y = 0 => x2 - 4x + 3 = 0 => x = 1 hoặc x = 3. Vậy giao điểm là (1, 0) và (3, 0).
- Vẽ đồ thị hàm số:
Dựa vào các yếu tố đã xác định, ta có thể vẽ đồ thị hàm số y = x2 - 4x + 3.
Mẹo giải bài tập hàm số hiệu quả
Để giải các bài tập về hàm số một cách hiệu quả, bạn nên:
- Nắm vững các định nghĩa, tính chất và công thức liên quan đến hàm số.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị để kiểm tra kết quả.
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa và chuyên đề học tập Toán 11. Hãy truy cập tusach.vn để tìm kiếm lời giải cho các bài tập khác và nâng cao kiến thức của bạn!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 11 Chân trời sáng tạo | https://tusach.vn/toan-11-chan-troi-sang-tao |
| Chuyên đề học tập Toán 11 | https://tusach.vn/chuyen-de-toan-11 |