Giải mục 2 trang 32, 33, 34, 35 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 32, 33, 34, 35 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 32, 33, 34, 35 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài giải được trình bày rõ ràng, logic, kèm theo các lưu ý quan trọng để các em hiểu sâu sắc hơn về từng bước giải.
Gọi M’ và N’ lần lượt là ảnh của M và N qua phép vị tự V(O, k). Từ các hệ thức: \(\overrightarrow {OM'} = k\overrightarrow {OM} ,\overrightarrow {ON'} = k\overrightarrow {ON} ,\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \).
Khám phá 3
Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự \({V_{(O,{\rm{ }}k)}}.\) Cho biết \(\overrightarrow {BA} = m\overrightarrow {BC} \) hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) có bằng nhau không?
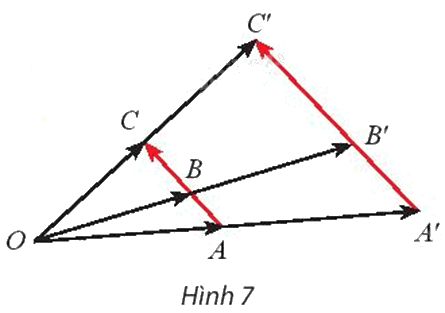
Phương pháp giải:
Chứng minh hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) cùng bằng vectơ thứ ba.
Lời giải chi tiết:
Theo bài, ta có A’, B’ lần lượt là ảnh của A, B qua \({V_{(O,{\rm{ }}k)}}.\)
Áp dụng tính chất 1, ta được \(\overrightarrow {B'A'} = k\overrightarrow {BA} \)
Chứng minh tương tự, ta được \(\overrightarrow {B'C'} = k\overrightarrow {BC} \)
Ta có \(\overrightarrow {B'A'} = k\overrightarrow {BA} = k.m\overrightarrow {BC} = m.k\overrightarrow {BC} = m\overrightarrow {B'C'} \)
Vậy hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) bằng nhau.
Thực hành 2
Cho tam giác ABC có G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, CA, AB.
a) Tìm phép vị tự biến tam giác ABC thành tam giác A’B’C’.
b) Chứng minh ba điểm H, G, O thẳng hàng.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
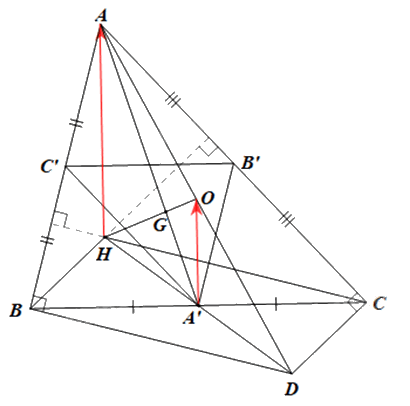
a) Để tìm phép vị tự biến ∆ABC thành ∆A’B’C’, ta tìm phép vị tự biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
∆ABC có A’ là trung điểm BC và G là trọng tâm.
Theo tính chất trọng tâm của tam giác, ta có \(\overrightarrow {AG} = 2\overrightarrow {GA'} \) hay \(\overrightarrow {GA'} = - \frac{1}{2}\overrightarrow {GA} \)
Suy ra A’ là ảnh của A qua \({V_{\left( {G, - \frac{1}{2}} \right)}}\)
Chứng minh tương tự, ta được \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( B \right) = B'\) và \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( C \right) = C'\)
Vậy \({V_{\left( {G, - \frac{1}{2}} \right)}}\) biến \(\Delta ABC\) thành
b) Gọi AD là đường kính của đường tròn tâm O ngoại tiếp ∆ABC.
Suy ra \(\widehat {ABD} = 90^\circ \) và O là trung điểm của AD.
Do đó \(\;AB{\rm{ }} \bot {\rm{ }}BD.\)
Mà \(CH \bot AB\) (do H là trực tâm của ∆ABC).
Vì vậy BD // CH.
Chứng minh tương tự, ta được BH // CD.
Suy ra tứ giác BHCD là hình bình hành.
Mà A’ là trung điểm BC (giả thiết).
Do đó A’ cũng là trung điểm của DH.
∆ADH có A’O là đường trung bình của tam giác nên \(A'O = \frac{1}{2}HA\) và
Suy ra \(\overrightarrow {A'O} = \frac{1}{2}\overrightarrow {HA} = - \frac{1}{2}\overrightarrow {AH} \)
Ta có \(\overrightarrow {GO} = \overrightarrow {GA'} + \overrightarrow {A'O} = - \frac{1}{2}\overrightarrow {GA} - \frac{1}{2}\overrightarrow {AH} \) \( = - \frac{1}{2}\left( {\overrightarrow {GA} + \overrightarrow {AH} } \right) = - \frac{1}{2}\overrightarrow {GH} \)
Khi đó \(\overrightarrow {GO} \) và \(\overrightarrow {GH} \) cùng phương nên ba điểm G, H, O thẳng hàng.
Vậy ba điểm G, H, O thẳng hàng.
Khám phá 2
Gọi M’ và N’ lần lượt là ảnh của M và N qua phép vị tự V(O, k). Từ các hệ thức: \(\overrightarrow {OM'} = k\overrightarrow {OM} ,\overrightarrow {ON'} = k\overrightarrow {ON} ,\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \). Biểu thị vectơ \(\overrightarrow {M'N'} \) theo vectơ \(\overrightarrow {MN} .\)
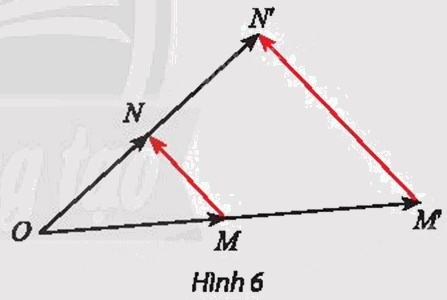
Phương pháp giải:
Sử dụng quy tắc hiệu để biểu diễn
Lời giải chi tiết:
Ta có \(\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \)′
\( = k\overrightarrow {ON} - k\overrightarrow {OM} = k\left( {\overrightarrow {ON} - \overrightarrow {OM} } \right) = k\overrightarrow {MN} \).
Vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \)
Vận dụng 2
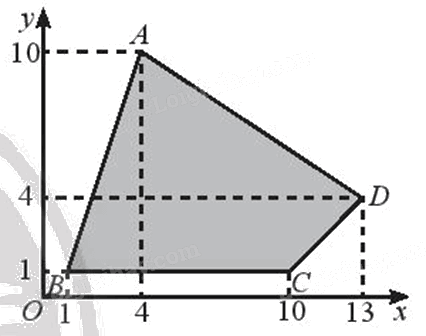
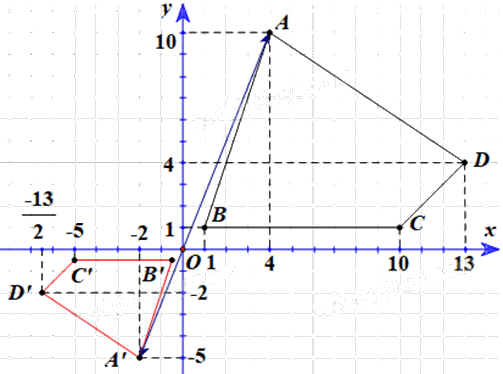
Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, - \frac{1}{2}} \right)}}\).
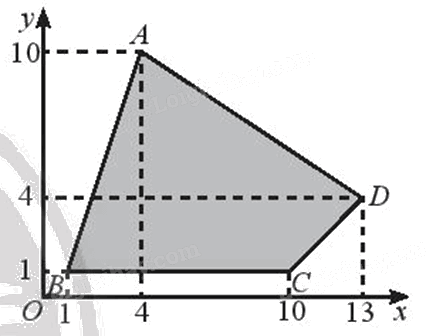
Phương pháp giải:
Để tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, - \frac{1}{2}} \right)}}\) ta tìm ảnh của từng điểm A, B, C, D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\). Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
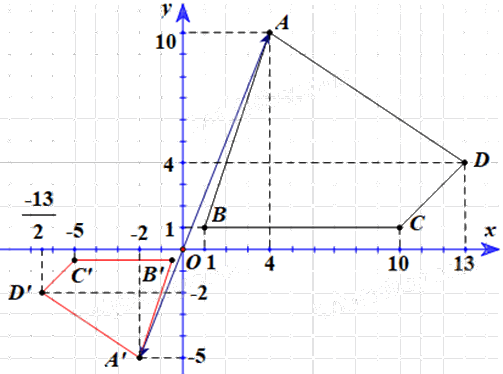
Để tìm ảnh của tứ giác ABCD qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\), ta tìm ảnh của các điểm A, B, C, D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\).
Quan sát hình vẽ, ta thấy \(\;A\left( {4;{\rm{ }}10} \right),{\rm{ }}B\left( {1;{\rm{ }}1} \right),{\rm{ }}C\left( {10;{\rm{ }}1} \right),{\rm{ }}D\left( {13;{\rm{ }}4} \right).\)
⦁ Đặt là ảnh của A qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {O{A'}} = - \frac{1}{2}\overrightarrow {OA} \) với \(\overrightarrow {OA} = \left( {4;10} \right)\) và \(\overrightarrow {O{A'}} = \left( {{x_{A'}};{y_{A'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{A'}} = - \frac{1}{2}.4 = - 2\\{y_{A'}} = - \frac{1}{2}.10 = - 5\end{array} \right.\)
Vì vậy tọa độ
⦁ Đặt \(B'\left( {{x_{B'}};{y_{B'}}} \right)\) là ảnh của B qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {O{B'}} = - \frac{1}{2}\overrightarrow {OB} \) với \(\overrightarrow {OB} = \left( {1;1} \right)\) và \(\overrightarrow {O{B'}} = \left( {{x_{B'}};{y_{B'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{B'}} = - \frac{1}{2}.1 = - \frac{1}{2}\\{y_{B'}} = - \frac{1}{2}.1 = - \frac{1}{2}\end{array} \right.\)
Vì vậy tọa độ \(B'\left( { - \frac{1}{2}; - \frac{1}{2}} \right)\)
⦁ Đặt \(C'\left( {{x_{C'}};{y_{C'}}} \right)\) là ảnh của C qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {OC'} = - \frac{1}{2}\overrightarrow {OC} \) với \(\overrightarrow {OC} = \left( {10;1} \right)\) và \(\overrightarrow {OC'} = \left( {{x_{C'}};{y_{C'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{C'}} = - \frac{1}{2}.10 = - 5\\{y_{C'}} = - \frac{1}{2}.1 = - \frac{1}{2}\end{array} \right.\)
Vì vậy tọa độ \(C'\left( { - 5; - \frac{1}{2}} \right)\)
⦁ Đặt \(D' = \left( {{x_{D'}};{y_{D'}}} \right)\) là ảnh của D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {OD'} = - \frac{1}{2}\overrightarrow {OD} \)với \(\overrightarrow {OD} = \left( {13;4} \right)\) và \(\overrightarrow {O{D'}} = \left( {{x_{D'}};{y_{D'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{D'}} = - \frac{1}{2}.13 = - \frac{{13}}{2}\\{y_{D'}} = - \frac{1}{2}.4 = - 2\end{array} \right.\)
Vì vậy tọa độ \(D'\left( { - \frac{{13}}{2}; - 2} \right)\)
Vậy ảnh của tứ giác ABCD qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\) là tứ giác A’B’C’D’ có tọa độ các đỉnh là \(A'\left( {-2;{\rm{ }}-5} \right),B'\left( { - \frac{1}{2}; - \frac{1}{2}} \right),C'\left( { - 5; - \frac{1}{2}} \right),D'\left( { - \frac{{13}}{2}; - 2} \right)\)
- Khám phá 2
- Khám phá 3
- Thực hành 2
- Khám phá 4
- Vận dụng 2
Gọi M’ và N’ lần lượt là ảnh của M và N qua phép vị tự V(O, k). Từ các hệ thức: \(\overrightarrow {OM'} = k\overrightarrow {OM} ,\overrightarrow {ON'} = k\overrightarrow {ON} ,\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \). Biểu thị vectơ \(\overrightarrow {M'N'} \) theo vectơ \(\overrightarrow {MN} .\)
Phương pháp giải:
Sử dụng quy tắc hiệu để biểu diễn
Lời giải chi tiết:
Ta có \(\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \)′
\( = k\overrightarrow {ON} - k\overrightarrow {OM} = k\left( {\overrightarrow {ON} - \overrightarrow {OM} } \right) = k\overrightarrow {MN} \).
Vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \)
Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự \({V_{(O,{\rm{ }}k)}}.\) Cho biết \(\overrightarrow {BA} = m\overrightarrow {BC} \) hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) có bằng nhau không?
Phương pháp giải:
Chứng minh hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) cùng bằng vectơ thứ ba.
Lời giải chi tiết:
Theo bài, ta có A’, B’ lần lượt là ảnh của A, B qua \({V_{(O,{\rm{ }}k)}}.\)
Áp dụng tính chất 1, ta được \(\overrightarrow {B'A'} = k\overrightarrow {BA} \)
Chứng minh tương tự, ta được \(\overrightarrow {B'C'} = k\overrightarrow {BC} \)
Ta có \(\overrightarrow {B'A'} = k\overrightarrow {BA} = k.m\overrightarrow {BC} = m.k\overrightarrow {BC} = m\overrightarrow {B'C'} \)
Vậy hai vectơ \(\overrightarrow {B'A'} \) và \(m\overrightarrow {B'C'} \) bằng nhau.
Cho tam giác ABC có G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, CA, AB.
a) Tìm phép vị tự biến tam giác ABC thành tam giác A’B’C’.
b) Chứng minh ba điểm H, G, O thẳng hàng.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
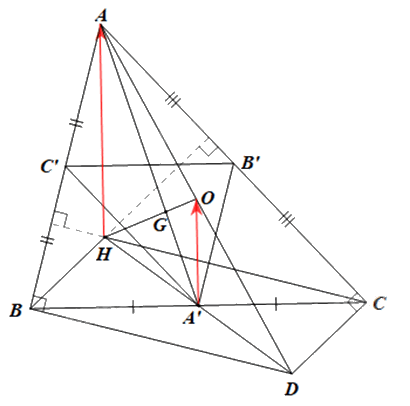
a) Để tìm phép vị tự biến ∆ABC thành ∆A’B’C’, ta tìm phép vị tự biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
∆ABC có A’ là trung điểm BC và G là trọng tâm.
Theo tính chất trọng tâm của tam giác, ta có \(\overrightarrow {AG} = 2\overrightarrow {GA'} \) hay \(\overrightarrow {GA'} = - \frac{1}{2}\overrightarrow {GA} \)
Suy ra A’ là ảnh của A qua \({V_{\left( {G, - \frac{1}{2}} \right)}}\)
Chứng minh tương tự, ta được \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( B \right) = B'\) và \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( C \right) = C'\)
Vậy \({V_{\left( {G, - \frac{1}{2}} \right)}}\) biến \(\Delta ABC\) thành
b) Gọi AD là đường kính của đường tròn tâm O ngoại tiếp ∆ABC.
Suy ra \(\widehat {ABD} = 90^\circ \) và O là trung điểm của AD.
Do đó \(\;AB{\rm{ }} \bot {\rm{ }}BD.\)
Mà \(CH \bot AB\) (do H là trực tâm của ∆ABC).
Vì vậy BD // CH.
Chứng minh tương tự, ta được BH // CD.
Suy ra tứ giác BHCD là hình bình hành.
Mà A’ là trung điểm BC (giả thiết).
Do đó A’ cũng là trung điểm của DH.
∆ADH có A’O là đường trung bình của tam giác nên \(A'O = \frac{1}{2}HA\) và
Suy ra \(\overrightarrow {A'O} = \frac{1}{2}\overrightarrow {HA} = - \frac{1}{2}\overrightarrow {AH} \)
Ta có \(\overrightarrow {GO} = \overrightarrow {GA'} + \overrightarrow {A'O} = - \frac{1}{2}\overrightarrow {GA} - \frac{1}{2}\overrightarrow {AH} \) \( = - \frac{1}{2}\left( {\overrightarrow {GA} + \overrightarrow {AH} } \right) = - \frac{1}{2}\overrightarrow {GH} \)
Khi đó \(\overrightarrow {GO} \) và \(\overrightarrow {GH} \) cùng phương nên ba điểm G, H, O thẳng hàng.
Vậy ba điểm G, H, O thẳng hàng.
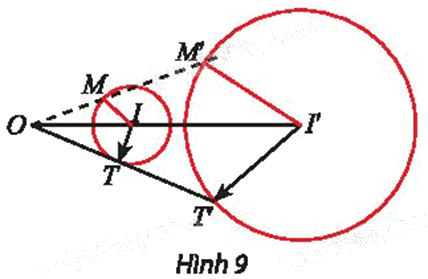
Cho phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}\) và đường tròn (C) tâm I bán kính r. Xét điểm M thuộc (C), gọi I’ và M’ là ảnh của I và M qua phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}.\)
a) Tính I’M’ theo r và k.
b) Khi cho điểm M chạy trên đường tròn (C) thì M’ chạy trên đường nào?
Phương pháp giải:
Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|, biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng |k|, biến đường tròn bán kính r thành đường tròn bán kính \(r' = |k|.r\).
Lời giải chi tiết:
a) Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( I \right){\rm{ }} = {\rm{ }}I'\) và \({V_{\left( {O,{\rm{ }}k} \right)}}\left( M \right){\rm{ }} = {\rm{ }}M'.\)
Suy ra \(I'M'{\rm{ }} = {\rm{ }}\left| k \right|.IM{\rm{ }} = {\rm{ }}\left| k \right|.r.\)
Vậy
b) Theo đề, ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\;\) biến điểm M thành điểm M’.
Vậy khi M chạy trên đường tròn (C) thì M’ chạy trên đường tròn (C’) có tâm I’, bán kính \(r'{\rm{ }} = {\rm{ }}\left| k \right|.r\) là ảnh của (C) qua \({V_{\left( {O,{\rm{ }}k} \right)}}.\)
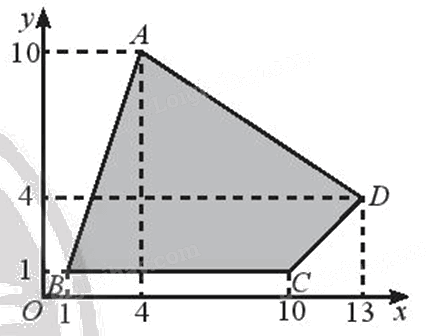
Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, - \frac{1}{2}} \right)}}\).
Phương pháp giải:
Để tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, - \frac{1}{2}} \right)}}\) ta tìm ảnh của từng điểm A, B, C, D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\). Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
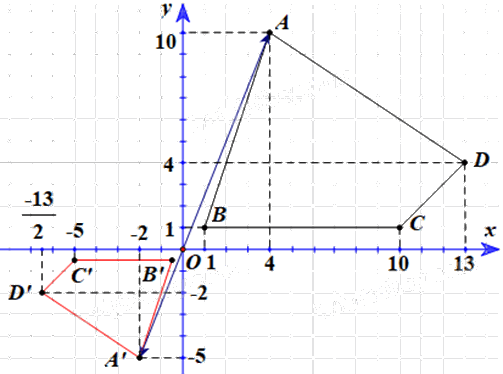
Để tìm ảnh của tứ giác ABCD qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\), ta tìm ảnh của các điểm A, B, C, D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\).
Quan sát hình vẽ, ta thấy \(\;A\left( {4;{\rm{ }}10} \right),{\rm{ }}B\left( {1;{\rm{ }}1} \right),{\rm{ }}C\left( {10;{\rm{ }}1} \right),{\rm{ }}D\left( {13;{\rm{ }}4} \right).\)
⦁ Đặt là ảnh của A qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {O{A'}} = - \frac{1}{2}\overrightarrow {OA} \) với \(\overrightarrow {OA} = \left( {4;10} \right)\) và \(\overrightarrow {O{A'}} = \left( {{x_{A'}};{y_{A'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{A'}} = - \frac{1}{2}.4 = - 2\\{y_{A'}} = - \frac{1}{2}.10 = - 5\end{array} \right.\)
Vì vậy tọa độ
⦁ Đặt \(B'\left( {{x_{B'}};{y_{B'}}} \right)\) là ảnh của B qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {O{B'}} = - \frac{1}{2}\overrightarrow {OB} \) với \(\overrightarrow {OB} = \left( {1;1} \right)\) và \(\overrightarrow {O{B'}} = \left( {{x_{B'}};{y_{B'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{B'}} = - \frac{1}{2}.1 = - \frac{1}{2}\\{y_{B'}} = - \frac{1}{2}.1 = - \frac{1}{2}\end{array} \right.\)
Vì vậy tọa độ \(B'\left( { - \frac{1}{2}; - \frac{1}{2}} \right)\)
⦁ Đặt \(C'\left( {{x_{C'}};{y_{C'}}} \right)\) là ảnh của C qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {OC'} = - \frac{1}{2}\overrightarrow {OC} \) với \(\overrightarrow {OC} = \left( {10;1} \right)\) và \(\overrightarrow {OC'} = \left( {{x_{C'}};{y_{C'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{C'}} = - \frac{1}{2}.10 = - 5\\{y_{C'}} = - \frac{1}{2}.1 = - \frac{1}{2}\end{array} \right.\)
Vì vậy tọa độ \(C'\left( { - 5; - \frac{1}{2}} \right)\)
⦁ Đặt \(D' = \left( {{x_{D'}};{y_{D'}}} \right)\) là ảnh của D qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\)
Suy ra \(\overrightarrow {OD'} = - \frac{1}{2}\overrightarrow {OD} \)với \(\overrightarrow {OD} = \left( {13;4} \right)\) và \(\overrightarrow {O{D'}} = \left( {{x_{D'}};{y_{D'}}} \right)\)
Do đó \(\left\{ \begin{array}{l}{x_{D'}} = - \frac{1}{2}.13 = - \frac{{13}}{2}\\{y_{D'}} = - \frac{1}{2}.4 = - 2\end{array} \right.\)
Vì vậy tọa độ \(D'\left( { - \frac{{13}}{2}; - 2} \right)\)
Vậy ảnh của tứ giác ABCD qua \({V_{\left( {O, - \frac{1}{2}} \right)}}\) là tứ giác A’B’C’D’ có tọa độ các đỉnh là \(A'\left( {-2;{\rm{ }}-5} \right),B'\left( { - \frac{1}{2}; - \frac{1}{2}} \right),C'\left( { - 5; - \frac{1}{2}} \right),D'\left( { - \frac{{13}}{2}; - 2} \right)\)
Khám phá 4
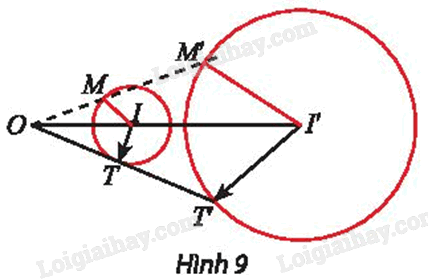
Cho phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}\) và đường tròn (C) tâm I bán kính r. Xét điểm M thuộc (C), gọi I’ và M’ là ảnh của I và M qua phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}.\)
a) Tính I’M’ theo r và k.
b) Khi cho điểm M chạy trên đường tròn (C) thì M’ chạy trên đường nào?
Phương pháp giải:
Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|, biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng |k|, biến đường tròn bán kính r thành đường tròn bán kính \(r' = |k|.r\).
Lời giải chi tiết:
a) Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( I \right){\rm{ }} = {\rm{ }}I'\) và \({V_{\left( {O,{\rm{ }}k} \right)}}\left( M \right){\rm{ }} = {\rm{ }}M'.\)
Suy ra \(I'M'{\rm{ }} = {\rm{ }}\left| k \right|.IM{\rm{ }} = {\rm{ }}\left| k \right|.r.\)
Vậy
b) Theo đề, ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\;\) biến điểm M thành điểm M’.
Vậy khi M chạy trên đường tròn (C) thì M’ chạy trên đường tròn (C’) có tâm I’, bán kính \(r'{\rm{ }} = {\rm{ }}\left| k \right|.r\) là ảnh của (C) qua \({V_{\left( {O,{\rm{ }}k} \right)}}.\)
Giải mục 2 trang 32, 33, 34, 35 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề. Việc giải các bài tập trong mục này không chỉ giúp củng cố lý thuyết mà còn rèn luyện khả năng vận dụng kiến thức vào thực tế.
Nội dung chính của Mục 2 (trang 32, 33, 34, 35)
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định chính xác nội dung mà nó đề cập đến. Thông thường, đây có thể là một chương về:
- Hàm số lượng giác: Các khái niệm về hàm số lượng giác, đồ thị, tính chất và ứng dụng.
- Phương trình lượng giác: Các phương pháp giải phương trình lượng giác cơ bản và nâng cao.
- Đạo hàm: Khái niệm đạo hàm, các quy tắc tính đạo hàm và ứng dụng trong việc giải quyết các bài toán tối ưu.
- Giới hạn: Khái niệm giới hạn, các tính chất và ứng dụng trong việc tính toán.
Hướng dẫn giải chi tiết các bài tập trang 32, 33, 34, 35
Dưới đây là hướng dẫn giải chi tiết cho một số bài tập tiêu biểu trong Mục 2, trang 32, 33, 34, 35:
Bài tập 1 (Trang 32):
(Giả sử bài tập là về hàm số lượng giác)
Đề bài: Tìm tập xác định của hàm số y = √(2 - cosx).
Lời giải:
- Để hàm số xác định, điều kiện là 2 - cosx ≥ 0.
- ⇔ cosx ≤ 2.
- Vì -1 ≤ cosx ≤ 1 với mọi x, nên cosx ≤ 2 luôn đúng.
- Vậy tập xác định của hàm số là R.
Bài tập 2 (Trang 33):
(Giả sử bài tập là về phương trình lượng giác)
Đề bài: Giải phương trình sin2x = 1.
Lời giải:
- 2x = π/2 + k2π (k ∈ Z)
- x = π/4 + kπ (k ∈ Z)
Lưu ý quan trọng khi giải bài tập
Để giải bài tập Toán 11 Chân trời sáng tạo một cách hiệu quả, các em cần lưu ý những điều sau:
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, tính chất và công thức liên quan đến chủ đề đang học.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị có thể giúp các em giải quyết bài tập nhanh chóng và chính xác hơn.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp những lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 11 Chân trời sáng tạo. Chúng tôi hy vọng rằng với sự hỗ trợ của Tusach.vn, các em sẽ học tập hiệu quả hơn và đạt được kết quả tốt nhất.
Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!