Giải mục 2 trang 54, 55, 56, 57, 58 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 54-58 Toán 11 Chuyên đề học tập - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 54, 55, 56, 57, 58 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của tusach.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
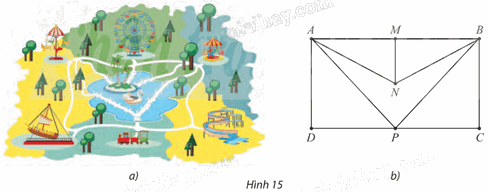
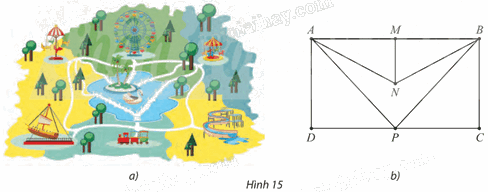
Đồ thị ở Hình 15b biểu diễn các điểm vui chơi trong một công viên với những con đường nối giữa chúng như Hình 15a.
Khám phá 4
Đồ thị ở Hình 15b biểu diễn các điểm vui chơi trong một công viên với những con đường nối giữa chúng như Hình 15a. Có thể đi theo những con đường này để thăm tất cả các điểm vui chơi mỗi điểm đúng một lần hay không? Nếu có, chỉ ra ít nhất một đường đi như vậy.
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Ta có thể đi theo những con đường này để thăm tất cả các điểm vui chơi mỗi điểm đúng một lần.
Chẳng hạn, ta có thể đi theo một số đường đi như sau: ANMBCPD, NBMADPC, DANMBCP,…
Thực hành 3
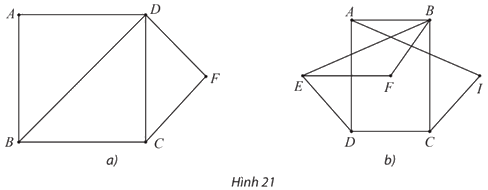
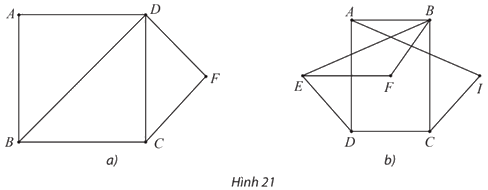
Hãy chỉ ra rằng mỗi đồ thị sau đây có chu trình Hamilton.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết:
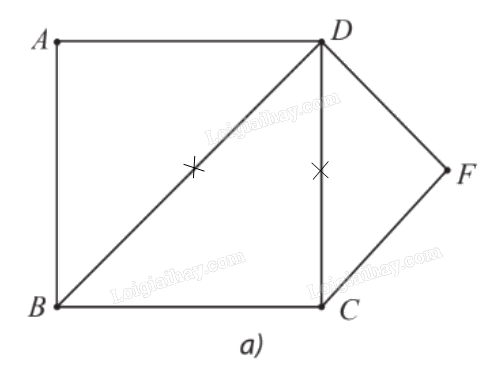
⦁ Hình 21a:
Đồ thị ở Hình 21a có các đỉnh A, F có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh AB, AD, FD, FC trong đồ thị ở Hình 21a.
Do đó h không thể đi qua các cạnh BD, DC.
Nếu xóa đi hai cạnh này thì đỉnh B, C trở thành có bậc 2.
Vì vậy h phải đi qua cạnh BC.
Khi đó ta được chu trình Hamilton h: ADFCBA.
⦁ Hình 21b:
Đồ thị ở Hình 21b có các đỉnh F, I có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh FE, FB, IA, IC.
Do đó ta được chu trình Hamilton h: AICBFEDA (hoặc AICDEFBA).
Vậy cả hai đồ thị đã cho đều có chu trình Hamilton.
Vận dụng 2
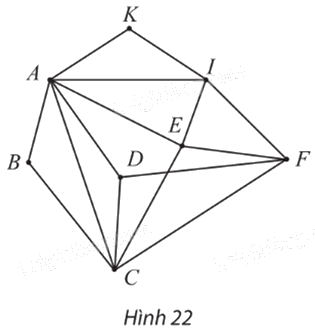
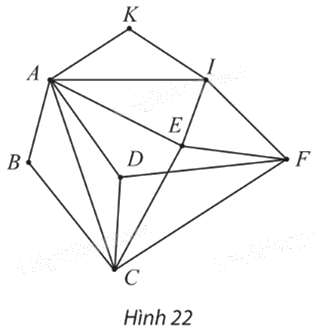
Các đỉnh của đồ thị ở Hình 22 biểu thị các điểm du lịch trong một thành phố, các cạnh biểu thị đường đi giữa các điểm du lịch này. Có hay không một cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch?
Phương pháp giải:
Kiểm tra xem đường đi có là chu trình Hamilton không.
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần. Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết:
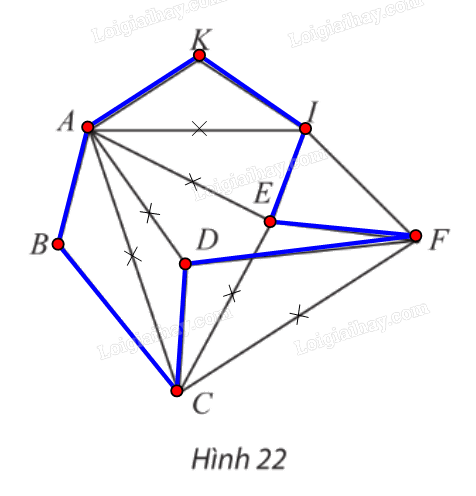
Đồ thị ở Hình 22 có các đỉnh B, K có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi các các cạnh AB, BC, AK, KI.
Do đó h không thể đi qua các cạnh AI, AD, AD, AE.
Nếu xóa đi bốn cạnh trên thì các đỉnh A, D trở thành bậc 2.
Suy ra h phải đi qua các cạnh AB, AK, DC, DF.
Do đó h không thể đi qua các cạnh CE, CF.
Nếu xóa đi thêm hai cạnh trên thì đỉnh E trở thành bậc 2.
Suy ra h phải đi qua các cạnh EI, EF.
Vì vậy ta được chu trình Hamilton h: ABCDFEIKA.
Vậy có cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch.
- Khám phá 4
- Thực hành 3
- Vận dụng 2
Đồ thị ở Hình 15b biểu diễn các điểm vui chơi trong một công viên với những con đường nối giữa chúng như Hình 15a. Có thể đi theo những con đường này để thăm tất cả các điểm vui chơi mỗi điểm đúng một lần hay không? Nếu có, chỉ ra ít nhất một đường đi như vậy.
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Ta có thể đi theo những con đường này để thăm tất cả các điểm vui chơi mỗi điểm đúng một lần.
Chẳng hạn, ta có thể đi theo một số đường đi như sau: ANMBCPD, NBMADPC, DANMBCP,…
Hãy chỉ ra rằng mỗi đồ thị sau đây có chu trình Hamilton.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết:
⦁ Hình 21a:
Đồ thị ở Hình 21a có các đỉnh A, F có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh AB, AD, FD, FC trong đồ thị ở Hình 21a.
Do đó h không thể đi qua các cạnh BD, DC.
Nếu xóa đi hai cạnh này thì đỉnh B, C trở thành có bậc 2.
Vì vậy h phải đi qua cạnh BC.
Khi đó ta được chu trình Hamilton h: ADFCBA.
⦁ Hình 21b:
Đồ thị ở Hình 21b có các đỉnh F, I có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh FE, FB, IA, IC.
Do đó ta được chu trình Hamilton h: AICBFEDA (hoặc AICDEFBA).
Vậy cả hai đồ thị đã cho đều có chu trình Hamilton.
Các đỉnh của đồ thị ở Hình 22 biểu thị các điểm du lịch trong một thành phố, các cạnh biểu thị đường đi giữa các điểm du lịch này. Có hay không một cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch?
Phương pháp giải:
Kiểm tra xem đường đi có là chu trình Hamilton không.
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần. Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết:
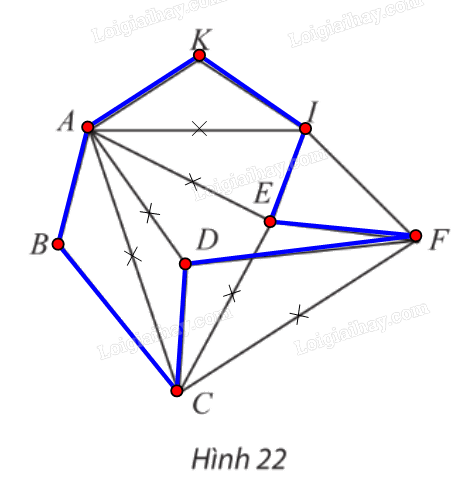
Đồ thị ở Hình 22 có các đỉnh B, K có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi các các cạnh AB, BC, AK, KI.
Do đó h không thể đi qua các cạnh AI, AD, AD, AE.
Nếu xóa đi bốn cạnh trên thì các đỉnh A, D trở thành bậc 2.
Suy ra h phải đi qua các cạnh AB, AK, DC, DF.
Do đó h không thể đi qua các cạnh CE, CF.
Nếu xóa đi thêm hai cạnh trên thì đỉnh E trở thành bậc 2.
Suy ra h phải đi qua các cạnh EI, EF.
Vì vậy ta được chu trình Hamilton h: ABCDFEIKA.
Vậy có cách đi tham quan tất cả các điểm du lịch của thành phố, mỗi điểm qua đúng một lần, xuất phát và kết thúc tại cùng một điểm du lịch.
Giải mục 2 trang 54-58 Toán 11 Chuyên đề học tập - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt vào giải bài tập. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để đạt kết quả cao trong các bài kiểm tra và thi cử.
Nội dung chính của Mục 2 (trang 54-58)
Để giúp các em hiểu rõ hơn về nội dung Mục 2, chúng ta sẽ cùng nhau phân tích các phần chính:
- Lý thuyết trọng tâm: Tóm tắt các định nghĩa, định lý, công thức quan trọng liên quan đến chủ đề.
- Ví dụ minh họa: Phân tích chi tiết các ví dụ điển hình, giúp các em hiểu cách áp dụng lý thuyết vào thực tế.
- Bài tập luyện tập: Cung cấp các bài tập với mức độ khó tăng dần, từ dễ đến khó, để các em rèn luyện kỹ năng giải toán.
Giải chi tiết các bài tập trang 54
Bài 1: (Đề bài)...
Lời giải: (Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan). Ví dụ: Để giải bài này, ta sử dụng công thức... Bước 1: ... Bước 2: ... Bước 3: ... Kết luận: ...
Giải chi tiết các bài tập trang 55
Bài 2: (Đề bài)...
Lời giải: (Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan).
Giải chi tiết các bài tập trang 56
Bài 3: (Đề bài)...
Lời giải: (Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan).
Giải chi tiết các bài tập trang 57
Bài 4: (Đề bài)...
Lời giải: (Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan).
Giải chi tiết các bài tập trang 58
Bài 5: (Đề bài)...
Lời giải: (Giải thích chi tiết từng bước, kèm theo các công thức và định lý liên quan).
Lưu ý: Trong quá trình giải bài tập, các em nên chú ý đến các điều kiện của bài toán và kiểm tra lại kết quả để đảm bảo tính chính xác.
Mẹo học tập hiệu quả
- Đọc kỹ lý thuyết: Nắm vững các định nghĩa, định lý, công thức trước khi bắt đầu giải bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Hỏi thầy cô hoặc bạn bè: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô hoặc bạn bè để được giúp đỡ.
- Sử dụng các nguồn tài liệu tham khảo: Tham khảo thêm các sách giáo khoa, tài liệu tham khảo, hoặc các trang web học tập trực tuyến.
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn trong việc học tập và đạt kết quả tốt nhất trong môn Toán 11. Chúc các em học tốt!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 54 | Dễ |
| Bài 2 | 55 | Trung bình |
| Bài 3 | 56 | Khó |