Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của các bạn.

Tìm các tỉ số vị tự của phép biến hình được thực hiện trên cây thước vẽ truyền trong Hình 13.

Đề bài

Tìm các tỉ số vị tự của phép biến hình được thực hiện trên cây thước vẽ truyền trong Hình 13.

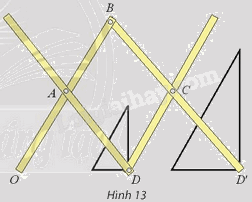
Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo 2

Quan sát hình vẽ và sử dụng hệ quả:

Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|, biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng |k|, biến đường tròn bán kính r thành đường tròn bán kính \(r' = |k|.r\).

Lời giải chi tiết

Xét hình tam giác đỉnh D khi vẽ truyền cho ta hình tam giác đỉnh D’ là ảnh của hình D.

Ta có ba điểm O, D, D’ thẳng hàng nên \(\overrightarrow {OD'} = k\overrightarrow {OD} \).

Do đó \(\;{V_{(O,{\rm{ }}k)}}\left( D \right){\rm{ }} = {\rm{ }}D'\) và \(OD'{\rm{ }} = {\rm{ }}\left| k \right|.OD.\)

Vì D, D’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0.\)

Suy ra \(k = \frac{{OD'}}{{OD}}\)

Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).

Khi đó áp dụng định lí Thales, ta được \(k = \frac{{OD}}{{OD'}} = \frac{{OA}}{{OB}}\)

Vậy phép vị tự biến hình tam giác có đỉnh D thành tam giác có đỉnh D’ là \({V_{\left( {O,\frac{{OA}}{{OB}}} \right)}}\)

Ngược lại, phép vị tự biến hình tam giác đỉnh D’ khi vẽ truyền cho ta hình tam giác đỉnh D là ảnh của hình D là \({V_{\left( {O,\frac{{OB}}{{OA}}} \right)}}\)

Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp giải

Bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải tính đạo hàm, tìm cực trị, và khảo sát sự biến thiên của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức liên quan đến đạo hàm, đồng thời rèn luyện kỹ năng giải toán một cách thành thạo.

Nội dung chi tiết bài 7 trang 36

Bài 7 thường xoay quanh các dạng bài sau:

Dạng 1: Tính đạo hàm của hàm số.
Dạng 2: Tìm cực trị của hàm số.
Dạng 3: Khảo sát sự biến thiên của hàm số.
Dạng 4: Ứng dụng đạo hàm để giải các bài toán tối ưu.

Lời giải chi tiết bài 7 trang 36 (Ví dụ minh họa)

Đề bài: (Giả sử đề bài cụ thể ở đây) Cho hàm số y = f(x) = x³ - 3x² + 2. Hãy tìm cực đại, cực tiểu của hàm số.

Giải:

Bước 1: Tính đạo hàm cấp 1: f'(x) = 3x² - 6x
Bước 2: Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
Bước 3: Lập bảng biến thiên:
x -∞ 0 2 +∞
f'(x) + - +
f(x) NB ĐC TC
Bước 4: Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	NB	ĐC	TC

Mẹo giải bài tập đạo hàm hiệu quả

Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:

Nắm vững các công thức đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng bảng biến thiên để khảo sát sự biến thiên của hàm số.
Kiểm tra lại kết quả sau khi giải xong.

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập Toán 11 Chân trời sáng tạo. Chúng tôi hy vọng rằng với những hướng dẫn này, các bạn sẽ tự tin hơn trong việc giải các bài tập và đạt kết quả tốt trong học tập. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!

Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi. Chúc các bạn học tập tốt!

Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp giải

Nội dung chi tiết bài 7 trang 36

Lời giải chi tiết bài 7 trang 36 (Ví dụ minh họa)

Mẹo giải bài tập đạo hàm hiệu quả

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN