Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 10 trang 41 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúng tôi sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán hiệu quả.

Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.

Cho đường tròn (O; R) và điểm I cố định khác O. Vẽ điểm M tùy ý trên (O). Tia phân giác của góc MOI cắt IM tại N. Điểm N di động trên đường nào khi M di động trên (O)?

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo 1

Vẽ hình, dựa vào phép vị tự, suy luận để chứng minh

Lời giải chi tiết

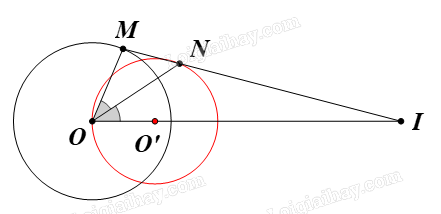
Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo 2

Đặt \(IO{\rm{ }} = {\rm{ }}d{\rm{ }}\left( {d{\rm{ }} \ne {\rm{ }}0} \right).\)

∆MOI có ON là đường phân giác, áp dụng tính chất đường phân giác, ta được: \(\frac{{NM}}{{NI}} = \frac{{OM}}{{OI}} = \frac{R}{d}\)

Suy ra \(\frac{{NM}}{{NI}} + 1 = \frac{R}{d} + 1\)

Khi đó \(\frac{{NM + NI}}{{NI}} = \frac{{R + d}}{d}\)

Vì vậy \(\frac{{IM}}{{NI}} = \frac{{R + d}}{d}\)

Suy ra \(\frac{{IN}}{{IM}} = \frac{d}{{R + d}}\)

Do đó \(IN = \frac{d}{{R + d}}.IM\)

Vì vậy \(\overrightarrow {IN} = \frac{d}{{R + d}}.\overrightarrow {IM} \) (do \(\overrightarrow {IN} ,\overrightarrow {IM} \) cùng hướng).

Khi đó phép vị tự tâm I, tỉ số \(k = \frac{d}{{R + d}}\) biến điểm M thành điểm N.

Giả sử khi M ở vị trí sao cho ba điểm O, M, I thẳng hàng (tức là, \(\widehat {IOM} = 0^\circ \) )thì tia phân giác của góc MOI không thể cắt IM tại N.

Tức là, điểm N không tồn tại.

Ta đặt \({M'_0} = {V_{\left( {I,\frac{d}{{R + d}}} \right)}}\left( {{M_0}} \right)\), với M₀ là điểm nằm trên đường tròn (O; R) sao cho ba điểm \(O,{\rm{ }}{M_0},{\rm{ }}I\) thẳng hàng.

Vậy khi M chạy trên đường tròn (O; R) sao cho ba điểm O, M, I không thẳng hàng thì N chạy trên một đường tròn \(\left( {O';{\rm{ }}R'} \right)\) cố định là ảnh của đường tròn (O; R) qua phép vị tự tâm I, tỉ số \(k = \frac{d}{{R + d}}\) sao cho \(\;N{\rm{ }} \ne {\rm{ }}{M_0},\) với M₀ là điểm nằm trên đường tròn (O; R) sao cho ba điểm \(O,{\rm{ }}{M_0},{\rm{ }}I\) thẳng hàng

Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan

Bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung chi tiết bài 10 trang 41

Bài 10 thường bao gồm các dạng bài tập sau:

Dạng 1: Tính đạo hàm của hàm số: Học sinh cần áp dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của các hàm số phức tạp.
Dạng 2: Tìm cực trị của hàm số: Sử dụng đạo hàm để xác định các điểm cực trị (cực đại, cực tiểu) của hàm số.
Dạng 3: Khảo sát hàm số: Phân tích sự biến thiên của hàm số dựa trên đạo hàm, xác định khoảng đồng biến, nghịch biến, và các điểm cực trị.
Dạng 4: Ứng dụng đạo hàm vào các bài toán thực tế: Giải quyết các bài toán liên quan đến tối ưu hóa, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trong các tình huống thực tế.

Lời giải chi tiết bài 10 trang 41 (Ví dụ)

Bài toán: (Giả sử đây là một bài toán mẫu) Cho hàm số y = x³ - 3x² + 2. Tìm cực đại và cực tiểu của hàm số.

Lời giải:

Bước 1: Tính đạo hàm: y' = 3x² - 6x
Bước 2: Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
Bước 3: Xác định loại cực trị:
- Với x < 0, y' > 0, hàm số đồng biến.
- Với 0 < x < 2, y' < 0, hàm số nghịch biến.
- Với x > 2, y' > 0, hàm số đồng biến.
Vậy, hàm số đạt cực đại tại x = 0, y_max = 2 và đạt cực tiểu tại x = 2, y_min = -2.

Mẹo giải bài tập hiệu quả

Để giải bài tập về đạo hàm hiệu quả, bạn nên:

Nắm vững các quy tắc tính đạo hàm.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng sơ đồ hoặc bảng biến thiên để phân tích sự biến thiên của hàm số.
Kiểm tra lại kết quả sau khi giải xong.

Tài liệu tham khảo hữu ích

Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11
Các trang web học Toán trực tuyến
Các video hướng dẫn giải bài tập Toán 11

Kết luận

Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, bạn sẽ tự tin hơn khi giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúc bạn học tốt!

Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 10 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan

Nội dung chi tiết bài 10 trang 41

Lời giải chi tiết bài 10 trang 41 (Ví dụ)

Mẹo giải bài tập hiệu quả

Tài liệu tham khảo hữu ích

Kết luận

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN