Giải bài 2 trang 46, 47, 48 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 2 trang 46, 47, 48 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 2 thuộc chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, cùng với các bước giải chi tiết, giúp các em học sinh dễ dàng tiếp thu và áp dụng vào thực tế.
Đồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng)
Vận dụng 2
Có hay không một đồ thị có ba đỉnh, trong đó hai đỉnh có bậc bằng 2 và một đỉnh có bậc bằng 3?
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Không có, vì tổng tất cả các bậc của các đỉnh là 2 + 2 + 3 = 7 là một số lẻ.
Thực hành 2
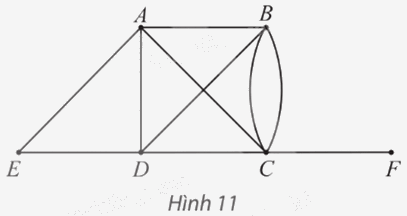
Cho đồ thị như Hình 11.

a) Hãy chỉ ra bậc của tất cả các đỉnh và tìm tổng của chúng.
b) Tìm tất cả các đỉnh kề với đỉnh B. Số đỉnh này có bằng bậc của đỉnh B không?
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là d(A)
Lời giải chi tiết:
a) Số cạnh của đồ thị có A là đầu mút là: 4.Suy ra bậc của đỉnh A là: d(A) = 4.
Tương tự như vậy, ta có: d(B) = 4; d(C) = 5; d(D) = 4; d(E) = 2; d(F) = 1.
Tổng các bậc của các đỉnh của đồ thị là: 4 + 4 + 5 + 4 + 2 + 1 = 20.
b) Tất cả các đỉnh kề với đỉnh B là: A, C, D.Suy ra có 3 đỉnh kề với đỉnh B.
Mà bậc của đỉnh B là: d(B) = 4.
Vì 3 ≠ 4 nên 3 ≠ d(B).
Vậy số đỉnh kề với đỉnh B không bằng bậc của đỉnh B.
Khám phá 2
Đồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng). Biết rằng mỗi con đường ra, vào làng đều phải đi qua một cổng chào; hai con đường khác nhau thì ra, vào làng qua hai cổng chào khác nhau. Ngoài ra, các ngôi làng không còn cổng chào nào khác.
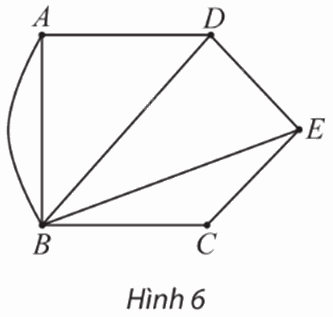
a) Ngôi làng nào có ít cổng chào nhất? Ngôi làng nào có nhiều cổng chào nhất?
b) Năm ngôi làng có tất cả bao nhiêu cổng chào?
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
a) Do ta có 3 con đường để ra, vào ngôi làng A nên ngôi làng A có 3 cổng chào.
Tương tự như vậy, ta có:
⦁ Ngôi làng B có 5 cổng chào;
⦁ Ngôi làng C có 2 cổng chào;
⦁ Ngôi làng D có 3 cổng chào;
⦁ Ngôi làng E có 3 cổng chào.
Vậy ngôi làng có ít cổng chào nhất là ngôi làng C (với 2 cổng chào); ngôi làng có nhiều cổng chào nhất là ngôi làng B (với 5 cổng chào).
b) Quan sát Hình 6, đồ thị có tất cả 8 cạnh (mỗi cạnh biểu diễn 1 con đường giữa hai ngôi làng) nên năm ngôi làng có tất cả 8 cổng chào.
- Khám phá 2
- Thực hành 2
- Vận dụng 2
Đồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng). Biết rằng mỗi con đường ra, vào làng đều phải đi qua một cổng chào; hai con đường khác nhau thì ra, vào làng qua hai cổng chào khác nhau. Ngoài ra, các ngôi làng không còn cổng chào nào khác.
a) Ngôi làng nào có ít cổng chào nhất? Ngôi làng nào có nhiều cổng chào nhất?
b) Năm ngôi làng có tất cả bao nhiêu cổng chào?
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
a) Do ta có 3 con đường để ra, vào ngôi làng A nên ngôi làng A có 3 cổng chào.
Tương tự như vậy, ta có:
⦁ Ngôi làng B có 5 cổng chào;
⦁ Ngôi làng C có 2 cổng chào;
⦁ Ngôi làng D có 3 cổng chào;
⦁ Ngôi làng E có 3 cổng chào.
Vậy ngôi làng có ít cổng chào nhất là ngôi làng C (với 2 cổng chào); ngôi làng có nhiều cổng chào nhất là ngôi làng B (với 5 cổng chào).
b) Quan sát Hình 6, đồ thị có tất cả 8 cạnh (mỗi cạnh biểu diễn 1 con đường giữa hai ngôi làng) nên năm ngôi làng có tất cả 8 cổng chào.
Cho đồ thị như Hình 11.
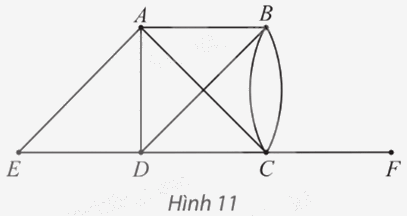
a) Hãy chỉ ra bậc của tất cả các đỉnh và tìm tổng của chúng.
b) Tìm tất cả các đỉnh kề với đỉnh B. Số đỉnh này có bằng bậc của đỉnh B không?
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là d(A)
Lời giải chi tiết:
a) Số cạnh của đồ thị có A là đầu mút là: 4.Suy ra bậc của đỉnh A là: d(A) = 4.
Tương tự như vậy, ta có: d(B) = 4; d(C) = 5; d(D) = 4; d(E) = 2; d(F) = 1.
Tổng các bậc của các đỉnh của đồ thị là: 4 + 4 + 5 + 4 + 2 + 1 = 20.
b) Tất cả các đỉnh kề với đỉnh B là: A, C, D.Suy ra có 3 đỉnh kề với đỉnh B.
Mà bậc của đỉnh B là: d(B) = 4.
Vì 3 ≠ 4 nên 3 ≠ d(B).
Vậy số đỉnh kề với đỉnh B không bằng bậc của đỉnh B.
Có hay không một đồ thị có ba đỉnh, trong đó hai đỉnh có bậc bằng 2 và một đỉnh có bậc bằng 3?
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Không có, vì tổng tất cả các bậc của các đỉnh là 2 + 2 + 3 = 7 là một số lẻ.
Giải bài 2 trang 46, 47, 48 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 46, 47, 48 của Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng và kiến thức đã học. Tusach.vn sẽ đồng hành cùng các em để giải quyết bài tập một cách hiệu quả nhất.
Nội dung bài 2 trang 46, 47, 48
Bài 2 trong chuyên đề này thường xoay quanh các chủ đề sau:
- Đại số: Các bài toán về hàm số, phương trình, bất phương trình, hệ phương trình.
- Hình học: Các bài toán về vectơ, đường thẳng, đường tròn, mặt cầu.
- Phân tích: Các bài toán về giới hạn, đạo hàm, tích phân.
Hướng dẫn giải chi tiết
Để giải bài 2 trang 46, 47, 48, các em cần:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và kết quả cần tìm.
- Áp dụng kiến thức: Sử dụng các công thức, định lý, quy tắc đã học để giải quyết bài toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả tìm được là chính xác và phù hợp với điều kiện của bài toán.
Giải bài 2.1 trang 46
(Nội dung giải bài 2.1 trang 46 sẽ được trình bày chi tiết tại đây, bao gồm các bước giải, giải thích và kết luận.)
Giải bài 2.2 trang 47
(Nội dung giải bài 2.2 trang 47 sẽ được trình bày chi tiết tại đây, bao gồm các bước giải, giải thích và kết luận.)
Giải bài 2.3 trang 48
(Nội dung giải bài 2.3 trang 48 sẽ được trình bày chi tiết tại đây, bao gồm các bước giải, giải thích và kết luận.)
Lưu ý quan trọng
Trong quá trình giải bài tập, các em cần chú ý:
- Sử dụng máy tính bỏ túi khi cần thiết.
- Vẽ hình minh họa để dễ hình dung bài toán.
- Tham khảo các tài liệu tham khảo khác để mở rộng kiến thức.
Tusach.vn – Người bạn đồng hành đáng tin cậy
Tusach.vn luôn cập nhật lời giải các bài tập Toán 11 Chân trời sáng tạo một cách nhanh chóng và chính xác. Chúng tôi hy vọng rằng, với sự hỗ trợ của Tusach.vn, các em sẽ học tập tốt hơn và đạt được kết quả cao trong môn Toán.
Bảng tổng hợp các công thức liên quan
| Công thức | Mô tả |
|---|---|
| (Công thức 1) | (Mô tả công thức 1) |
| (Công thức 2) | (Mô tả công thức 2) |
Chúc các em học tập tốt!