Giải bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng Tusach.vn khám phá lời giải chi tiết bài tập này ngay nhé!
Cho tam giác ABC có góc B, góc C đều là góc nhọn.
Đề bài
Cho tam giác ABC có góc B, góc C đều là góc nhọn. Nêu cách vẽ hình chữ nhật DEFG có đỉnh D, đỉnh E thuộc cạnh BC, đỉnh F, đỉnh G thuộc cạnh AC, AB và có EF = 2DE.
Phương pháp giải - Xem chi tiết
Dựa vào phép vị tự để làm: Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết
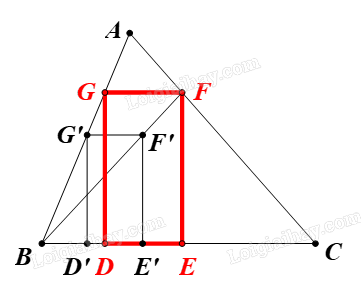
⦁ Phân tích:
Lấy điểm G’ bất kì trên AB.
Dựng hình chữ nhật D’E’F’G’ có \(\;E'F'{\rm{ }} = {\rm{ }}2D'E'\) và hai đỉnh D’, E’ thuộc BC.
Đường thẳng BF’ cắt AC tại F.
Do D’E’F’G’ là hình chữ nhật nên \(G'D'{\rm{ }} \bot {\rm{ }}D'E'\) hay \(G'D'{\rm{ }} \bot {\rm{ }}BC.\)
Mà GD ⊥ BC (do DEFG là hình chữ nhật).
Nên G’D’ // GD.
Chứng minh tương tự, ta được E’F’ // EF.
Vì D’E’F’G’ là hình chữ nhật nên G’F’ // D’E’ hay G’F’ // BC.
Mà GF // BC (do DEFG là hình chữ nhật).
Suy ra GF // G’F’.
Áp dụng định lí Thales, ta được \(\frac{{BG}}{{BG'}} = \frac{{BF}}{{BF'}}\)
Suy ra \(BF' = \frac{{BG'}}{{BG}}.BF\)
Mà \(\overrightarrow {BF'} ,\overrightarrow {BF} \) cùng hướng.
Do đó \(\overrightarrow {BF'} = \frac{{BG'}}{{BG}}.\overrightarrow {BF} \)
Vì vậy \({\rm{F'}} = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( F \right)\,\,(1)\)
Chứng minh tương tự, ta được \(D' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( D \right)\) và \(E' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( E \right)\,\,(2)\)
Lại có \(G' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( G \right)\,\,(3)\)
Từ (1), (2), (3), ta thu được \({V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\) biến hình chữ nhật D’E’F’G’ thành hình chữ nhật DEFG. Từ đó, ta suy ra cách dựng hình chữ nhật DEFG.
⦁ Cách dựng:
Lấy điểm G’ tùy ý trên AB.
Dựng hình chữ nhật D’E’F’G’ có E’F’ = 2D’E’, hai đỉnh D’, E’ nằm trên BC.
Đường thẳng BF’ cắt AC tại F.
Đường thẳng qua F song song với BC cắt AB tại G.
Gọi D, E lần lượt là hình chiếu của G, F lên BC.
Vậy ta đã dựng xong hình chữ nhật DEFG.
Giải bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, đạo hàm của hàm số hợp, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung chi tiết bài 18 trang 42
Bài 18 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số phức tạp, thường sử dụng quy tắc đạo hàm của hàm hợp, quy tắc tích, quy tắc thương.
- Dạng 2: Khảo sát hàm số: Xác định khoảng đơn điệu, cực trị, điểm uốn của hàm số bằng cách sử dụng đạo hàm.
- Dạng 3: Ứng dụng đạo hàm để giải quyết các bài toán thực tế: Ví dụ như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trong một khoảng cho trước.
Lời giải chi tiết bài 18 trang 42 (Ví dụ)
Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể. Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2.
- Bước 1: Tính đạo hàm f'(x): Sử dụng quy tắc đạo hàm của lũy thừa, ta có f'(x) = 3x2 - 6x.
- Bước 2: Tìm cực trị: Cho f'(x) = 0, ta có 3x2 - 6x = 0 => x = 0 hoặc x = 2.
- Bước 3: Xác định khoảng đơn điệu: Xét dấu f'(x) trên các khoảng (-∞, 0), (0, 2), (2, +∞) để xác định khoảng hàm số đồng biến và nghịch biến.
- Bước 4: Kết luận: Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán để kiểm tra kết quả.
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn là website cung cấp tài liệu học tập và giải bài tập Toán 11 uy tín, chất lượng. Chúng tôi luôn cập nhật những lời giải chi tiết, dễ hiểu, giúp các em học sinh học tập hiệu quả và đạt kết quả tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chủ đề | Nội dung |
|---|---|
| Đạo hàm | Khái niệm, quy tắc tính đạo hàm |
| Ứng dụng đạo hàm | Khảo sát hàm số, tìm cực trị |
| Chuyên đề học tập Toán 11 | Giải bài tập, luyện tập |
| Tusach.vn - Nguồn tài liệu học tập Toán 11 đáng tin cậy | |