Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Chuyên đề 1. Phép biến hình phẳng
Bài 7. Phép đồng dạng

Giải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Giải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Tusach.vn xin giới thiệu lời giải chi tiết bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 11 Chân trời sáng tạo, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.

Cho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC

Đề bài

Cho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hình thang JLKI và hình thang IHDC đồng dạng với nhau.

Phương pháp giải - Xem chi tiếtGiải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo 1

Dựa vào các phép biến hình đã học để làm

Lời giải chi tiết

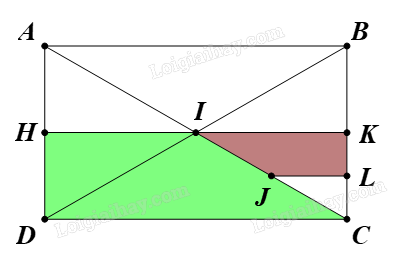
Giải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo 2

Ta có J là trung điểm IC (giả thiết).

Suy ra \(\overrightarrow {CI} = 2\overrightarrow {CJ} \)

Do đó \({V_{\left( {C,{\rm{ }}2} \right)}}\left( J \right){\rm{ }} = {\rm{ }}I.\)

Chứng minh tương tự, ta được \({V_{\left( {C,{\rm{ }}2} \right)}}\left( L \right){\rm{ }} = {\rm{ }}K,{\rm{ }}{V_{\left( {C,{\rm{ }}2} \right)}}\left( K \right){\rm{ }} = {\rm{ }}B,{\rm{ }}{V_{\left( {C,{\rm{ }}2} \right)}}\left( I \right){\rm{ }} = {\rm{ }}A.\)

Vì vậy \({V_{\left( {C,{\rm{ }}2} \right)}}\;\) biến hình thang JLKI thành hình thang IKBA.

Hình chữ nhật ABCD có I là giao điểm của hai đường chéo, suy ra I là trung điểm BD.

Do đó \({Đ_I}\left( B \right){\rm{ }} = {\rm{ }}D.\)

Chứng minh tương tự, ta được \({Đ_I}\left( A \right){\rm{ }} = {\rm{ }}C,{\rm{ }}{Đ_I}\left( K \right){\rm{ }} = {\rm{ }}H.\)

Lại có \({Đ_I}\left( I \right){\rm{ }} = {\rm{ }}I.\)

Do đó ĐI biến hình thang IKBA thành hình thang IHDC.

Vì vậy phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm C, tỉ số 2 và phép đối xứng tâm I biến hình thang JLKI thành hình thang IHDC.

Vậy hình thang JLKI và hình thang IHDC đồng dạng với nhau.

Giải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp

Bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc ôn tập và củng cố kiến thức về dãy số, cấp số cộng, cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức, tính chất của dãy số để giải quyết các bài toán thực tế.

Nội dung chi tiết bài 1 trang 40

Bài 1 thường bao gồm các dạng bài tập sau:

  • Dạng 1: Xác định số hạng tổng quát của dãy số. Yêu cầu học sinh tìm công thức biểu diễn số hạng thứ n của dãy số dựa trên các thông tin đã cho.
  • Dạng 2: Tính tổng của n số hạng đầu tiên của dãy số. Sử dụng công thức tính tổng của cấp số cộng hoặc cấp số nhân để tìm tổng.
  • Dạng 3: Ứng dụng dãy số vào các bài toán thực tế. Ví dụ như tính số tiền lãi sau một số kỳ hạn, tính số lượng sản phẩm sản xuất được sau một số năm.

Lời giải chi tiết bài 1 trang 40 (Ví dụ)

Đề bài: Cho dãy số (un) với u1 = 2 và un+1 = 2un + 1. Tính u5.

Lời giải:

  1. u2 = 2u1 + 1 = 2(2) + 1 = 5
  2. u3 = 2u2 + 1 = 2(5) + 1 = 11
  3. u4 = 2u3 + 1 = 2(11) + 1 = 23
  4. u5 = 2u4 + 1 = 2(23) + 1 = 47

Vậy u5 = 47.

Mẹo giải bài tập dãy số hiệu quả

Để giải các bài tập về dãy số một cách hiệu quả, bạn nên:

  • Nắm vững các công thức, tính chất của dãy số, cấp số cộng, cấp số nhân.
  • Phân tích kỹ đề bài để xác định đúng dạng bài tập và phương pháp giải phù hợp.
  • Thực hành giải nhiều bài tập khác nhau để rèn luyện kỹ năng và kinh nghiệm.
  • Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

Tusach.vn là website cung cấp tài liệu học tập, giải bài tập trực tuyến uy tín và chất lượng. Chúng tôi luôn cố gắng mang đến cho học sinh những trải nghiệm học tập tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Bảng tổng hợp công thức dãy số (Tham khảo)

Công thứcMô tả
un = u1 + (n-1)dSố hạng tổng quát của cấp số cộng
Sn = n/2 (u1 + un)Tổng của n số hạng đầu tiên của cấp số cộng
un = u1qn-1Số hạng tổng quát của cấp số nhân
Sn = u1(1-qn)/(1-q)Tổng của n số hạng đầu tiên của cấp số nhân (q ≠ 1)

Hy vọng bài giải này sẽ giúp bạn hiểu rõ hơn về bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN