Giải mục 2 trang 39, 40 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 39, 40 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 39, 40 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài giải này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, giúp học sinh hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải quyết vấn đề.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của các em.
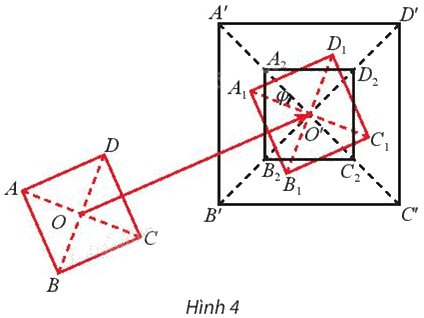
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
Vận dụng 2
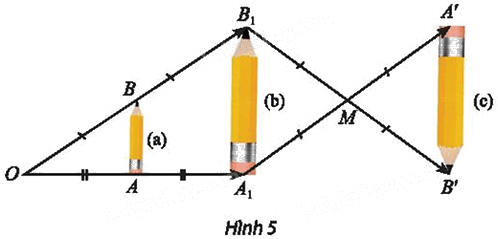
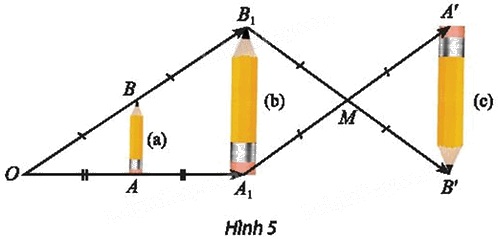
Tìm các cặp hình đồng dạng với nhau có trong Hình 5.

Phương pháp giải:
Quan sát hình 5 để tìm các cặp hình đồng dạng
Lời giải chi tiết:
⦁ Xét cặp hình (a) và (b):
Ta có \(O{A_1}\; = {\rm{ }}2OA\) và \(\overrightarrow {O{A_1}} \;,\,\overrightarrow {OA} \) cùng phương.
Suy ra \(\overrightarrow {O{A_1}} = 2\,\overrightarrow {OA} \)
Do đó \({V_{\left( {O,{\rm{ }}2} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Chứng minh tương tự, ta được \({V_{\left( {O,{\rm{ }}2} \right)}}\left( B \right){\rm{ }} = {\rm{ }}{B_1}.\)
Vì vậy \({V_{\left( {O,{\rm{ }}2} \right)}}\left( {AB} \right){\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Khi đó \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) biến hình (a) thành hình (b).
Vì vậy phép đồng dạng tỉ số 2 biến hình (a) thành hình (b).
Do đó hình (a) và hình (b) đồng dạng với nhau.
⦁ Ta xét hình (b) và hình (c):
Ta có M là trung điểm B1B’.
Suy ra \(B'{\rm{ }} = {\rm{ }}{Đ_M}({B_1}).\)
Chứng minh tương tự, ta được \(A'{\rm{ }} = {\rm{ }}{Đ_M}({A_1}).\)
Do đó
Khi đó \({Đ_M}\) biến hình (b) thành hình (c).
Vì vậy phép đồng dạng tỉ số 1 biến hình (b) thành hình (c).
Do đó hình (b) và hình (c) đồng dạng với nhau.
⦁ Ta xét hình (a) và hình (c):
Ta có phép đồng dạng có được bằng cách thực hiện liên tiếp \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) và \({Đ_M}\) biến hình (a) thành hình (c).
Do đó hình (a) và hình (c) đồng dạng với nhau.
Vậy các cặp hình đồng dạng với nhau có trong Hình 5 là: cặp hình (a) và (b); cặp hình (b) và (c); cặp hình (c) và (a).
Thực hành 2
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
a) Gọi \({A_1}{B_1}{C_1}{Đ_1}\) là ảnh của hình vuông ABCD qua phép tịnh tiến theo vectơ . Gọi φ là góc lượng giác (O’A1, O’A’). Tìm ảnh \({A_2}{B_2}{C_2}{Đ_2}\) của hình vuông A1B1C1D1 qua phép quay \({Q_{\left( {O',{\rm{ }}\varphi } \right)}}.\)
b) Cho biết \(\overrightarrow {OA'} = k\overrightarrow {O{A_2}} \). Tìm ảnh của hình vuông \({A_2}{B_2}{C_2}{Đ_2}\) qua phép vị tự \({V_{\left( {O',{\rm{ }}k} \right)}}.\)
c) Từ kết quả của câu a) và b), hãy cho biết ta có thể kết luận là hai hình vuông tùy ý luôn đồng dạng với nhau được không. Giải thích.
Phương pháp giải:
Để tìm ảnh của một hình qua một phép biến hình ta tìm ảnh của các điểm thuộc hình đó qua phép biến hình. Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
a) Do phép quay là phép dời hình nên ảnh A2B2C2D2 của hình vuông A1B1C1D1 cũng là hình vuông có kích thước bằng hình vuông A1B1C1D1.
Theo đề, ta có A1B1C1D1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo \(\overrightarrow {{\rm{OO}}'} \).
Mà O là tâm của hình vuông ABCD.
Nên ta có O’ là tâm của hình vuông A1B1C1D1.
Mà A2B2C2D2 là ảnh của hình vuông A1B1C1D1 qua \({Q_{(O',\;\varphi )}}\;\) (giả thiết).
Suy ra O’ cũng là tâm của hình vuông A2B2C2D2.
Do đó O’A2 = O’B2 = O’C2 = O’D2.
Để tìm ảnh A2B2C2D2 của hình vuông A1B1C1D1 qua ta tìm vị trí các điểm A2, B2, C2, D2 theo thứ tự là ảnh của các điểm A1, B1, C1, D1 qua \({Q_{(O',\;\varphi )}}.\)
Ta có \({A_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({A_1}).\)
Suy ra \(O'{A_2}\; = {\rm{ }}O'{A_1}\;,{\rm{ }}(O'{A_1},{\rm{ }}O'{A_2}){\rm{ }} = {\rm{ }}\varphi .\)
Mà \(\varphi {\rm{ }} = {\rm{ }}(O'{A_1},{\rm{ }}O'A')\) (giả thiết).
Do đó A2 nằm trên đường thẳng O’A’.
Vì vậy A2 là một điểm nằm trên đường thẳng O’A’ thỏa mãn O’A2 = O’A1.
Ta có \({B_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({B_1}).\)
Suy ra \(O'{B_2}\; = {\rm{ }}O'{B_1},(O'{B_1},{\rm{ }}O'{B_2}){\rm{ }} = {\rm{ }}\varphi .\)
Ta có O’ là tâm của hình vuông A2B2C2D2 và hình vuông A’B’C’D’.
Khi đó \(\widehat {{A_1}O'B} = {90^o} - \widehat {{A_2}O'{A_1}}\) và \(\widehat {{A_1}O'B'} = {90^o} - \widehat {A'O'{A_1}}\)
Suy ra \(\widehat {{A_1}O'{B_2}} = \widehat {{A_1}O'B'}\)
Do đó B2 nằm trên đường thẳng O’B’.
Vì vậy B2 là một điểm nằm trên đường thẳng O’B’ thỏa mãn \(O'{B_2}\; = {\rm{ }}O'{B_1}.\)
Chứng minh tương tự, ta được:
⦁ C2 nằm trên đường thẳng O’C’ thỏa mãn O’C2 = O’C1;
⦁ D2 nằm trên đường thẳng O’D’ thỏa mãn O’D2 = O’D1.
Vậy ảnh của hình vuông A1B1C1D1 qua Q(O’, φ) là hình vuông A2B2C2D2 thỏa mãn A2, B2, C2, D2 lần lượt nằm trên O’A’, O’B’, O’C’, O’D’ và O’B2 = O’C2 = O’D2 = O’A2 = O’A1.
b) Để tìm ảnh của hình vuông A2B2C2D2 qua V(O’, k), ta tìm ảnh của các điểm A2, B2, C2, D2 qua V(O’, k).
Theo đề, ta có \(\overrightarrow {O'A'} = k\overrightarrow {O'{A_2}} \) .
Suy ra \({V_{\left( {O',{\rm{ }}k} \right)}}({A_2}){\rm{ }} = {\rm{ }}A',{\rm{ }}O'A'{\rm{ }} = {\rm{ }}\left| k \right|.O'{A_2}.\)
Ta có O’A2 = O’B2 (chứng minh trên) và O’A’ = O’B’ (O’ là tâm của hình vuông A’B’C’D’).
Suy ra \(\frac{{O'{B_2}}}{{O'B'}} = \frac{{O'{A_2}}}{{O'A'}} = \frac{1}{{\left| k \right|}}\)
Do đó O’B’ = |k|.O’B2.
Mà \(\overrightarrow {O'B'} ,\overrightarrow {O'{B_2}} \) cùng phương (B2 là một điểm nằm trên đường thẳng O’B’).
Suy ra \(\overrightarrow {O'B'} = k.\overrightarrow {O'{B_2}} \)
Do đó \({V_{\left( {O',{\rm{ }}k} \right)}}({B_2}){\rm{ }} = {\rm{ }}B'.\)
Chứng minh tương tự, ta được \({V_{\left( {O',{\rm{ }}k} \right)}}({C_2}){\rm{ }} = {\rm{ }}C',{\rm{ }}{V_{\left( {O',{\rm{ }}k} \right)}}({Đ_2}){\rm{ }} = {\rm{ }}D'.\)
Vậy ảnh của hình vuông A2B2C2D2 qua \({V_{\left( {O',{\rm{ }}k} \right)}}\;\) là hình vuông A’B’C’D’.
c) Từ kết quả của câu a) và b), ta thấy phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O’, góc quay φ = (O’A1, O’A’) và phép vị tự tâm O, tỉ số k biến hình vuông ABCD thành hình vuông A’B’C’D’.
Do đó hai hình vuông ABCD và A’B’C’D’ đồng dạng với nhau.
Vậy hai hình vuông tùy ý luôn đồng dạng với nhau.
- Thực hành 2
- Vận dụng 2
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
a) Gọi \({A_1}{B_1}{C_1}{Đ_1}\) là ảnh của hình vuông ABCD qua phép tịnh tiến theo vectơ . Gọi φ là góc lượng giác (O’A1, O’A’). Tìm ảnh \({A_2}{B_2}{C_2}{Đ_2}\) của hình vuông A1B1C1D1 qua phép quay \({Q_{\left( {O',{\rm{ }}\varphi } \right)}}.\)
b) Cho biết \(\overrightarrow {OA'} = k\overrightarrow {O{A_2}} \). Tìm ảnh của hình vuông \({A_2}{B_2}{C_2}{Đ_2}\) qua phép vị tự \({V_{\left( {O',{\rm{ }}k} \right)}}.\)
c) Từ kết quả của câu a) và b), hãy cho biết ta có thể kết luận là hai hình vuông tùy ý luôn đồng dạng với nhau được không. Giải thích.
Phương pháp giải:
Để tìm ảnh của một hình qua một phép biến hình ta tìm ảnh của các điểm thuộc hình đó qua phép biến hình. Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
a) Do phép quay là phép dời hình nên ảnh A2B2C2D2 của hình vuông A1B1C1D1 cũng là hình vuông có kích thước bằng hình vuông A1B1C1D1.
Theo đề, ta có A1B1C1D1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo \(\overrightarrow {{\rm{OO}}'} \).
Mà O là tâm của hình vuông ABCD.
Nên ta có O’ là tâm của hình vuông A1B1C1D1.
Mà A2B2C2D2 là ảnh của hình vuông A1B1C1D1 qua \({Q_{(O',\;\varphi )}}\;\) (giả thiết).
Suy ra O’ cũng là tâm của hình vuông A2B2C2D2.
Do đó O’A2 = O’B2 = O’C2 = O’D2.
Để tìm ảnh A2B2C2D2 của hình vuông A1B1C1D1 qua ta tìm vị trí các điểm A2, B2, C2, D2 theo thứ tự là ảnh của các điểm A1, B1, C1, D1 qua \({Q_{(O',\;\varphi )}}.\)
Ta có \({A_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({A_1}).\)
Suy ra \(O'{A_2}\; = {\rm{ }}O'{A_1}\;,{\rm{ }}(O'{A_1},{\rm{ }}O'{A_2}){\rm{ }} = {\rm{ }}\varphi .\)
Mà \(\varphi {\rm{ }} = {\rm{ }}(O'{A_1},{\rm{ }}O'A')\) (giả thiết).
Do đó A2 nằm trên đường thẳng O’A’.
Vì vậy A2 là một điểm nằm trên đường thẳng O’A’ thỏa mãn O’A2 = O’A1.
Ta có \({B_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({B_1}).\)
Suy ra \(O'{B_2}\; = {\rm{ }}O'{B_1},(O'{B_1},{\rm{ }}O'{B_2}){\rm{ }} = {\rm{ }}\varphi .\)
Ta có O’ là tâm của hình vuông A2B2C2D2 và hình vuông A’B’C’D’.
Khi đó \(\widehat {{A_1}O'B} = {90^o} - \widehat {{A_2}O'{A_1}}\) và \(\widehat {{A_1}O'B'} = {90^o} - \widehat {A'O'{A_1}}\)
Suy ra \(\widehat {{A_1}O'{B_2}} = \widehat {{A_1}O'B'}\)
Do đó B2 nằm trên đường thẳng O’B’.
Vì vậy B2 là một điểm nằm trên đường thẳng O’B’ thỏa mãn \(O'{B_2}\; = {\rm{ }}O'{B_1}.\)
Chứng minh tương tự, ta được:
⦁ C2 nằm trên đường thẳng O’C’ thỏa mãn O’C2 = O’C1;
⦁ D2 nằm trên đường thẳng O’D’ thỏa mãn O’D2 = O’D1.
Vậy ảnh của hình vuông A1B1C1D1 qua Q(O’, φ) là hình vuông A2B2C2D2 thỏa mãn A2, B2, C2, D2 lần lượt nằm trên O’A’, O’B’, O’C’, O’D’ và O’B2 = O’C2 = O’D2 = O’A2 = O’A1.
b) Để tìm ảnh của hình vuông A2B2C2D2 qua V(O’, k), ta tìm ảnh của các điểm A2, B2, C2, D2 qua V(O’, k).
Theo đề, ta có \(\overrightarrow {O'A'} = k\overrightarrow {O'{A_2}} \) .
Suy ra \({V_{\left( {O',{\rm{ }}k} \right)}}({A_2}){\rm{ }} = {\rm{ }}A',{\rm{ }}O'A'{\rm{ }} = {\rm{ }}\left| k \right|.O'{A_2}.\)
Ta có O’A2 = O’B2 (chứng minh trên) và O’A’ = O’B’ (O’ là tâm của hình vuông A’B’C’D’).
Suy ra \(\frac{{O'{B_2}}}{{O'B'}} = \frac{{O'{A_2}}}{{O'A'}} = \frac{1}{{\left| k \right|}}\)
Do đó O’B’ = |k|.O’B2.
Mà \(\overrightarrow {O'B'} ,\overrightarrow {O'{B_2}} \) cùng phương (B2 là một điểm nằm trên đường thẳng O’B’).
Suy ra \(\overrightarrow {O'B'} = k.\overrightarrow {O'{B_2}} \)
Do đó \({V_{\left( {O',{\rm{ }}k} \right)}}({B_2}){\rm{ }} = {\rm{ }}B'.\)
Chứng minh tương tự, ta được \({V_{\left( {O',{\rm{ }}k} \right)}}({C_2}){\rm{ }} = {\rm{ }}C',{\rm{ }}{V_{\left( {O',{\rm{ }}k} \right)}}({Đ_2}){\rm{ }} = {\rm{ }}D'.\)
Vậy ảnh của hình vuông A2B2C2D2 qua \({V_{\left( {O',{\rm{ }}k} \right)}}\;\) là hình vuông A’B’C’D’.
c) Từ kết quả của câu a) và b), ta thấy phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O’, góc quay φ = (O’A1, O’A’) và phép vị tự tâm O, tỉ số k biến hình vuông ABCD thành hình vuông A’B’C’D’.
Do đó hai hình vuông ABCD và A’B’C’D’ đồng dạng với nhau.
Vậy hai hình vuông tùy ý luôn đồng dạng với nhau.
Tìm các cặp hình đồng dạng với nhau có trong Hình 5.
Phương pháp giải:
Quan sát hình 5 để tìm các cặp hình đồng dạng
Lời giải chi tiết:
⦁ Xét cặp hình (a) và (b):
Ta có \(O{A_1}\; = {\rm{ }}2OA\) và \(\overrightarrow {O{A_1}} \;,\,\overrightarrow {OA} \) cùng phương.
Suy ra \(\overrightarrow {O{A_1}} = 2\,\overrightarrow {OA} \)
Do đó \({V_{\left( {O,{\rm{ }}2} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Chứng minh tương tự, ta được \({V_{\left( {O,{\rm{ }}2} \right)}}\left( B \right){\rm{ }} = {\rm{ }}{B_1}.\)
Vì vậy \({V_{\left( {O,{\rm{ }}2} \right)}}\left( {AB} \right){\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Khi đó \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) biến hình (a) thành hình (b).
Vì vậy phép đồng dạng tỉ số 2 biến hình (a) thành hình (b).
Do đó hình (a) và hình (b) đồng dạng với nhau.
⦁ Ta xét hình (b) và hình (c):
Ta có M là trung điểm B1B’.
Suy ra \(B'{\rm{ }} = {\rm{ }}{Đ_M}({B_1}).\)
Chứng minh tương tự, ta được \(A'{\rm{ }} = {\rm{ }}{Đ_M}({A_1}).\)
Do đó
Khi đó \({Đ_M}\) biến hình (b) thành hình (c).
Vì vậy phép đồng dạng tỉ số 1 biến hình (b) thành hình (c).
Do đó hình (b) và hình (c) đồng dạng với nhau.
⦁ Ta xét hình (a) và hình (c):
Ta có phép đồng dạng có được bằng cách thực hiện liên tiếp \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) và \({Đ_M}\) biến hình (a) thành hình (c).
Do đó hình (a) và hình (c) đồng dạng với nhau.
Vậy các cặp hình đồng dạng với nhau có trong Hình 5 là: cặp hình (a) và (b); cặp hình (b) và (c); cặp hình (c) và (a).
Giải mục 2 trang 39, 40 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 trang 39, 40 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức quan trọng. Tusach.vn sẽ cung cấp lời giải chi tiết từng bài tập, kèm theo các phân tích và giải thích rõ ràng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
Nội dung chính của Mục 2 trang 39, 40 (Ví dụ - cần điều chỉnh theo nội dung thực tế của sách)
Giả sử Mục 2 trang 39, 40 tập trung vào chủ đề “Đạo hàm của hàm số lượng giác”. Các bài tập thường yêu cầu học sinh:
- Tính đạo hàm của các hàm số lượng giác cơ bản (sin x, cos x, tan x, cot x).
- Áp dụng các quy tắc đạo hàm (quy tắc tổng, hiệu, tích, thương, hàm hợp) để tính đạo hàm của các hàm số phức tạp hơn.
- Giải các bài toán liên quan đến ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số lượng giác.
Hướng dẫn giải chi tiết từng bài tập
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong Mục 2 trang 39, 40:
Bài 1: Tính đạo hàm của hàm số y = sin(2x)
Lời giải:
Sử dụng quy tắc hàm hợp, ta có:
y' = cos(2x) * (2x)' = 2cos(2x)
Bài 2: Tìm đạo hàm của hàm số y = x2 + cos x
Lời giải:
Sử dụng quy tắc tổng, ta có:
y' = (x2)' + (cos x)' = 2x - sin x
Các lưu ý quan trọng khi giải bài tập
- Nắm vững các công thức đạo hàm cơ bản của các hàm số lượng giác.
- Áp dụng đúng các quy tắc đạo hàm để tránh sai sót.
- Kiểm tra lại kết quả sau khi tính toán.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp lời giải chính xác, dễ hiểu và đầy đủ cho tất cả các bài tập trong sách giáo khoa và các tài liệu tham khảo Toán 11. Chúng tôi hy vọng rằng với sự hỗ trợ của Tusach.vn, các em sẽ học tập hiệu quả hơn và đạt được kết quả tốt nhất trong môn Toán.
Bảng tổng hợp công thức đạo hàm lượng giác (Ví dụ)
| Hàm số y | Đạo hàm y' |
|---|---|
| sin x | cos x |
| cos x | -sin x |
| tan x | 1/cos2 x |
| cot x | -1/sin2 x |
Hãy truy cập Tusach.vn thường xuyên để cập nhật các lời giải mới nhất và nhận được sự hỗ trợ tốt nhất trong quá trình học tập!