Giải mục 2 trang 7, 8 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 7, 8 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 7 và 8 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu nhất.
Bài giải này sẽ giúp các em học sinh củng cố kiến thức, hiểu rõ bản chất của từng bài toán và tự tin hơn trong quá trình học tập.
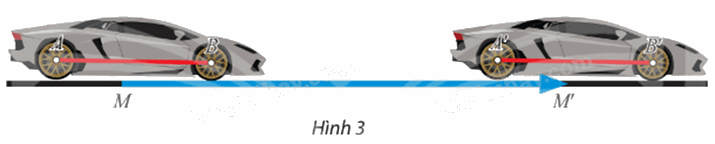
Khi một ô tô dời chỗ đậu từ vị trí M đến M’, khoảng cách giữa hai trục bánh xe có thay đổi không?
Khám phá 2
Khi một ô tô dời chỗ đậu từ vị trí M đến M’, khoảng cách giữa hai trục bánh xe có thay đổi không?
Phương pháp giải:
Quan sát hình 3 để trả lời
Lời giải chi tiết:
Khi một ô tô dời chỗ đậu từ vị trí M đến M’, khoảng cách giữa hai trục bánh xe không thay đổi.
Thực hành 2
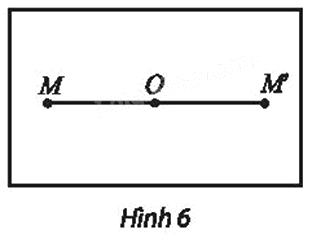
Cho điểm O trong mặt phẳng. Ta định nghĩa một phép biến hình h như sau: Với mỗi điểm M khác O chọn M’ = h(M) sao cho O là trung điểm của đoạn thẳng MM’ (Hình 6), còn với M trùng với O thì ta chọn O = h(M). Chứng minh h là một phép dời hình.
Phương pháp giải:
Phép dời hình là phép biến hình bảo toàn khoảng cách (không làm thay đổi khoảng cách) giữa 2 điểm bất kì.
Lời giải chi tiết:

⦁ Với hai điểm M, N khác O, ta đặt M’ = h(M) và N’ = h(N) với O là trung điểm của MM’ và O cũng là trung điểm của NN’.
Suy ra tứ giác MNM’N’ là hình bình hành.
Do đó MN = M’N’ (1)
⦁ Với M trùng O, ta có O = h(M).
Suy ra MO = 0 (2)
Từ (1), (2), ta thu được h là một phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Vậy h là một phép dời hình.
Vận dụng
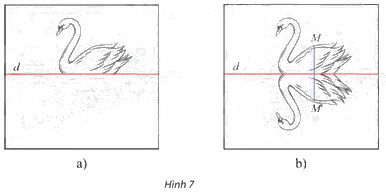
Một người đã vẽ xong bức tranh một con thiên nga đang bơi trên mặt hồ (đường thẳng d) (Hình 7a). Người đó muốn vẽ bóng của con thiên nga đó xuống mặt nước (như Hình 7b) bằng cách gấp tờ giấy theo đường thẳng d và đồ theo hình con thiên nga trên nửa tờ giấy còn lại. Chứng tỏ rằng đây là một phép dời hình.
Phương pháp giải:
Phép dời hình là phép biến hình bảo toàn khoảng cách (không làm thay đổi khoảng cách) giữa 2 điểm bất kì.
Lời giải chi tiết:
Ta đặt f là phép biến hình biến con thiên nga trong bức tranh thành bóng của con thiên nga đó qua đường thẳng d (mặt hồ).
Chọn M’ = f(M) hay M’ là điểm đối xứng của M qua d.
Suy ra d là đường trung trực của đoạn thẳng MM’.
Gọi H là giao điểm của MM’ và d.
Khi đó H là trung điểm của MM’ và MM’ ⊥ d tại H.
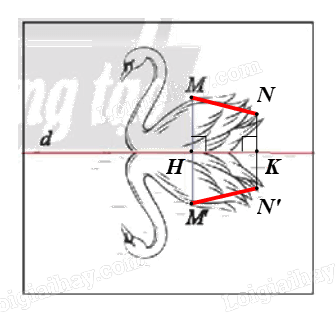
Trên hình 7b, chọn điểm N tùy ý trên con thiên nga đã vẽ trên mặt hồ (như hình vẽ).
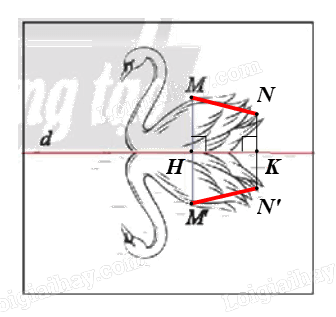
Chọn \(N' = f\left( N \right)\) hay N’ là điểm đối xứng của N qua d.
Suy ra d là đường trung trực của đoạn thẳng NN’.
Gọi K là giao điểm của NN’ và d.
Khi đó K là trung điểm của NN’ và NN’ ⊥ d tại K.
Ta có
\(\begin{array}{l}\overrightarrow {MN} + \overrightarrow {{\rm{M'N'}}} = \left( {\overrightarrow {MH} + \overrightarrow {HK} + \overrightarrow {KN} } \right) + \left( {\overrightarrow {{\rm{M'H}}} + \overrightarrow {HK} + \overrightarrow {KN'} } \right)\\ = \left( {\overrightarrow {MH} + \overrightarrow {{\rm{M'H}}} } \right) + \left( {\overrightarrow {KN} + \overrightarrow {KN'} } \right) + 2\overrightarrow {HK} \end{array}\)
\( = \vec 0 + \vec 0 + 2\overrightarrow {HK} \) (do H, K lần lượt là trung điểm của MM’, NN’)
\( = 2\overrightarrow {HK} \)
Lại có
\(\begin{array}{l}\overrightarrow {MN} - \overrightarrow {{\rm{M'N'}}} = \left( {\overrightarrow {HN} - \overrightarrow {HM} } \right) - \left( {\overrightarrow {HN'} - \overrightarrow {HM'} } \right)\\ = \overrightarrow {HN} - \overrightarrow {HM} - \overrightarrow {HN'} + \overrightarrow {HM'} = \left( {\overrightarrow {HN} - \overrightarrow {HN'} } \right) + \left( {\overrightarrow {HM'} - \overrightarrow {HM} } \right) = \overrightarrow {{\rm{N'N}}} + \overrightarrow {MM'} \end{array}\)
Ta có \({\overrightarrow {MN} ^2} - {\overrightarrow {{\rm{M'N'}}} ^2} = \left( {\overrightarrow {MN} + \overrightarrow {{\rm{M'N'}}} } \right)\left( {\overrightarrow {MN} - \overrightarrow {{\rm{M'N'}}} } \right) = 2\overrightarrow {HK} \left( {\overrightarrow {{\rm{N'N}}} + \overrightarrow {MM'} } \right)\) \( = 2\overrightarrow {HK} .\overrightarrow {{\rm{N'N}}} + 2\overrightarrow {HK} .\overrightarrow {MM'} = 2.0 + 2.0 = 0\) (do MM’ ⊥ d và NN’ ⊥ d).
Suy ra \({\overrightarrow {MN} ^2} = {\overrightarrow {{\rm{M'N'}}} ^2}\).
Do đó \(MN{\rm{ }} = {\rm{ }}M'N'.\)
Vì vậy phép biến hình f bảo toàn khoảng cách giữa hai điểm bất kì.
Vậy ta có điều phải chứng minh.
- Khám phá 2
- Thực hành 2
- Vận dụng
Khi một ô tô dời chỗ đậu từ vị trí M đến M’, khoảng cách giữa hai trục bánh xe có thay đổi không?
Phương pháp giải:
Quan sát hình 3 để trả lời
Lời giải chi tiết:
Khi một ô tô dời chỗ đậu từ vị trí M đến M’, khoảng cách giữa hai trục bánh xe không thay đổi.
Cho điểm O trong mặt phẳng. Ta định nghĩa một phép biến hình h như sau: Với mỗi điểm M khác O chọn M’ = h(M) sao cho O là trung điểm của đoạn thẳng MM’ (Hình 6), còn với M trùng với O thì ta chọn O = h(M). Chứng minh h là một phép dời hình.
Phương pháp giải:
Phép dời hình là phép biến hình bảo toàn khoảng cách (không làm thay đổi khoảng cách) giữa 2 điểm bất kì.
Lời giải chi tiết:

⦁ Với hai điểm M, N khác O, ta đặt M’ = h(M) và N’ = h(N) với O là trung điểm của MM’ và O cũng là trung điểm của NN’.
Suy ra tứ giác MNM’N’ là hình bình hành.
Do đó MN = M’N’ (1)
⦁ Với M trùng O, ta có O = h(M).
Suy ra MO = 0 (2)
Từ (1), (2), ta thu được h là một phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Vậy h là một phép dời hình.
Một người đã vẽ xong bức tranh một con thiên nga đang bơi trên mặt hồ (đường thẳng d) (Hình 7a). Người đó muốn vẽ bóng của con thiên nga đó xuống mặt nước (như Hình 7b) bằng cách gấp tờ giấy theo đường thẳng d và đồ theo hình con thiên nga trên nửa tờ giấy còn lại. Chứng tỏ rằng đây là một phép dời hình.
Phương pháp giải:
Phép dời hình là phép biến hình bảo toàn khoảng cách (không làm thay đổi khoảng cách) giữa 2 điểm bất kì.
Lời giải chi tiết:
Ta đặt f là phép biến hình biến con thiên nga trong bức tranh thành bóng của con thiên nga đó qua đường thẳng d (mặt hồ).
Chọn M’ = f(M) hay M’ là điểm đối xứng của M qua d.
Suy ra d là đường trung trực của đoạn thẳng MM’.
Gọi H là giao điểm của MM’ và d.
Khi đó H là trung điểm của MM’ và MM’ ⊥ d tại H.
Trên hình 7b, chọn điểm N tùy ý trên con thiên nga đã vẽ trên mặt hồ (như hình vẽ).
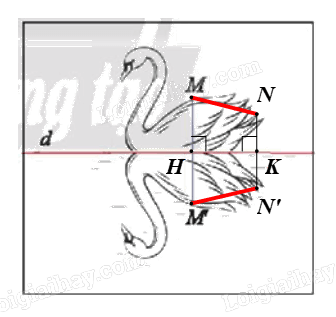
Chọn \(N' = f\left( N \right)\) hay N’ là điểm đối xứng của N qua d.
Suy ra d là đường trung trực của đoạn thẳng NN’.
Gọi K là giao điểm của NN’ và d.
Khi đó K là trung điểm của NN’ và NN’ ⊥ d tại K.
Ta có
\(\begin{array}{l}\overrightarrow {MN} + \overrightarrow {{\rm{M'N'}}} = \left( {\overrightarrow {MH} + \overrightarrow {HK} + \overrightarrow {KN} } \right) + \left( {\overrightarrow {{\rm{M'H}}} + \overrightarrow {HK} + \overrightarrow {KN'} } \right)\\ = \left( {\overrightarrow {MH} + \overrightarrow {{\rm{M'H}}} } \right) + \left( {\overrightarrow {KN} + \overrightarrow {KN'} } \right) + 2\overrightarrow {HK} \end{array}\)
\( = \vec 0 + \vec 0 + 2\overrightarrow {HK} \) (do H, K lần lượt là trung điểm của MM’, NN’)
\( = 2\overrightarrow {HK} \)
Lại có
\(\begin{array}{l}\overrightarrow {MN} - \overrightarrow {{\rm{M'N'}}} = \left( {\overrightarrow {HN} - \overrightarrow {HM} } \right) - \left( {\overrightarrow {HN'} - \overrightarrow {HM'} } \right)\\ = \overrightarrow {HN} - \overrightarrow {HM} - \overrightarrow {HN'} + \overrightarrow {HM'} = \left( {\overrightarrow {HN} - \overrightarrow {HN'} } \right) + \left( {\overrightarrow {HM'} - \overrightarrow {HM} } \right) = \overrightarrow {{\rm{N'N}}} + \overrightarrow {MM'} \end{array}\)
Ta có \({\overrightarrow {MN} ^2} - {\overrightarrow {{\rm{M'N'}}} ^2} = \left( {\overrightarrow {MN} + \overrightarrow {{\rm{M'N'}}} } \right)\left( {\overrightarrow {MN} - \overrightarrow {{\rm{M'N'}}} } \right) = 2\overrightarrow {HK} \left( {\overrightarrow {{\rm{N'N}}} + \overrightarrow {MM'} } \right)\) \( = 2\overrightarrow {HK} .\overrightarrow {{\rm{N'N}}} + 2\overrightarrow {HK} .\overrightarrow {MM'} = 2.0 + 2.0 = 0\) (do MM’ ⊥ d và NN’ ⊥ d).
Suy ra \({\overrightarrow {MN} ^2} = {\overrightarrow {{\rm{M'N'}}} ^2}\).
Do đó \(MN{\rm{ }} = {\rm{ }}M'N'.\)
Vì vậy phép biến hình f bảo toàn khoảng cách giữa hai điểm bất kì.
Vậy ta có điều phải chứng minh.
Giải mục 2 trang 7, 8 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng vào giải quyết các bài tập thực tế. Việc hiểu rõ bản chất của từng khái niệm và công thức là vô cùng quan trọng để đạt kết quả tốt trong các bài kiểm tra và kỳ thi.
Nội dung chính của Mục 2 (trang 7, 8)
Để giải quyết hiệu quả các bài tập trong mục này, trước tiên chúng ta cần xác định rõ nội dung chính mà Chuyên đề học tập Toán 11 - Chân trời sáng tạo muốn truyền tải. Thông thường, mục 2 sẽ đi sâu vào một trong các chủ đề sau:
- Hàm số lượng giác: Khái niệm, tính chất, đồ thị và ứng dụng của các hàm số lượng giác (sin, cos, tan, cot).
- Phương trình lượng giác: Các phương pháp giải phương trình lượng giác cơ bản và nâng cao.
- Đạo hàm: Khái niệm đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
- Giới hạn: Khái niệm giới hạn, các tính chất của giới hạn và ứng dụng của giới hạn trong việc tính tích phân.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong mục 2 trang 7, 8 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Lưu ý rằng, các bài tập có thể khác nhau tùy thuộc vào từng phiên bản sách.
Ví dụ 1: Giải phương trình lượng giác sin(x) = 1/2
Lời giải:
- Phương trình sin(x) = 1/2 có nghiệm là:
- x = arcsin(1/2) + k2π = π/6 + k2π
- x = π - arcsin(1/2) + k2π = 5π/6 + k2π
- Với k ∈ Z
Ví dụ 2: Tính đạo hàm của hàm số f(x) = x2 + 2x - 1
Lời giải:
f'(x) = 2x + 2
Mẹo học tập hiệu quả
Để học tốt môn Toán 11, đặc biệt là phần Chuyên đề học tập, bạn nên:
- Nắm vững lý thuyết: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các khái niệm, định lý và công thức quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo, bạn bè hoặc tìm kiếm sự trợ giúp trên các trang web học tập trực tuyến như tusach.vn.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị, các ứng dụng học tập trên điện thoại có thể giúp bạn học tập hiệu quả hơn.
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp những lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi luôn cập nhật nội dung mới nhất và lắng nghe phản hồi từ người dùng để cải thiện chất lượng dịch vụ.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và cùng chúng tôi chinh phục những thử thách trong môn Toán!
| Chủ đề | Mức độ khó | Lời khuyên |
|---|---|---|
| Hàm số lượng giác | Trung bình | Nắm vững đường tròn lượng giác |
| Phương trình lượng giác | Khó | Luyện tập nhiều dạng bài |
| Đạo hàm | Trung bình | Hiểu rõ các quy tắc tính đạo hàm |