Giải mục 1 trang 6, 7 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 6, 7 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 6, 7 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi hy vọng sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.
Bài giải được trình bày rõ ràng, logic, kèm theo các lưu ý quan trọng để các em có thể tự học hiệu quả.
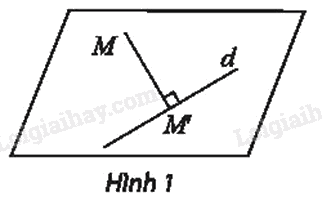
Trong mặt phẳng, cho đường thẳng d và điểm M. Gọi M’ là hình chiếu vuông góc của M trên đường thẳng d.
Thực hành 1
Trong mặt phẳng tọa độ Oxy, ứng mỗi điểm M(x; y) quy tắc f xác định điểm M’(–3x; 3y). Hãy cho biết f có phải là phép biến hình không. Nếu có, tìm ảnh của điểm A(–1; 2) qua f.
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
+ Theo đề, ta có f(M) = M’, với tọa độ M(x; y), M’(–3x; 3y).
Ta thấy f là một quy tắc sao cho: ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
+ Gọi A’ là ảnh của điểm A(–1; 2) qua phép biến hình f.
Ta có xA’ = –3xA = –3.(–1) = 3 và yA’ = 3yA = 3.2 = 6.
Vậy ảnh của điểm A(–1; 2) qua phép biến hình f là điểm A’(3; 6).
Khám phá 1
Trong mặt phẳng, cho đường thẳng d và điểm M. Gọi M’ là hình chiếu vuông góc của M trên đường thẳng d.
Vẽ ba điểm A, B, C tùy ý và tìm hình chiếu vuông góc A’, B’, C’ của chúng trên d.
Phương pháp giải:
Để tìm hình chiếu của một điểm A lên một đường thẳng d. Từ điểm A hạ đường thẳng AH vuông góc với d tại H. Khi đó, H là hình chiếu vuông góc của A lên d.
Lời giải chi tiết:
Giả sử chọn ba điểm A, B, C như hình vẽ dưới đây. Khi đó hình chiếu vuông góc A’, B’, C’ của chúng trên d được biểu diễn như hình vẽ dưới đây:

- Khám phá 1
- Thực hành 1
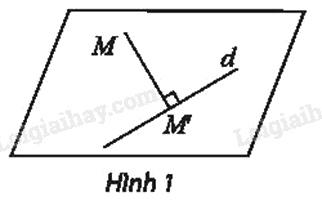
Trong mặt phẳng, cho đường thẳng d và điểm M. Gọi M’ là hình chiếu vuông góc của M trên đường thẳng d.
Vẽ ba điểm A, B, C tùy ý và tìm hình chiếu vuông góc A’, B’, C’ của chúng trên d.
Phương pháp giải:
Để tìm hình chiếu của một điểm A lên một đường thẳng d. Từ điểm A hạ đường thẳng AH vuông góc với d tại H. Khi đó, H là hình chiếu vuông góc của A lên d.
Lời giải chi tiết:
Giả sử chọn ba điểm A, B, C như hình vẽ dưới đây. Khi đó hình chiếu vuông góc A’, B’, C’ của chúng trên d được biểu diễn như hình vẽ dưới đây:

Trong mặt phẳng tọa độ Oxy, ứng mỗi điểm M(x; y) quy tắc f xác định điểm M’(–3x; 3y). Hãy cho biết f có phải là phép biến hình không. Nếu có, tìm ảnh của điểm A(–1; 2) qua f.
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
+ Theo đề, ta có f(M) = M’, với tọa độ M(x; y), M’(–3x; 3y).
Ta thấy f là một quy tắc sao cho: ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
+ Gọi A’ là ảnh của điểm A(–1; 2) qua phép biến hình f.
Ta có xA’ = –3xA = –3.(–1) = 3 và yA’ = 3yA = 3.2 = 6.
Vậy ảnh của điểm A(–1; 2) qua phép biến hình f là điểm A’(3; 6).
Giải mục 1 trang 6, 7 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về hàm số bậc hai. Đây là một phần kiến thức nền tảng quan trọng, không chỉ cho chương trình Toán 11 mà còn là bước đệm cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 1 trang 6, 7, đồng thời phân tích các phương pháp giải và những điểm cần lưu ý.
Nội dung chính của Mục 1
- Ôn tập về hàm số bậc hai: Định nghĩa, dạng tổng quát, đồ thị.
- Các tính chất của hàm số bậc hai: Sự biến thiên, giá trị lớn nhất, giá trị nhỏ nhất.
- Ứng dụng của hàm số bậc hai trong giải quyết các bài toán thực tế.
Giải chi tiết các bài tập trang 6
Chúng ta sẽ bắt đầu với việc giải chi tiết các bài tập trang 6. Các bài tập này thường tập trung vào việc xác định các hệ số của hàm số bậc hai, vẽ đồ thị và tìm các điểm đặc biệt của đồ thị (đỉnh, trục đối xứng, giao điểm với các trục tọa độ).
Ví dụ: Bài 1. Xác định hệ số a của hàm số y = ax2 + bx + c, biết rằng đồ thị của hàm số đi qua các điểm A(0; 1), B(1; 2) và C(-1; 0).
Lời giải:
- Thay tọa độ điểm A(0; 1) vào phương trình hàm số, ta được: 1 = a(0)2 + b(0) + c => c = 1.
- Thay tọa độ điểm B(1; 2) vào phương trình hàm số, ta được: 2 = a(1)2 + b(1) + 1 => a + b = 1.
- Thay tọa độ điểm C(-1; 0) vào phương trình hàm số, ta được: 0 = a(-1)2 + b(-1) + 1 => a - b = -1.
- Giải hệ phương trình: a + b = 1 và a - b = -1, ta được: a = 0 và b = 1.
- Vậy, hàm số có dạng: y = x + 1.
Giải chi tiết các bài tập trang 7
Các bài tập trang 7 thường phức tạp hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết. Các bài tập này có thể liên quan đến việc tìm điều kiện để phương trình bậc hai có nghiệm, tìm nghiệm của phương trình bậc hai, hoặc giải các bài toán ứng dụng liên quan đến hàm số bậc hai.
Ví dụ: Bài 2. Tìm giá trị của m để phương trình x2 - 2(m+1)x + 2m + 3 = 0 có hai nghiệm phân biệt.
Lời giải:
Để phương trình có hai nghiệm phân biệt, điều kiện cần và đủ là delta > 0.
Delta = (-2(m+1))2 - 4(1)(2m+3) = 4(m2 + 2m + 1) - 8m - 12 = 4m2 + 8m + 4 - 8m - 12 = 4m2 - 8.
Điều kiện delta > 0 tương đương với 4m2 - 8 > 0 => m2 > 2 => m > √2 hoặc m < -√2.
Lời khuyên khi giải bài tập
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
- Vận dụng các kiến thức đã học một cách linh hoạt.
- Kiểm tra lại kết quả sau khi giải xong.
- Tham khảo các nguồn tài liệu khác nhau để hiểu rõ hơn về bài toán.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 6, 7 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!