Giải bài 5 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 5 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 5 trang 24 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúng tôi sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết các bài toán tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Trong Hình 12, tìm phép đối xứng biến hình mũi tên (A) thành hình mũi tên (B) và tìm phép đối xứng biến hình mũi tên (B) thành hình mũi tên (C).
Đề bài
Trong Hình 12, tìm phép đối xứng biến hình mũi tên (A) thành hình mũi tên (B) và tìm phép đối xứng biến hình mũi tên (B) thành hình mũi tên (C).
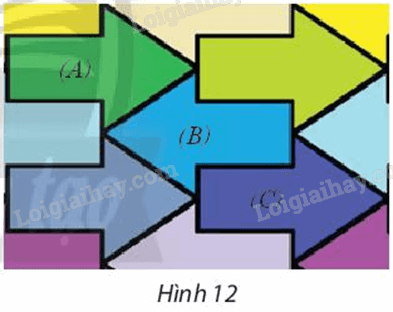
Phương pháp giải - Xem chi tiết
Quan sát hình 12 và dựa vào phép đối xứng tâm để làm.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết
⦁ Gọi P, Q là hai điểm nằm trên cạnh của mũi tên (A) như hình vẽ.
Lấy O là trung điểm của PQ.
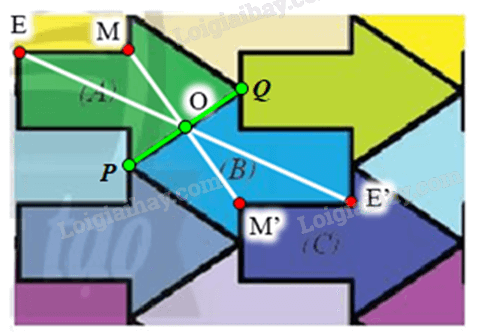
Gọi E là một điểm trên hình mũi tên (A).
Lấy điểm E’ là ảnh của E qua
Khi đó O là trung điểm của EE’, E’ một điểm trên hình mũi tên (B) có vị trí tương ứng với điểm E trên hình mũi tên (A).
Tương tự như vậy, với mỗi điểm M bất kì trên hình mũi tên (A), ta lấy điểm M’ là ảnh của M qua thì ta được tập hợp các điểm M’ tạo thành hình mũi tên (B).
Vậy phép đối xứng tâm O biến hình mũi tên (A) thành hình mũi tên (B), với O là trung điểm của PQ trên hình mũi tên (A) (như hình vẽ).
⦁ Gọi H, K là hai điểm nằm trên cạnh của mũi tên (B) như hình vẽ.
Lấy I là trung điểm của HK.
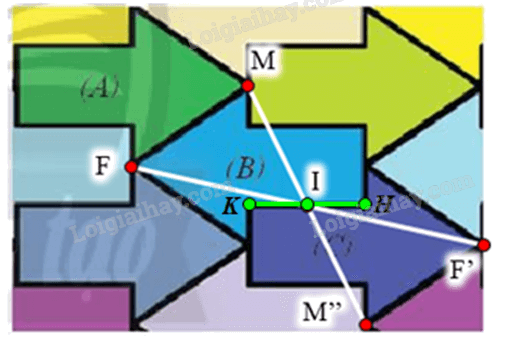
Chứng minh tương tự như trên, ta thu được phép đối xứng tâm I biến hình mũi tên (B) thành hình mũi tên (C), với I là trung điểm của HK trên hình mũi tên (B) (như hình vẽ).
Giải bài 5 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Hướng dẫn chi tiết
Bài 5 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung bài 5 trang 24
Bài 5 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, hàm hợp, hàm lượng giác,...
- Tìm đạo hàm cấp hai: Tính đạo hàm bậc hai của hàm số.
- Ứng dụng đạo hàm để xét tính đơn điệu của hàm số: Xác định khoảng đồng biến, nghịch biến của hàm số dựa vào dấu của đạo hàm.
- Tìm cực trị của hàm số: Xác định điểm cực đại, cực tiểu của hàm số.
- Giải các bài toán thực tế liên quan đến đạo hàm: Ví dụ như bài toán tìm vận tốc, gia tốc, tối ưu hóa,...
Lời giải chi tiết bài 5 trang 24
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài 5 trang 24, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi. Lưu ý rằng, trước khi bắt đầu giải bài tập, bạn cần nắm vững các kiến thức cơ bản về đạo hàm và các quy tắc tính đạo hàm.
Ví dụ minh họa (Giả định một phần của bài 5)
Câu a: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Lời giải:
f'(x) = 3x2 + 4x - 5
Các bước giải bài tập đạo hàm hiệu quả
- Xác định đúng công thức đạo hàm: Sử dụng các công thức đạo hàm cơ bản và quy tắc tính đạo hàm.
- Thực hiện các phép tính cẩn thận: Tránh sai sót trong quá trình tính toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả tính toán là chính xác.
- Vận dụng linh hoạt các kiến thức: Áp dụng các kiến thức về đạo hàm để giải quyết các bài toán khác nhau.
Mẹo học tốt môn Toán 11
Để học tốt môn Toán 11, bạn nên:
- Học lý thuyết kỹ càng: Nắm vững các định nghĩa, định lý, công thức.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
- Tìm kiếm sự giúp đỡ khi cần thiết: Hỏi thầy cô, bạn bè hoặc tham gia các diễn đàn học tập.
- Sử dụng các tài liệu học tập chất lượng: Sách giáo khoa, sách bài tập, tài liệu tham khảo,...
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn là website cung cấp tài liệu học tập Toán 11 uy tín và chất lượng. Chúng tôi cung cấp đầy đủ đáp án, lời giải chi tiết cho các bài tập trong sách giáo khoa, sách bài tập và các đề thi thử. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập!
| Công thức đạo hàm | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x2)' = 2x |
| (sin x)' = cos x | (sin x)' = cos x |