Giải bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
Cho phép tịnh tiến \({T_{\vec v}}\) và phép tịnh tiến \({T_{\vec v}}\).
Đề bài
Cho phép tịnh tiến \({T_{\vec v}}\) và phép tịnh tiến \({T_{\vec v}}\). Với điểm M bất kì, \({T_{\vec v}}\) biến M thành M’, \({T_{\vec v}}\) biến M’ thành M’’. Hỏi có phép tịnh tiến nào biến điểm M thành M’’ không?
Phương pháp giải - Xem chi tiết
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết
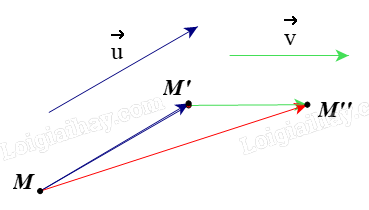
Theo đề, ta có \({T_{\vec u}}\left( M \right) = M'\), suy ra \(\overrightarrow {MM'} = \vec u\).
Ta lại có \({T_{\vec v}}\left( {M'} \right) = M''\), suy ra \(\overrightarrow {M'M''} = \vec v\).
Ta có \(\overrightarrow {MM''} = \overrightarrow {MM'} + \overrightarrow {M'M''} = \vec u + \vec v\)
Do đó \({T_{\vec u + \vec v}}\left( M \right) = M''\).
Vậy có phép tịnh tiến theo \(\vec u + \vec v\) biến điểm M thành điểm M’’.
Giải bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp giải
Bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số, vẽ đồ thị và tìm các điểm đặc biệt của đồ thị.
Nội dung chi tiết bài 1 trang 14
Bài 1 thường bao gồm các câu hỏi sau:
- Xác định hệ số a, b, c của hàm số bậc hai.
- Tìm tọa độ đỉnh của parabol.
- Tìm trục đối xứng của parabol.
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Vẽ đồ thị hàm số.
- Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Phương pháp giải bài 1 trang 14 hiệu quả
Để giải bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Công thức tính tọa độ đỉnh: xđỉnh = -b/2a, yđỉnh = -Δ/4a (với Δ = b2 - 4ac)
- Phương trình trục đối xứng: x = -b/2a
- Xác định khoảng đồng biến, nghịch biến: Dựa vào dấu của hệ số a.
- Cách vẽ đồ thị: Xác định các điểm đặc biệt (đỉnh, giao điểm với trục tung, giao điểm với trục hoành) và vẽ parabol.
Lời giải chi tiết bài 1 trang 14 (Ví dụ)
Đề bài: Cho hàm số y = x2 - 4x + 3. Hãy xác định tọa độ đỉnh, trục đối xứng và vẽ đồ thị hàm số.
Lời giải:
- Hệ số: a = 1, b = -4, c = 3
- Tọa độ đỉnh: xđỉnh = -(-4)/(2*1) = 2, yđỉnh = -( (-4)2 - 4*1*3 )/(4*1) = -(-4)/4 = 1. Vậy đỉnh là (2; 1).
- Trục đối xứng: x = 2
- Giao điểm với trục tung: (0; 3)
- Giao điểm với trục hoành: Giải phương trình x2 - 4x + 3 = 0, ta được x1 = 1, x2 = 3. Vậy giao điểm là (1; 0) và (3; 0).
Dựa vào các thông tin trên, bạn có thể vẽ được đồ thị hàm số.
Lưu ý khi giải bài tập
Khi giải bài tập về hàm số bậc hai, bạn cần chú ý:
- Kiểm tra kỹ các hệ số a, b, c.
- Sử dụng đúng công thức tính toán.
- Vẽ đồ thị chính xác.
- Phân tích kết quả và đưa ra kết luận hợp lý.
Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả
Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết và chính xác các bài tập Toán 11 Chân trời sáng tạo. Chúng tôi luôn cố gắng mang đến những tài liệu học tập tốt nhất để giúp bạn học tập hiệu quả và đạt kết quả cao.
Bảng tổng hợp các công thức quan trọng
| Công thức | Mô tả |
|---|---|
| xđỉnh = -b/2a | Hoành độ đỉnh của parabol |
| yđỉnh = -Δ/4a | Tung độ đỉnh của parabol |
| x = -b/2a | Phương trình trục đối xứng |