Giải bài 1 trang 44, 45, 46 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 1 trang 44, 45, 46 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 1 thuộc chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, phù hợp với chương trình học Toán 11 hiện hành.
Sử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây:
Khám phá 1
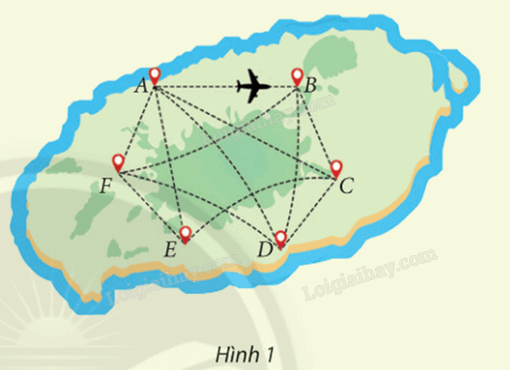
Sử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây:
a) Từ thành phố A, hãng X có bao nhiêu đường bay đến năm thành phố còn lại?
b) Giữa sáu thành phố trên, có tất cả bao nhiêu đường bay của hãng X?
c) Có thể giải đáp thắc mắc ở Hoạt động khởi động không?
Phương pháp giải:
Quan sát hình 1 để trả lời câu hỏi
Lời giải chi tiết:
a) Quan sát sơ đồ ở Hình 1, ta thấy:
⦁ Có 1 đường bay từ thành phố A đến thành phố B;
⦁ Có 1 đường bay từ thành phố A đến thành phố D;
⦁ Có 1 đường bay từ thành phố A đến thành phố E;
⦁ Có 1 đường bay từ thành phố A đến thành phố F.
Vậy từ thành phố A, hãng X có tất cả 4 đường bay đến năm thành phố còn lại.
b)Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố B đến thành phố A đã được tính vào đường bay từ thành phố A đến thành phố B.
Do đó từ thành phố B, hãng X có thêm:
⦁ 1 đường bay đến thành phố C;
⦁ 1 đường bay đến thành phố D;
⦁ 1 đường bay đến thành phố F.
Khi đó, từ thành phố B, hãng X có thêm 3 đường bay đến năm thành phố còn lại.
Tương tự như vậy, ta được:
– Từ thành phố C, hãng X có thêm 2 đường bay đến năm thành phố còn lại;
– Từ thành phố D, hãng X có thêm 1 đường bay đến năm thành phố còn lại;
– Từ thành phố E, hãng X có thêm 1 đường bay đến năm thành phố còn lại.
Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố F đến năm thành phố còn lại đã được tính vào các đường bay kể trên.
Vậy giữa sáu thành phố trên, có tất cả 4 + 3 + 2 + 1 + 1 = 11 đường bay của hãng X.
Chú ý: Ngoài cách trên, ta có thể đếm số đường cong và đường thẳng (thể hiện đường bay) trên Hình 1 (hoặc Bảng 1) để kết luận về số đường bay của hãng X.
c) Ta có thể giải đáp thắc mắc ở Hoạt động khởi động như sau:
Bước 1: Từ thành phố A bay đến thành phố B;
Bước 2: Từ thành phố B bay đến thành phố C;
Bước 3: Từ thành phố C bay đến thành phố D;
Bước 4: Từ thành phố D bay đến thành phố F;
Bước 5: Từ thành phố F bay đến thành phố E;
Bước 6: Từ thành phố E bay về thành phố A.
Vậy từ thành phố A, ta có thể thăm năm thành phố B, C, D, E và F bằng các chuyến bay của hãng X sao cho mỗi thành phố chỉ qua đúng một lần, rồi quay trở về A.
Chú ý: Ta có thể thay đổi thứ tự bay đến các thành phố chỉ cần hãng X có chuyến bay giữa hai thành phố liền kề.
Vận dụng 1
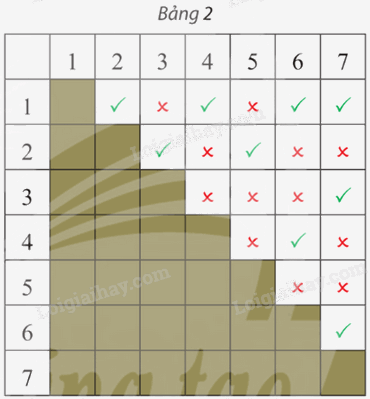
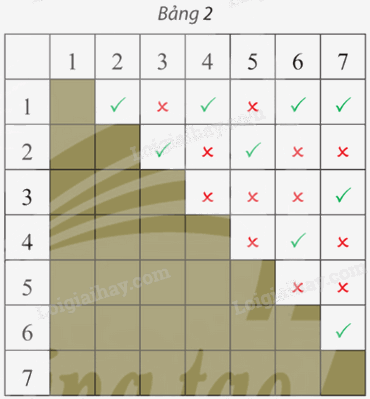
Một mạng cục bộ có bảy máy tính 1; 2; 3; 4; 5; 6 và 7. Bảng 2 cho biết giữa mỗi cặp máy tính có kết nối trực tiếp với nhau hay không (dấu ✔ là có kết nối, dấu ✘ là không kết nối). Hãy vẽ đồ thị biểu diễn sự kết nối giữa các máy tính của mạng này.
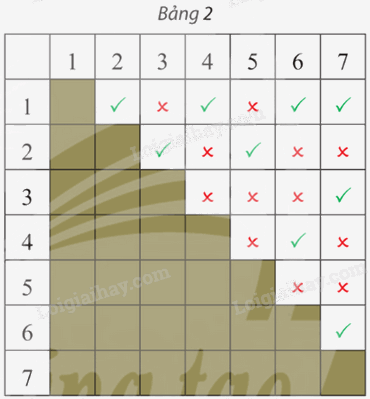
Phương pháp giải:
Dựa vào bảng 2 để vẽ đồ thị
Lời giải chi tiết:
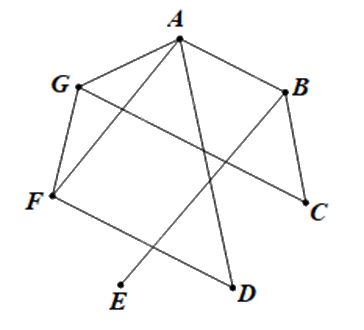
Ta vẽ đồ thị G có 7 đỉnh A, B, C, D, E, F, G lần lượt biểu diễn bảy máy tính 1; 2; 3; 4; 5; 6 và 7.
Hai đỉnh được nối bằng một cạnh nếu giữa hai máy tính có kết nối trực tiếp với nhau.
Ta có đồ thị G như sau:
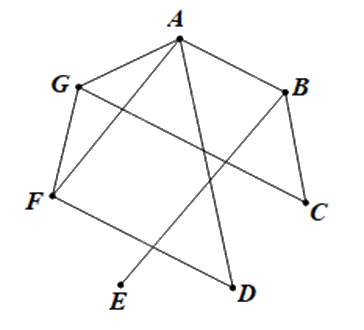
Thực hành 1
Cho đồ thị G như Hình 5.
a) Chỉ ra các đỉnh, các cạnh, số đỉnh, số cạnh của G.
b) Chỉ ra các đỉnh kề đỉnh D, các đỉnh kề đỉnh B.
c) Đồ thị G có đỉnh cô lập không?
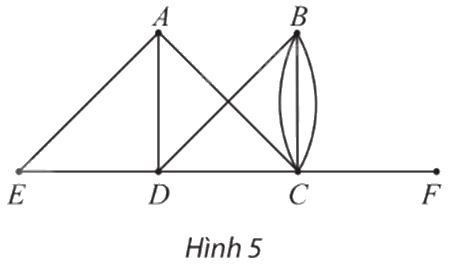
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
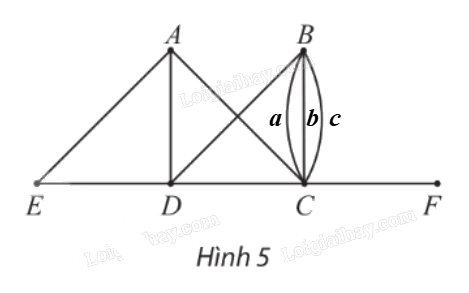
a) Các đỉnh của đồ thị G là: A, B, C, D, E và F. Đồ thị có 6 đỉnh.
Các cạnh của đồ thị G là: AC, AD, AE, a, b, c, BD, CD, CF, DE. Đồ thị có 10 cạnh.
b) Các đỉnh kề đỉnh D là: A, B, C, E.
Các đỉnh kề đỉnh B là: C, D.
c) Đồ thị G không có đỉnh cô lập.
- Khám phá 1
- Thực hành 1
- Vận dụng 1
Sử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây:
a) Từ thành phố A, hãng X có bao nhiêu đường bay đến năm thành phố còn lại?
b) Giữa sáu thành phố trên, có tất cả bao nhiêu đường bay của hãng X?
c) Có thể giải đáp thắc mắc ở Hoạt động khởi động không?
Phương pháp giải:
Quan sát hình 1 để trả lời câu hỏi
Lời giải chi tiết:
a) Quan sát sơ đồ ở Hình 1, ta thấy:
⦁ Có 1 đường bay từ thành phố A đến thành phố B;
⦁ Có 1 đường bay từ thành phố A đến thành phố D;
⦁ Có 1 đường bay từ thành phố A đến thành phố E;
⦁ Có 1 đường bay từ thành phố A đến thành phố F.
Vậy từ thành phố A, hãng X có tất cả 4 đường bay đến năm thành phố còn lại.
b)Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố B đến thành phố A đã được tính vào đường bay từ thành phố A đến thành phố B.
Do đó từ thành phố B, hãng X có thêm:
⦁ 1 đường bay đến thành phố C;
⦁ 1 đường bay đến thành phố D;
⦁ 1 đường bay đến thành phố F.
Khi đó, từ thành phố B, hãng X có thêm 3 đường bay đến năm thành phố còn lại.
Tương tự như vậy, ta được:
– Từ thành phố C, hãng X có thêm 2 đường bay đến năm thành phố còn lại;
– Từ thành phố D, hãng X có thêm 1 đường bay đến năm thành phố còn lại;
– Từ thành phố E, hãng X có thêm 1 đường bay đến năm thành phố còn lại.
Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố F đến năm thành phố còn lại đã được tính vào các đường bay kể trên.
Vậy giữa sáu thành phố trên, có tất cả 4 + 3 + 2 + 1 + 1 = 11 đường bay của hãng X.
Chú ý: Ngoài cách trên, ta có thể đếm số đường cong và đường thẳng (thể hiện đường bay) trên Hình 1 (hoặc Bảng 1) để kết luận về số đường bay của hãng X.
c) Ta có thể giải đáp thắc mắc ở Hoạt động khởi động như sau:
Bước 1: Từ thành phố A bay đến thành phố B;
Bước 2: Từ thành phố B bay đến thành phố C;
Bước 3: Từ thành phố C bay đến thành phố D;
Bước 4: Từ thành phố D bay đến thành phố F;
Bước 5: Từ thành phố F bay đến thành phố E;
Bước 6: Từ thành phố E bay về thành phố A.
Vậy từ thành phố A, ta có thể thăm năm thành phố B, C, D, E và F bằng các chuyến bay của hãng X sao cho mỗi thành phố chỉ qua đúng một lần, rồi quay trở về A.
Chú ý: Ta có thể thay đổi thứ tự bay đến các thành phố chỉ cần hãng X có chuyến bay giữa hai thành phố liền kề.
Cho đồ thị G như Hình 5.
a) Chỉ ra các đỉnh, các cạnh, số đỉnh, số cạnh của G.
b) Chỉ ra các đỉnh kề đỉnh D, các đỉnh kề đỉnh B.
c) Đồ thị G có đỉnh cô lập không?
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
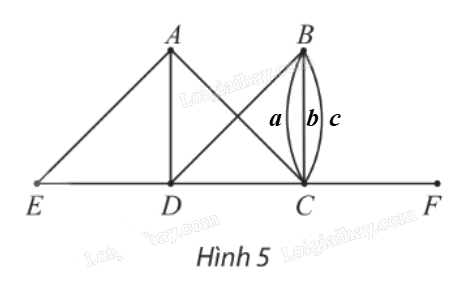
a) Các đỉnh của đồ thị G là: A, B, C, D, E và F. Đồ thị có 6 đỉnh.
Các cạnh của đồ thị G là: AC, AD, AE, a, b, c, BD, CD, CF, DE. Đồ thị có 10 cạnh.
b) Các đỉnh kề đỉnh D là: A, B, C, E.
Các đỉnh kề đỉnh B là: C, D.
c) Đồ thị G không có đỉnh cô lập.
Một mạng cục bộ có bảy máy tính 1; 2; 3; 4; 5; 6 và 7. Bảng 2 cho biết giữa mỗi cặp máy tính có kết nối trực tiếp với nhau hay không (dấu ✔ là có kết nối, dấu ✘ là không kết nối). Hãy vẽ đồ thị biểu diễn sự kết nối giữa các máy tính của mạng này.
Phương pháp giải:
Dựa vào bảng 2 để vẽ đồ thị
Lời giải chi tiết:
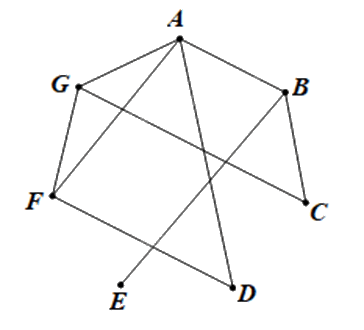
Ta vẽ đồ thị G có 7 đỉnh A, B, C, D, E, F, G lần lượt biểu diễn bảy máy tính 1; 2; 3; 4; 5; 6 và 7.
Hai đỉnh được nối bằng một cạnh nếu giữa hai máy tính có kết nối trực tiếp với nhau.
Ta có đồ thị G như sau:
Giải bài 1 trang 44, 45, 46 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan
Bài 1 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về dãy số, cấp số cộng, cấp số nhân. Đây là nền tảng quan trọng cho các kiến thức nâng cao hơn trong chương trình học. Bài tập yêu cầu học sinh vận dụng các công thức, tính chất của dãy số để giải quyết các bài toán thực tế.
Nội dung chi tiết bài giải
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 1 trang 44, 45, 46, Tusach.vn xin trình bày chi tiết lời giải cho từng phần của bài tập:
Câu a: (Trang 44)
Đề bài: (Giả sử đề bài là tìm số hạng thứ n của một dãy số)
Lời giải:
- Bước 1: Xác định loại dãy số (cấp số cộng, cấp số nhân, hay dãy số khác).
- Bước 2: Tìm số hạng đầu (u1) và công sai (d) hoặc công bội (q).
- Bước 3: Áp dụng công thức tổng quát của dãy số để tìm số hạng thứ n:
Ví dụ: Nếu là cấp số cộng, công thức là: un = u1 + (n - 1)d
Câu b: (Trang 45)
Đề bài: (Giả sử đề bài là tính tổng n số hạng đầu của một cấp số cộng)
Lời giải:
- Bước 1: Xác định số hạng đầu (u1), công sai (d) và số lượng số hạng (n).
- Bước 2: Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng:
Ví dụ: Sn = (n/2) * [2u1 + (n - 1)d]
Câu c: (Trang 46)
Đề bài: (Giả sử đề bài là tìm số hạng tổng quát của một dãy số đặc biệt)
Lời giải:
Trong trường hợp này, cần phân tích cấu trúc của dãy số để tìm ra quy luật và xây dựng công thức tổng quát. Có thể sử dụng phương pháp quy nạp toán học để chứng minh công thức.
Lưu ý khi giải bài tập
- Đọc kỹ đề bài và xác định yêu cầu của bài toán.
- Phân tích đề bài để tìm ra các thông tin cần thiết.
- Vận dụng các công thức, tính chất của dãy số một cách linh hoạt.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng học sinh
Tusach.vn luôn nỗ lực cung cấp tài liệu học tập chất lượng, đáp ứng nhu cầu của học sinh. Ngoài giải bài tập, chúng tôi còn cung cấp các bài giảng, video hướng dẫn và các tài liệu ôn tập hữu ích khác. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng tổng hợp công thức quan trọng
| Công thức | Mô tả |
|---|---|
| un = u1 + (n - 1)d | Số hạng thứ n của cấp số cộng |
| Sn = (n/2) * [2u1 + (n - 1)d] | Tổng n số hạng đầu của cấp số cộng |
| un = u1 * q(n-1) | Số hạng thứ n của cấp số nhân |
| Sn = u1 * (1 - qn) / (1 - q) | Tổng n số hạng đầu của cấp số nhân (q ≠ 1) |