Giải bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và củng cố kiến thức về chủ đề đã học. Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh tự tin giải bài tập và nắm vững kiến thức.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo.
Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.
Đề bài
Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.
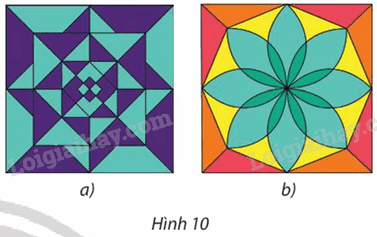
Phương pháp giải - Xem chi tiết
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết
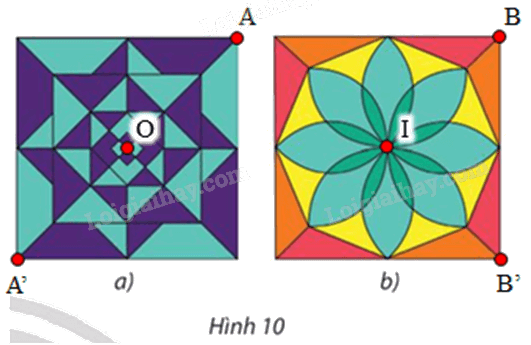
⦁ Hình 10a:
Hình vẽ có dạng hình vuông, gọi O là tâm hình vuông đó và A là 1 đỉnh của hình vuông.
Phép quay tâm O, góc quay 180° biến điểm A thành điểm A’.
Tương tự, ta chọn các điểm khác bất kì trên Hình 10a.
Khi đó qua phép quay tâm O, góc quay 180° ta cũng xác định được ảnh của các điểm đó trên Hình 10a ban đầu.
Vậy phép quay biến Hình 10a thành chính nó là phép quay tâm O, góc quay 180°.
Ngoài ra, phép quay tâm O, góc quay –180° cũng biến Hình 10a thành chính nó.
⦁ Hình 10b:
Hình vẽ có dạng hình vuông, gọi I là tâm hình vuông đó và B là 1 đỉnh của hình vuông.
Phép quay tâm I, góc quay 90° biến điểm B thành điểm B’.
Tương tự, ta chọn các điểm khác bất kì trên hình 10b.
Khi đó qua phép quay tâm I, góc quay 90° ta cũng xác định được ảnh của các điểm đó trên Hình 10b ban đầu.
Vậy phép quay biến Hình 10b thành chính nó là phép quay tâm I, góc quay 90°.
Chú ý: Có nhiều phép quay biến Hình 10a thành chính nó, chẳng hạn ngoài phép quay ở trên, ta có thể kể đến phép quay tâm I, góc quay 180° hoặc phép quay tâm I, góc quay –90°, …
Giải bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm, định lý và công thức liên quan đến chủ đề đang xét.
Nội dung bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Để giải quyết bài 4 trang 29 một cách hiệu quả, trước tiên chúng ta cần xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu chúng ta:
- Phân tích đề bài và xác định các yếu tố quan trọng.
- Lựa chọn phương pháp giải phù hợp.
- Thực hiện các phép tính và biến đổi toán học.
- Kiểm tra lại kết quả và đảm bảo tính chính xác.
Lời giải chi tiết bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Dưới đây là lời giải chi tiết cho bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng và dễ hiểu, kèm theo các giải thích chi tiết để giúp các em học sinh nắm vững kiến thức.
(Giả sử bài toán cụ thể là: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.)
- Tìm tọa độ đỉnh của parabol:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c, với a = 1, b = -4, c = 3.
Hoành độ đỉnh của parabol là x0 = -b / (2a) = -(-4) / (2 * 1) = 2.
Tung độ đỉnh của parabol là y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = -1.
Vậy tọa độ đỉnh của parabol là (2; -1).
- Vẽ đồ thị hàm số:
Xác định một vài điểm thuộc đồ thị hàm số, ví dụ:
- Khi x = 0, y = 3.
- Khi x = 1, y = 0.
- Khi x = 3, y = 0.
- Khi x = 4, y = 3.
Vẽ parabol đi qua các điểm đã xác định và có đỉnh là (2; -1).
Mẹo giải bài tập Toán 11 Chân trời sáng tạo hiệu quả
Để giải bài tập Toán 11 Chân trời sáng tạo một cách hiệu quả, các em học sinh nên:
- Nắm vững các khái niệm, định lý và công thức cơ bản.
- Luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
- Sử dụng các phương pháp giải phù hợp.
- Kiểm tra lại kết quả và đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn là website cung cấp lời giải bài tập Toán 11 Chân trời sáng tạo nhanh chóng, chính xác và dễ hiểu. Chúng tôi luôn cập nhật các lời giải mới nhất và cung cấp các tài liệu học tập hữu ích để giúp các em học sinh học tập tốt hơn. Hãy truy cập Tusach.vn để được hỗ trợ ngay hôm nay!
| Chủ đề | Liên kết |
|---|---|
| Giải bài tập Toán 11 Chân trời sáng tạo | Tusach.vn/toan-11-chan-troi-sang-tao |
| Chuyên đề học tập Toán 11 | Tusach.vn/chuyen-de-toan-11 |