Giải bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Tổng quan nội dung
Giải bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của các bạn.
Gọi O được gọi là tâm đối xứng quay bậc (n{rm{ }}(n in mathbb{N}*)) của hình ℋ nếu sau khi thực hiện phép quay ({Q_{left( {O,frac{{360^circ }}{n}} right)}})
Đề bài
Gọi O được gọi là tâm đối xứng quay bậc \(n{\rm{ }}(n \in \mathbb{N}*)\) của hình ℋ nếu sau khi thực hiện phép quay \({Q_{\left( {O,\frac{{360^\circ }}{n}} \right)}}\) ta lại được chính hình ℋ. Hình có tâm đối xứng quay bậc n gọi là hình đối xứng quay bậc n. Tìm các hình đối xứng quay trong Hình 2.
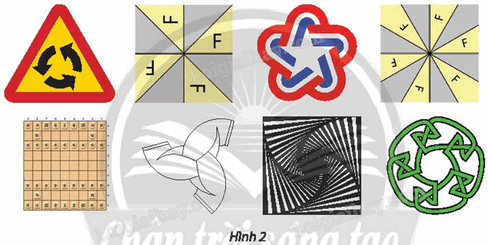
Phương pháp giải - Xem chi tiết
Quan sát hình 2, suy luận để trả lời
Lời giải chi tiết
Ta đặt tên cho các hình vẽ trong Hình 2 theo thứ tự từ trái qua phải, từ trên xuống dưới là: a, b, c, d, e, f, g, h.
⦁ Xét Hình 2a: biển báo có dạng hình tam giác đều.

Gọi O là tâm đường tròn ngoại tiếp tam giác, điểm A là một đỉnh của tam giác.
Phép quay tâm O, góc quay 120° biến điểm A thành điểm A’.
Khi đó ta thấy điểm A’ nằm trên Hình 2a ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2a.
Khi đó qua phép quay tâm O, góc quay 120°, ta cũng xác định được ảnh của các điểm đó trên Hình 2a ban đầu.
Vì vậy phép quay biến Hình 2a thành chính nó là phép quay tâm O, góc quay 120°.
Ta có \(\frac{{360^\circ }}{n} = 120^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}3 \in \mathbb{N}*.\)
Vì vậy Hình 2a có tâm đối xứng quay bậc 3.
⦁ Xét Hình 2b: có dạng hình vuông.
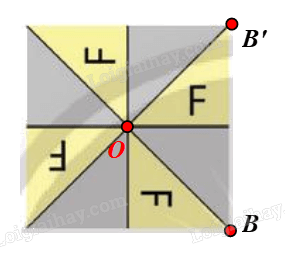
Gọi O là tâm hình vuông và B là một đỉnh của hình vuông.
Phép quay tâm O, góc quay 90° biến điểm B thành điểm B’.
Khi đó ta thấy điểm B’ nằm trên Hình 2b ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2b.
Khi đó qua phép quay tâm O, góc quay 90°, ta cũng xác định được ảnh của các điểm đó trên Hình 2b ban đầu.
Vì vậy phép quay biến Hình 2b thành chính nó là phép quay tâm O, góc quay 90°.
Ta có \(\frac{{360^\circ }}{n} = 90^\circ \) Suy ra \(n{\rm{ }} = {\rm{ }}4 \in \mathbb{N}*.\)
Vì vậy Hình 2b có tâm đối xứng quay bậc 4.
⦁ Xét Hình 2c:

Chọn hai điểm O, C như hình vẽ.
Phép quay tâm O, góc quay 72° biến điểm C thành điểm C’.
Khi đó ta thấy điểm C’ nằm trên Hình 2c ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2c.
Khi đó qua phép quay tâm O, góc quay 72°, ta cũng xác định được ảnh của các điểm đó trên Hình 2c ban đầu.
Vì vậy phép quay biến Hình 2c thành chính nó là phép quay tâm O, góc quay 72°.
Ta có \(\frac{{360^\circ }}{n} = 72^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}5 \in \mathbb{N}*.\)
Vì vậy Hình 2c có tâm đối xứng quay bậc 5.
⦁ Xét Hình 2d: có dạng hình vuông
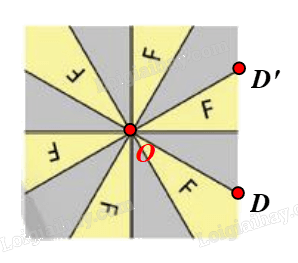
Gọi O là tâm hình vuông. Chọn điểm D như hình vẽ.
Phép quay tâm O, góc quay 60° biến điểm D thành điểm D’.
Khi đó ta thấy điểm D’ nằm trên Hình 2d ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2d.
Khi đó qua phép quay tâm O, góc quay 60°, ta cũng xác định được ảnh của các điểm đó trên Hình 2d ban đầu.
Vì vậy phép quay biến Hình 2d thành chính nó là phép quay tâm O, góc quay 60°.
Ta có \(\frac{{360^\circ }}{n} = 60^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}6 \in \mathbb{N}*.\)
Vì vậy Hình 2d có tâm đối xứng quay bậc 6.
⦁ Xét Hình 2e: có dạng hình vuông.
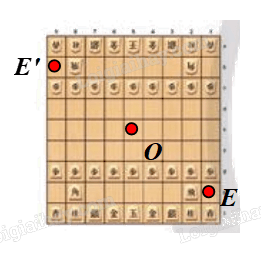
Gọi O là tâm hình vuông. Chọn điểm E như hình vẽ.
Phép quay tâm O, góc quay 180° biến điểm E thành điểm E’.
Khi đó ta thấy điểm E’ nằm trên Hình 2e ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2e.
Khi đó qua phép quay tâm O, góc quay 180°, ta cũng xác định được ảnh của các điểm đó trên Hình 2e ban đầu.
Vì vậy phép quay biến Hình 2e thành chính nó là phép quay tâm O, góc quay 180°.
Ta có \(\frac{{360^\circ }}{n} = 180^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}2 \in \mathbb{N}*.\)
Vì vậy Hình 2e có tâm đối xứng quay bậc 2.
⦁ Xét Hình 2f:
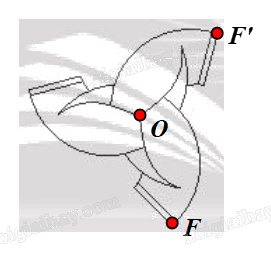
Chọn hai điểm O, F như hình vẽ.
Phép quay tâm O, góc quay 120° biến điểm F thành điểm F’.
Khi đó ta thấy điểm F’ nằm trên Hình 2f ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2f.
Khi đó qua phép quay tâm O, góc quay 120°, ta cũng xác định được ảnh của các điểm đó trên Hình 2f ban đầu.
Vì vậy phép quay biến Hình 2f thành chính nó là phép quay tâm O, góc quay 120°.
Ta có \(\frac{{360^\circ }}{n} = 120^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}3 \in \mathbb{N}*.\)
Vì vậy Hình 2f có tâm đối xứng quay bậc 3.
⦁ Xét Hình 2g: có dạng hình vuông.
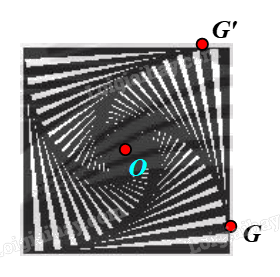
Gọi O là tâm hình vuông. Chọn điểm G như hình vẽ.
Phép quay tâm O, góc quay 90° biến điểm G thành điểm G’.
Khi đó ta thấy điểm G’ nằm trên Hình 2g ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2g.
Khi đó qua phép quay tâm O, góc quay 90°, ta cũng xác định được ảnh của các điểm đó trên Hình 2g ban đầu.
Vì vậy phép quay biến Hình 2g thành chính nó là phép quay tâm O, góc quay 90°.
Ta có \(\frac{{360^\circ }}{n} = 90^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}4 \in \mathbb{N}*.\)
Vì vậy Hình 2g có tâm đối xứng quay bậc 4.
⦁ Xét Hình 2h: có dạng hình tròn
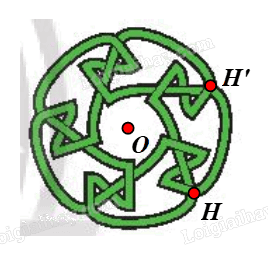
Gọi O là tâm hình tròn. Chọn điểm H như hình vẽ.
Phép quay tâm O, góc quay 72° biến điểm H thành điểm H’.
Khi đó ta thấy điểm H’ nằm trên Hình 2h ban đầu.
Tương tự, ta chọn các điểm khác bất kì trên Hình 2h.
Khi đó qua phép quay tâm O, góc quay 72°, ta cũng xác định được ảnh của các điểm đó trên Hình 2h ban đầu.
Vì vậy phép quay biến Hình 2h thành chính nó là phép quay tâm O, góc quay 72°.
Ta có \(\frac{{360^\circ }}{n} = 72^\circ \). Suy ra \(n{\rm{ }} = {\rm{ }}5 \in \mathbb{N}*.\)
Vì vậy Hình 2h có tâm đối xứng quay bậc 5.
Vậy tất cả các hình trong Hình 2 đều là hình đối xứng quay có bậc lần lượt là 3; 4; 5; 6; 2; 3; 4; 5 (tính thứ tự các hình từ trái qua phải và từ trên xuống dưới).
Giải bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp giải
Bài 16 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải:
- Tính đạo hàm của hàm số.
- Tìm cực trị của hàm số.
- Khảo sát sự biến thiên của hàm số.
- Giải các bài toán liên quan đến ứng dụng của đạo hàm (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước).
Nội dung chi tiết bài 16 trang 42
Để giải quyết bài 16 trang 42 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
- Định nghĩa đạo hàm: Đạo hàm của hàm số f(x) tại điểm x0 được định nghĩa là giới hạn của tỷ số giữa độ biến thiên của hàm số và độ biến thiên của đối số khi độ biến thiên của đối số tiến tới 0.
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, quy tắc đạo hàm của hàm hợp.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
- Ứng dụng của đạo hàm: Tìm cực trị của hàm số, khảo sát sự biến thiên của hàm số, giải các bài toán tối ưu.
Lời giải chi tiết bài 16 trang 42 (Ví dụ)
(Giả sử bài 16 yêu cầu khảo sát hàm số y = x3 - 3x2 + 2)
Bước 1: Tìm tập xác định của hàm số.
Hàm số y = x3 - 3x2 + 2 xác định trên tập số thực R.
Bước 2: Tính đạo hàm cấp nhất.
y' = 3x2 - 6x
Bước 3: Tìm điểm dừng.
y' = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Bước 4: Lập bảng biến thiên.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | ĐC | TC |
Bước 5: Kết luận.
Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0, yCĐ = 2 và đạt cực tiểu tại x = 2, yCT = -2.
Mẹo giải bài tập đạo hàm hiệu quả
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
- Tham khảo các tài liệu tham khảo, sách giáo khoa, và các trang web học tập uy tín.
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 11 Chân trời sáng tạo. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kiến thức của bạn!