Giải mục 3 trang 75, 76, 77, 78, 79 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 75, 76, 77, 78, 79 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 75, 76, 77, 78, 79 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và giải quyết các bài tập một cách hiệu quả.
Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em tự tin hơn khi làm bài tập về nhà và chuẩn bị cho các kỳ thi sắp tới.
Cho hình hộp chữ nhật (OABC.{O_1}{A_1}{B_1}{C_1}.)
Khám phá 4
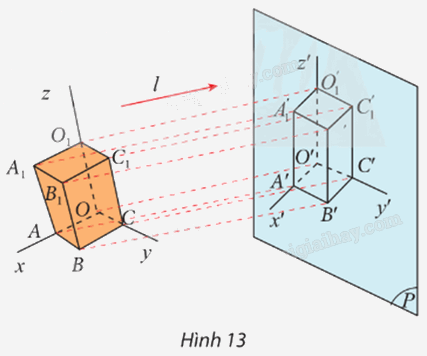
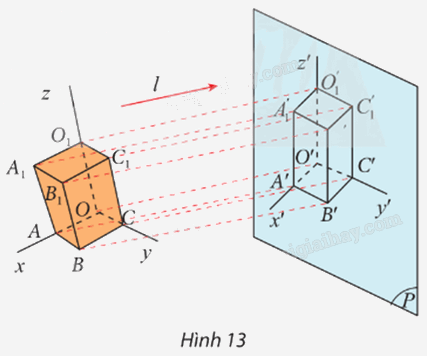
Cho hình hộp chữ nhật \(OABC.{O_1}{A_1}{B_1}{C_1}.\) Ba tia Ox, Oy, Oz lần lượt chứa ba cạnh OA, OC, OO1. Cho mặt phẳng (P) và đường thẳng l không song song với (P). Tìm ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
Phương pháp giải:
Để tìm ảnh của hình ta tìm ảnh của từng điểm qua phép chiếu song song theo phương l lên mặt phẳng (P).
Lời giải chi tiết:
– Ta có OO’ // l và \(O' \in \left( P \right).\)
Suy ra O’ là ảnh của O qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được A’, B’, C’, lần lượt là ảnh của A, B, C, O1, A1, B1, C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
Do đó là ảnh của hình hộp chữ nhật OABC.O1A1B1C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
– Ta có O’, A’ lần lượt là ảnh của O, A qua phép chiếu song song theo phương l lên mặt phẳng (P).
Suy ra O’A’ là ảnh của OA qua phép chiếu song song theo phương l lên mặt phẳng (P).
Mà A’ ∈ O’x’.
Do đó O’x’ là ảnh của Ox qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được O’y’, O’z’ lần lượt là ảnh của Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
Vậy ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P) lần lượt là hình hộp chữ nhật và các tia O’x’, O’y’, O’z’.
Vận dụng 3
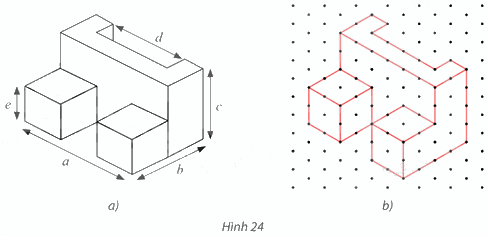
Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a có hình biểu diễn được vẽ trên giấy kẻ ô li là Hình 24b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm.
Phương pháp giải:
Quan sát hình 24 để trả lời
Lời giải chi tiết:
Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a được biểu diễn trên Hình 24b như sau:
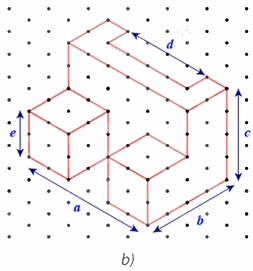
Do mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm nên ta có:
Chiều dài a = 6 cm; chiều rộng b = 4 cm; chiều cao c = 4 cm; bề dày d = 4 cm; bề dày e = 2 cm.
Khám phá 5
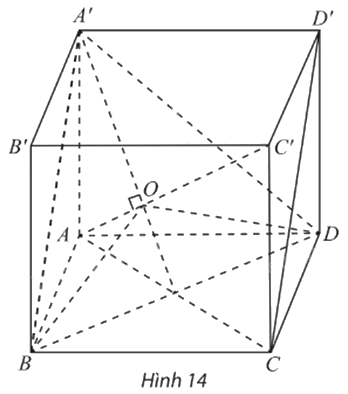
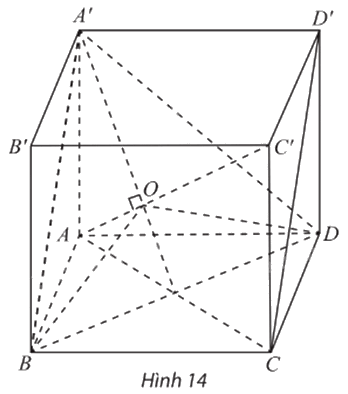
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng đơn vị (Hình 14).
a) Chỉ ra rằng \(AC' \bot \left( {A'BD} \right).\)
b) Gọi O là tâm của tam giác đều A’BD. Hình chiếu vuông góc của ba đoạn AB, AD và AA’ lên (A’BD) có bằng nhau không?
c) Chỉ ra rằng \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
Phương pháp giải:
Để chứng minh đường thẳng \(d \bot (P)\) ta chứng minh d vuông góc với 2 đường thẳng cắt nhau nằm trong (P).
Lời giải chi tiết:
a) Ta có \(A'D \bot AD'\) (AA’D’D là hình vuông) và \(A'D \bot C'D'{\rm{ }}(C'D' \bot \left( {AA'D'D} \right)).\) Suy ra \(A'D \bot \left( {AC'D'} \right).\)
Do đó \(A'D \bot AC'{\rm{ }}\left( 1 \right)\)
Chứng minh tương tự, ta được \(A'B \bot AC'{\rm{ }}\left( 2 \right)\)
Từ (1), (2), ta thu được \(AC' \bot \left( {A'BD} \right).\)
b) Gọi M là trung điểm BD.
Ta có AB = AD (do ABCD là hình vuông).
Suy ra tam giác ABD cân tại A.
Do đó AM ⊥ BD.
Lại có O là tâm của tam giác đều A’BD.
Suy ra \(A'M \bot BD\) và \(O \in A'M\).
Ta có \(AM \bot BD\) và \(A'M \bot BD\) (chứng minh trên).
Suy ra \(BD \bot \left( {AA'M} \right).\)
Do đó \(BD \bot AO{\rm{ }}\left( 3 \right)\)
Chứng minh tương tự, ta được \(A'D \bot AO{\rm{ }}\left( 4 \right)\)
Từ (3), (4), suy ra \(AO \bot \left( {A'BD} \right).\)
Khi đó O là hình chiếu vuông góc của A lên mặt phẳng (A’BD).
Mà B là hình chiếu vuông góc của B lên mặt phẳng (A’BD).
Suy ra OB là hình chiếu vuông góc của AB lên mặt phẳng (A’BD).
Chứng minh tương tự, ta được: OD, OA’ lần lượt là hình chiếu vuông góc của AD, AA’ lên mặt phẳng (A’BD).
Tam giác A’BD đều có tâm O.
Suy ra OA’ = OB = OD.
Vậy hình chiếu vuông góc OB, OD và OA’ lần lượt của ba đoạn AB, AD và AA’ lên (A’BD) có độ dài bằng nhau.
c) Ta có tam giác A’BD đều. Suy ra \(\widehat {BA'D} = 60^\circ \)
Tam giác A’BD đều có tâm O. Suy ra O là tâm đường tròn ngoại tiếp tam giác A’BD.
Khi đó \(\widehat {BOD} = 2\widehat {BA'D} = 2.60^\circ = 120^\circ \)
Chứng minh tương tự, ta được \(\widehat {DOA'} = 120^\circ \) và \(\widehat {A'OB} = 120^\circ \)
Vậy \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
- Khám phá 4
- Khám phá 5
- Thực hành 3
- Vận dụng 3
Cho hình hộp chữ nhật \(OABC.{O_1}{A_1}{B_1}{C_1}.\) Ba tia Ox, Oy, Oz lần lượt chứa ba cạnh OA, OC, OO1. Cho mặt phẳng (P) và đường thẳng l không song song với (P). Tìm ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
Phương pháp giải:
Để tìm ảnh của hình ta tìm ảnh của từng điểm qua phép chiếu song song theo phương l lên mặt phẳng (P).
Lời giải chi tiết:
– Ta có OO’ // l và \(O' \in \left( P \right).\)
Suy ra O’ là ảnh của O qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được A’, B’, C’, lần lượt là ảnh của A, B, C, O1, A1, B1, C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
Do đó là ảnh của hình hộp chữ nhật OABC.O1A1B1C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
– Ta có O’, A’ lần lượt là ảnh của O, A qua phép chiếu song song theo phương l lên mặt phẳng (P).
Suy ra O’A’ là ảnh của OA qua phép chiếu song song theo phương l lên mặt phẳng (P).
Mà A’ ∈ O’x’.
Do đó O’x’ là ảnh của Ox qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được O’y’, O’z’ lần lượt là ảnh của Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
Vậy ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P) lần lượt là hình hộp chữ nhật và các tia O’x’, O’y’, O’z’.
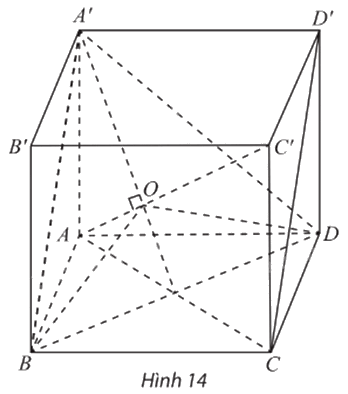
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng đơn vị (Hình 14).
a) Chỉ ra rằng \(AC' \bot \left( {A'BD} \right).\)
b) Gọi O là tâm của tam giác đều A’BD. Hình chiếu vuông góc của ba đoạn AB, AD và AA’ lên (A’BD) có bằng nhau không?
c) Chỉ ra rằng \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
Phương pháp giải:
Để chứng minh đường thẳng \(d \bot (P)\) ta chứng minh d vuông góc với 2 đường thẳng cắt nhau nằm trong (P).
Lời giải chi tiết:
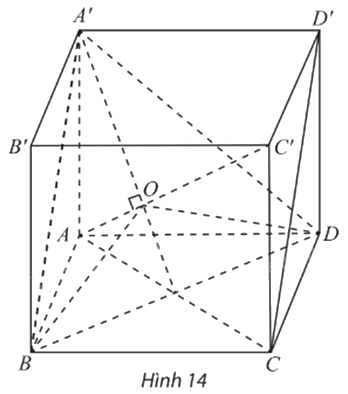
a) Ta có \(A'D \bot AD'\) (AA’D’D là hình vuông) và \(A'D \bot C'D'{\rm{ }}(C'D' \bot \left( {AA'D'D} \right)).\) Suy ra \(A'D \bot \left( {AC'D'} \right).\)
Do đó \(A'D \bot AC'{\rm{ }}\left( 1 \right)\)
Chứng minh tương tự, ta được \(A'B \bot AC'{\rm{ }}\left( 2 \right)\)
Từ (1), (2), ta thu được \(AC' \bot \left( {A'BD} \right).\)
b) Gọi M là trung điểm BD.
Ta có AB = AD (do ABCD là hình vuông).
Suy ra tam giác ABD cân tại A.
Do đó AM ⊥ BD.
Lại có O là tâm của tam giác đều A’BD.
Suy ra \(A'M \bot BD\) và \(O \in A'M\).
Ta có \(AM \bot BD\) và \(A'M \bot BD\) (chứng minh trên).
Suy ra \(BD \bot \left( {AA'M} \right).\)
Do đó \(BD \bot AO{\rm{ }}\left( 3 \right)\)
Chứng minh tương tự, ta được \(A'D \bot AO{\rm{ }}\left( 4 \right)\)
Từ (3), (4), suy ra \(AO \bot \left( {A'BD} \right).\)
Khi đó O là hình chiếu vuông góc của A lên mặt phẳng (A’BD).
Mà B là hình chiếu vuông góc của B lên mặt phẳng (A’BD).
Suy ra OB là hình chiếu vuông góc của AB lên mặt phẳng (A’BD).
Chứng minh tương tự, ta được: OD, OA’ lần lượt là hình chiếu vuông góc của AD, AA’ lên mặt phẳng (A’BD).
Tam giác A’BD đều có tâm O.
Suy ra OA’ = OB = OD.
Vậy hình chiếu vuông góc OB, OD và OA’ lần lượt của ba đoạn AB, AD và AA’ lên (A’BD) có độ dài bằng nhau.
c) Ta có tam giác A’BD đều. Suy ra \(\widehat {BA'D} = 60^\circ \)
Tam giác A’BD đều có tâm O. Suy ra O là tâm đường tròn ngoại tiếp tam giác A’BD.
Khi đó \(\widehat {BOD} = 2\widehat {BA'D} = 2.60^\circ = 120^\circ \)
Chứng minh tương tự, ta được \(\widehat {DOA'} = 120^\circ \) và \(\widehat {A'OB} = 120^\circ \)
Vậy \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
Vẽ trên giấy kẻ ô li hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 (quy tắc mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm).
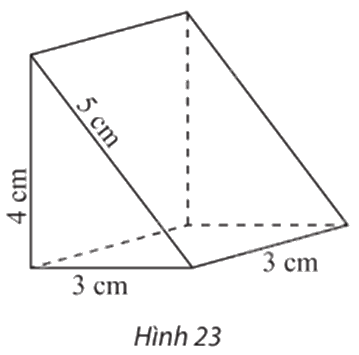
Phương pháp giải:
Hình biểu diễn của một hình khối H trong không gian là hình chiếu song song hoặc vuông góc của H lên mặt phẳng.
Lời giải chi tiết:
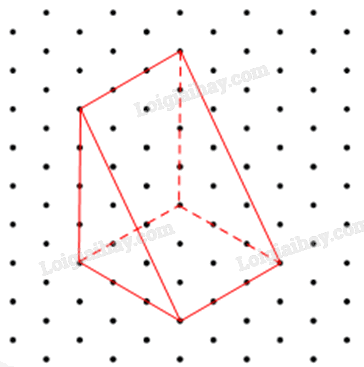
Hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 là:

Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a có hình biểu diễn được vẽ trên giấy kẻ ô li là Hình 24b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm.
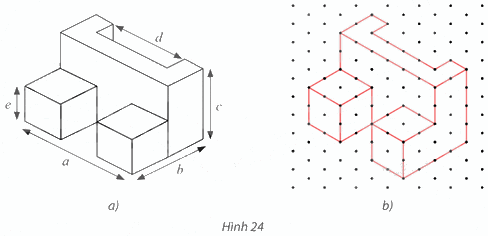
Phương pháp giải:
Quan sát hình 24 để trả lời
Lời giải chi tiết:
Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a được biểu diễn trên Hình 24b như sau:
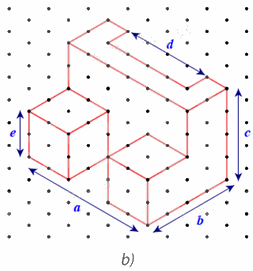
Do mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm nên ta có:
Chiều dài a = 6 cm; chiều rộng b = 4 cm; chiều cao c = 4 cm; bề dày d = 4 cm; bề dày e = 2 cm.
Thực hành 3
Vẽ trên giấy kẻ ô li hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 (quy tắc mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm).
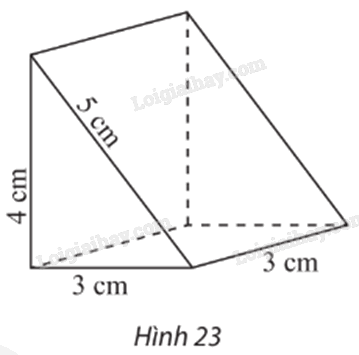
Phương pháp giải:
Hình biểu diễn của một hình khối H trong không gian là hình chiếu song song hoặc vuông góc của H lên mặt phẳng.
Lời giải chi tiết:
Hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 là:
Giải mục 3 trang 75, 76, 77, 78, 79 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan
Mục 3 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để đạt kết quả tốt. Tusach.vn sẽ giúp bạn làm điều đó.
Nội dung chi tiết giải bài tập
Chúng ta sẽ đi vào giải chi tiết từng bài tập từ trang 75 đến trang 79. Mỗi bài giải sẽ bao gồm:
- Phân tích đề bài: Xác định rõ yêu cầu của đề bài, các dữ kiện đã cho và những gì cần tìm.
- Lý thuyết liên quan: Nhắc lại các kiến thức lý thuyết cần thiết để giải bài tập.
- Phương pháp giải: Trình bày các bước giải cụ thể, rõ ràng, dễ hiểu.
- Đáp án: Cung cấp đáp án chính xác và giải thích tại sao đáp án đó lại đúng.
Giải trang 75
Bài 1: (Đề bài cụ thể)...
Giải:...
Bài 2: (Đề bài cụ thể)...
Giải:...
Giải trang 76
Bài 3: (Đề bài cụ thể)...
Giải:...
Giải trang 77
Bài 4: (Đề bài cụ thể)...
Giải:...
Giải trang 78
Bài 5: (Đề bài cụ thể)...
Giải:...
Giải trang 79
Bài 6: (Đề bài cụ thể)...
Giải:...
Mẹo học tập hiệu quả
Để học tốt Toán 11 Chân trời sáng tạo, bạn nên:
- Nắm vững lý thuyết: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các công thức và định lý.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô, bạn bè hoặc tìm kiếm trên các trang web học tập uy tín như tusach.vn.
- Sử dụng sơ đồ tư duy: Sơ đồ tư duy giúp bạn hệ thống hóa kiến thức và dễ dàng ghi nhớ hơn.
Bảng tổng hợp công thức quan trọng (Ví dụ)
| Công thức | Mô tả |
|---|---|
| Công thức A | Giải thích công thức A |
| Công thức B | Giải thích công thức B |
Kết luận
Hy vọng với lời giải chi tiết và những lời khuyên hữu ích trên, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 11 Chuyên đề học tập - Chân trời sáng tạo. Tusach.vn luôn là người bạn đồng hành đáng tin cậy của các em trên con đường chinh phục tri thức.