Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học. Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự tin giải bài tập và nắm vững kiến thức.

Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách Chuyên đề học tập Toán 11 Chân trời sáng tạo.

Tìm phép biến hình f biến hình (A) thành hình (B).

Đề bài

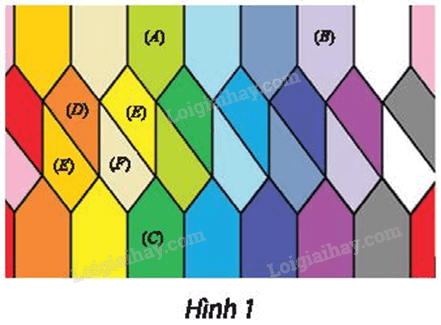
Cho Hình 1.

a) Tìm phép biến hình f biến hình (A) thành hình (B).

b) Tìm phép biến hình g biến hình (A) thành hình (C).

c) Tìm các phép biến hình biến hình (D) thành lần lượt các hình (E), (F), (G).

Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo 2

Quan sát hình 1 và dựa vào các phép biến hình đã học để làm

Lời giải chi tiết

a) Gọi I là một điểm trên hình (A) và I’ là một điểm trên hình (B) có vị trí tương ứng với điểm I trên hình (A) (hình vẽ).

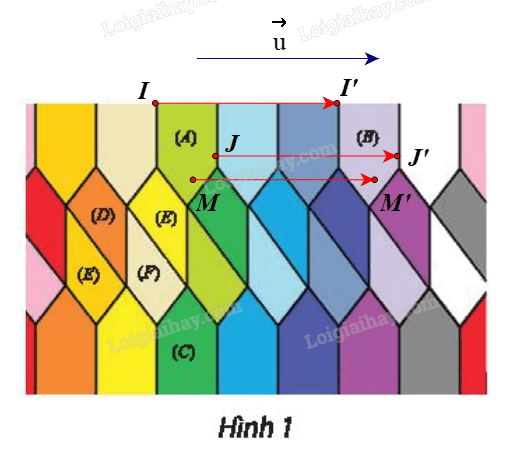
Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo 3

Giả sử là vectơ có phương vuông góc với trục đối xứng của hình (A), độ dài bằng độ dài từ điểm I đến điểm I’ (hình vẽ).

Tức là, \(\vec u = \overrightarrow {II'} \)

Gọi J là một điểm bất kì trên hình (A).

Lấy điểm J’ sao cho \(\overrightarrow {JJ'} = \vec u\)

Khi đó J’ là một điểm trên hình (B) có vị trí tương ứng với điểm J trên hình (A).

Tương tự như vậy, với mỗi điểm M bất kì trên hình (A), ta lấy điểm M’ sao cho \(\overrightarrow {MM'} = \vec u\) thì ta được tập hợp các điểm M’ tạo thành hình (B).

Vậy phép biến hình f cần tìm là phép tịnh tiến theo .

b) Chọn đường thẳng d như hình vẽ.

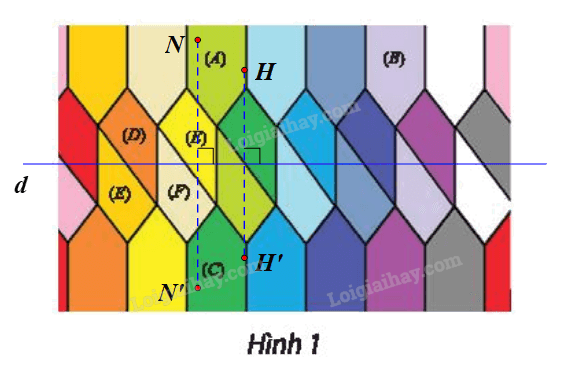
Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo 4

Lấy điểm H bất kì nằm trên hình (A).

Ta đặt \(H'{\rm{ }} = {\rm{ }}{Đ_d}\left( H \right).\)

Khi đó H’ nằm trên hình (C) có vị trí tương ứng với điểm H trên hình (A).

Tương tự như vậy, với mỗi điểm N bất kì trên hình (A), ta lấy điểm N’ sao cho \(N'{\rm{ }} = {\rm{ }}{Đ_d}\left( N \right)\) thì ta được tập hợp các điểm N’ tạo thành hình (C).

Vậy phép biến hình g cần tìm là phép đối xứng trục d, với d là đường thẳng trên Hình 1 (như hình vẽ).

c) ⦁ Phép biến hình biến hình (D) thành hình (E):

Gọi R là một điểm bất kì trên hình (D).

Giả sử O là trung điểm của cạnh bên hình thang (D) (như hình vẽ).

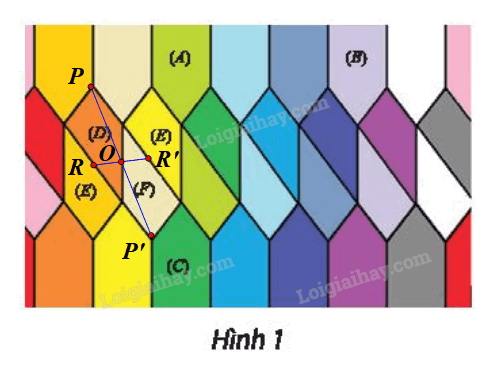
Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo 5

Lấy điểm R’ sao cho \(R' = {\rm{ }}{{\rm{D}}_O}\left( R \right).\)

Khi đó R’ là một điểm trên hình (F) có vị trí tương ứng với điểm R trên hình (D).

Tương tự như vậy, với mỗi điểm P bất kì trên hình (D), ta lấy điểm P’ sao cho \(P' = {\rm{ }}{Đ_O}\left( P \right)\) thì ta được tập hợp các điểm P’ tạo thành hình (F).

Vậy phép đối xứng tâm O biến hình (D) thành hình (F).

Giải bài 15 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan và Phương pháp giải

Bài 15 trang 42 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế, đặc biệt là các bài toán liên quan đến tối ưu hóa. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, bao gồm đạo hàm của hàm số, điều kiện cần và đủ để hàm số đạt cực trị, và cách sử dụng đạo hàm để tìm giá trị lớn nhất và nhỏ nhất của hàm số.

Nội dung chi tiết bài 15 trang 42

Bài 15 thường bao gồm các dạng bài tập sau:

Dạng 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên một khoảng cho trước. Để giải quyết dạng bài này, học sinh cần tìm đạo hàm của hàm số, xác định các điểm cực trị, và so sánh giá trị của hàm số tại các điểm cực trị và tại các đầu mút của khoảng.
Dạng 2: Giải các bài toán tối ưu hóa. Trong các bài toán tối ưu hóa, học sinh cần xây dựng hàm số biểu diễn đại lượng cần tối ưu, tìm đạo hàm của hàm số, và giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị. Sau đó, học sinh cần kiểm tra điều kiện của bài toán để xác định giá trị lớn nhất hoặc nhỏ nhất của hàm số.
Dạng 3: Ứng dụng đạo hàm để giải các bài toán thực tế. Các bài toán thực tế thường yêu cầu học sinh phải phân tích đề bài, xây dựng mô hình toán học, và sử dụng đạo hàm để giải quyết bài toán.

Lời giải chi tiết bài 15 trang 42 (Ví dụ)

Bài toán: (Giả sử đây là một bài toán cụ thể, ví dụ: Tìm giá trị lớn nhất của hàm số f(x) = -x² + 4x + 1 trên khoảng [0; 3]).

Lời giải:

Tính đạo hàm: f'(x) = -2x + 4
Tìm điểm cực trị: Giải phương trình f'(x) = 0, ta được x = 2.
Kiểm tra điều kiện: x = 2 thuộc khoảng [0; 3].
Tính giá trị của hàm số tại các điểm cực trị và đầu mút của khoảng:
- f(0) = 1
- f(2) = 5
- f(3) = 4
Kết luận: Giá trị lớn nhất của hàm số f(x) trên khoảng [0; 3] là 5, đạt được tại x = 2.

Mẹo giải bài tập hiệu quả

Để giải bài tập về đạo hàm và ứng dụng đạo hàm một cách hiệu quả, học sinh nên:

Nắm vững các định nghĩa và tính chất của đạo hàm.
Luyện tập thường xuyên các bài tập về đạo hàm.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra kết quả.
Đọc kỹ đề bài và phân tích các yếu tố quan trọng để xây dựng mô hình toán học phù hợp.

Tusach.vn – Đồng hành cùng bạn học Toán 11

Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúng tôi hy vọng rằng với sự hỗ trợ của Tusach.vn, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt nhất trong môn Toán.

Chuyên đề	Bài	Trang
Học tập	15	42

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN

Giới Thiệu
Chính Sách Bảo Mật
Liên Hệ
Blog
Email: Taisachebook@gmail.com