Giải mục 1 trang 20, 21 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 20, 21 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 20, 21 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu nhất.
Bài giải này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi.
Cho điểm O. Gọi f là quy tắc xác định như sau:
Thực hành 1
Trong mặt phẳng tọa độ Oxy, cho các điểm I(1; 1), M(2; 2), N(0; –3) và P(–1; –2). Tìm tọa độ các điểm \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right),{\rm{ }}N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right),{\rm{ }}P'{\rm{ }} = {\rm{ }}{Đ_I}\left( P \right).\)
Phương pháp giải:
Nếu thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
+ Ta có \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right).\)
Suy ra I(1; 1) là trung điểm MM’ với M(2; 2).
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M} = 2.1 - 2 = 0\\{y_{M'}} = 2{y_I} - {y_M} = 2.1 - 2 = 0\end{array} \right.\)
Suy ra M’ có tọa độ là (0; 0).
+ Ta có \(N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right).\)
Suy ra I(1; 1) là trung điểm của NN’ với N(0; –3).
Do đó \(\left\{ \begin{array}{l}{x_{N'}} = 2{x_I} - {x_N} = 2.1 - 0 = 2\\{y_{N'}} = 2{y_I} - {y_N} = 2.1 + 3 = 5\end{array} \right.\)
Suy ra N’ có tọa độ là N’(2; 5).
+ Ta có \(P' = {\rm{ }}{Đ_I}\left( P \right).\)
Suy ra I(1; 1) là trung điểm PP’ với P(–1; –2).
Do đó \(\left\{ \begin{array}{l}{x_{P'}} = 2{x_I} - {x_P} = 2.1 + 1 = 3\\{y_{P'}} = 2{y_I} - {y_P} = 2.1 + 2 = 4\end{array} \right.\)
Suy ra P’ có tọa độ là P’(3; 4).
Vậy \(M'\left( {0;{\rm{ }}0} \right),{\rm{ }}N'\left( {2;{\rm{ }}5} \right),{\rm{ }}P'\left( {3;{\rm{ }}4} \right).\)
Khám phá 1
Cho điểm O. Gọi f là quy tắc xác định như sau:
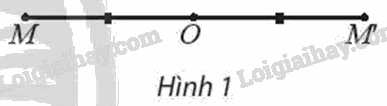
a) Với điểm M khác O, xác định điểm M’ sao cho O là trung điểm của MM’ (Hình 1).
b) Với điểm M trùng với O thì f biến điểm M thành chính nó.
Hỏi f có phải là phép biến hình không?
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
Theo đề, ta có M’ = f(M).
Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
Vận dụng 1
Tìm phép đối xứng tâm biến mỗi hình sau thành chính nó.

Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
⦁ Ta xét hình màu đỏ:

Giả sử ta chọn điểm O trên hình màu đỏ như hình vẽ.
Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.
Lấy điểm A bất kì trên hình màu đỏ sao cho A ≠ O.
Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên hình màu đỏ, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến hình màu đỏ thành chính nó.
⦁ Ta xét hình màu xanh lá:
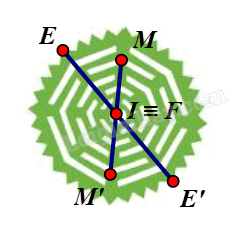
Giả sử ta chọn điểm I trên hình màu xanh lá như hình vẽ.
Lấy điểm F trùng I. Khi đó qua I, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên hình màu xanh lá sao cho E ≠ I.
Khi đó ta luôn xác định được một điểm E’ sao cho I là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác I trên hình màu xanh lá, ta đều xác định được một điểm M’ trên hình sao cho I là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm I biến hình màu xanh lá thành chính nó.
⦁ Ta xét hình màu xanh biển:
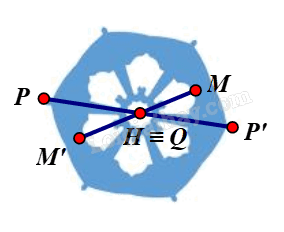
Giả sử ta chọn điểm H trên hình màu xanh biển như hình vẽ.
Lấy điểm P trùng H. Khi đó qua H, điểm đối xứng với P là chính nó.
Lấy điểm P bất kì trên hình màu xanh biển sao cho P ≠ H.
Khi đó ta luôn xác định được một điểm P’ sao cho H là trung điểm của đoạn PP’.
Tương tự như vậy, với mỗi điểm M bất kì khác H trên hình màu xanh biển, ta đều xác định được một điểm M’ trên hình sao cho H là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm H biến hình màu xanh biển thành chính nó.
- Khám phá 1
- Thực hành 1
- Vận dụng 1
Cho điểm O. Gọi f là quy tắc xác định như sau:
a) Với điểm M khác O, xác định điểm M’ sao cho O là trung điểm của MM’ (Hình 1).
b) Với điểm M trùng với O thì f biến điểm M thành chính nó.
Hỏi f có phải là phép biến hình không?

Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
Theo đề, ta có M’ = f(M).
Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
Trong mặt phẳng tọa độ Oxy, cho các điểm I(1; 1), M(2; 2), N(0; –3) và P(–1; –2). Tìm tọa độ các điểm \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right),{\rm{ }}N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right),{\rm{ }}P'{\rm{ }} = {\rm{ }}{Đ_I}\left( P \right).\)
Phương pháp giải:
Nếu thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
+ Ta có \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right).\)
Suy ra I(1; 1) là trung điểm MM’ với M(2; 2).
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M} = 2.1 - 2 = 0\\{y_{M'}} = 2{y_I} - {y_M} = 2.1 - 2 = 0\end{array} \right.\)
Suy ra M’ có tọa độ là (0; 0).
+ Ta có \(N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right).\)
Suy ra I(1; 1) là trung điểm của NN’ với N(0; –3).
Do đó \(\left\{ \begin{array}{l}{x_{N'}} = 2{x_I} - {x_N} = 2.1 - 0 = 2\\{y_{N'}} = 2{y_I} - {y_N} = 2.1 + 3 = 5\end{array} \right.\)
Suy ra N’ có tọa độ là N’(2; 5).
+ Ta có \(P' = {\rm{ }}{Đ_I}\left( P \right).\)
Suy ra I(1; 1) là trung điểm PP’ với P(–1; –2).
Do đó \(\left\{ \begin{array}{l}{x_{P'}} = 2{x_I} - {x_P} = 2.1 + 1 = 3\\{y_{P'}} = 2{y_I} - {y_P} = 2.1 + 2 = 4\end{array} \right.\)
Suy ra P’ có tọa độ là P’(3; 4).
Vậy \(M'\left( {0;{\rm{ }}0} \right),{\rm{ }}N'\left( {2;{\rm{ }}5} \right),{\rm{ }}P'\left( {3;{\rm{ }}4} \right).\)
Tìm phép đối xứng tâm biến mỗi hình sau thành chính nó.

Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
⦁ Ta xét hình màu đỏ:
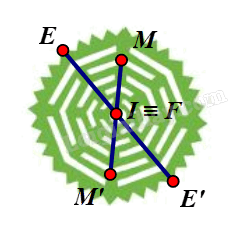
Giả sử ta chọn điểm O trên hình màu đỏ như hình vẽ.
Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.
Lấy điểm A bất kì trên hình màu đỏ sao cho A ≠ O.
Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên hình màu đỏ, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến hình màu đỏ thành chính nó.
⦁ Ta xét hình màu xanh lá:
Giả sử ta chọn điểm I trên hình màu xanh lá như hình vẽ.
Lấy điểm F trùng I. Khi đó qua I, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên hình màu xanh lá sao cho E ≠ I.
Khi đó ta luôn xác định được một điểm E’ sao cho I là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác I trên hình màu xanh lá, ta đều xác định được một điểm M’ trên hình sao cho I là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm I biến hình màu xanh lá thành chính nó.
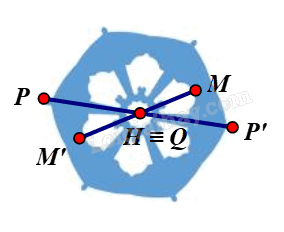
⦁ Ta xét hình màu xanh biển:
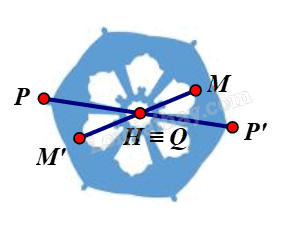
Giả sử ta chọn điểm H trên hình màu xanh biển như hình vẽ.
Lấy điểm P trùng H. Khi đó qua H, điểm đối xứng với P là chính nó.
Lấy điểm P bất kì trên hình màu xanh biển sao cho P ≠ H.
Khi đó ta luôn xác định được một điểm P’ sao cho H là trung điểm của đoạn PP’.
Tương tự như vậy, với mỗi điểm M bất kì khác H trên hình màu xanh biển, ta đều xác định được một điểm M’ trên hình sao cho H là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm H biến hình màu xanh biển thành chính nó.
Giải mục 1 trang 20, 21 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào các kiến thức cơ bản về dãy số, giới hạn dãy số và cấp số. Đây là nền tảng quan trọng để học sinh tiếp cận các kiến thức nâng cao hơn trong chương trình Toán 11. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 1 trang 20, 21, giúp các em học sinh hiểu rõ hơn về các khái niệm và phương pháp giải toán.
Nội dung chính của Mục 1
- Dãy số: Định nghĩa, các loại dãy số (dãy số hữu hạn, dãy số vô hạn, dãy số tăng, dãy số giảm).
- Giới hạn dãy số: Định nghĩa, các tính chất của giới hạn dãy số.
- Cấp số cộng: Định nghĩa, công thức tổng quát, các tính chất.
- Cấp số nhân: Định nghĩa, công thức tổng quát, các tính chất.
Giải chi tiết các bài tập trang 20, 21
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 20, 21 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo:
Bài 1: (Trang 20)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, bao gồm các bước giải, công thức sử dụng và kết luận)
Bài 2: (Trang 20)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, bao gồm các bước giải, công thức sử dụng và kết luận)
Bài 3: (Trang 21)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, bao gồm các bước giải, công thức sử dụng và kết luận)
Mẹo giải toán hiệu quả
Để giải các bài tập về dãy số, giới hạn dãy số và cấp số một cách hiệu quả, các em học sinh cần:
- Nắm vững các định nghĩa, công thức và tính chất cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả sau khi giải xong để đảm bảo tính đúng đắn.
Ứng dụng của kiến thức
Kiến thức về dãy số, giới hạn dãy số và cấp số có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
- Tài chính: Tính lãi kép, tính giá trị tương lai của khoản đầu tư.
- Vật lý: Mô tả các hiện tượng vật lý như dao động, sóng.
- Tin học: Thuật toán, lập trình.
Kết luận
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về dãy số, giới hạn dãy số và cấp số. Chúc các em học tập tốt!
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.