Giải mục 2 trang 72, 73, 74, 75 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 72, 73, 74, 75 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 72, 73, 74, 75 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài giải được các giáo viên có kinh nghiệm biên soạn, đảm bảo tính chính xác và logic.
Chúng tôi luôn cố gắng cung cấp những tài liệu học tập tốt nhất để giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
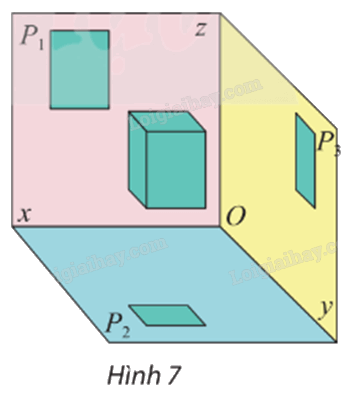
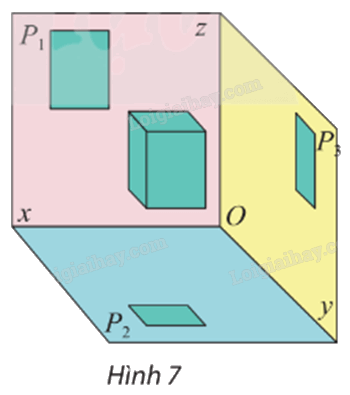
Trong Hình 7, theo em, nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P1), (P2), (P3) có đủ để chế tạo được ℋ không?
Khám phá 2
Trong Hình 7, theo em, nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P1), (P2), (P3) có đủ để chế tạo được ℋ không?
Phương pháp giải:
Quan sát hình 7, suy luận thực tiễn để trả lời.
Lời giải chi tiết:
Ta thấy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P1), (P2), (P3) trong Hình 7 thì hình chiếu đó chỉ thể hiện được một mặt của vật thật dẫn đến chế tạo không chính xác.
Vậy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P1), (P2), (P3) thì không đủ để chế tạo được hình ℋ.
Vận dụng 2
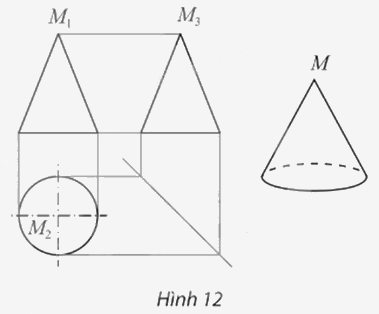
Trong bản vẽ biểu diễn hình nón trong Hình 12.
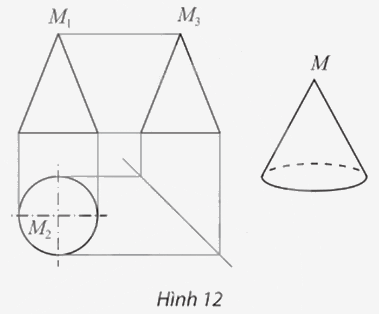
a) Khoảng cách giữa hai đường gióng nào cho ta biết chiều cao của hình nón?
b) Khoảng cách giữa hai đường gióng nào cho ta biết độ dài đường kính đáy của hình nón?
c) Nêu cách xác định điểm M3 biểu diễn đỉnh M của hình nón trong hình chiếu cạnh khi biết hai điểm M1 và M2 biểu diễn M trong hình chiếu đứng và hình chiếu bằng.
Phương pháp giải:
Quan sát hình 12, suy luận để trả lời.
Lời giải chi tiết:
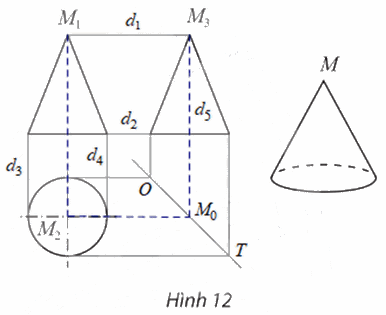
Gọi d1, d2, d3, d4, d5 là các đường gióng của bản vẽ (như hình vẽ).
a) Khoảng cách giữa hai đường gióng d1 và d2 cho ta biết chiều cao của hình nón.
b) Khoảng cách giữa hai đường gióng d3 và d4 cho ta biết độ dài đường kính đáy của hình nón.
c) Gọi OT là đường phân giác của bản vẽ (như hình vẽ).
– Phác họa đường gióng qua M2 và song song với d1, đường gióng này cắt OT tại M0.
– Phác họa đường gióng d5 qua M0 và song song với M1M2.
Giao điểm của d5 và d1 là điểm M3 cần tìm.
Thực hành 2
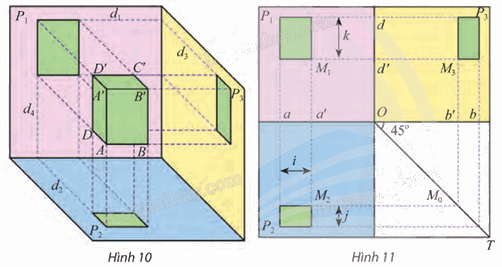
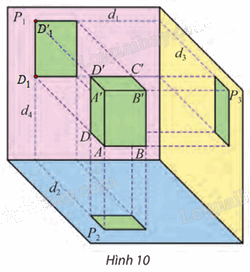
a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên các hình chiếu nào của bản vẽ? Tại sao?
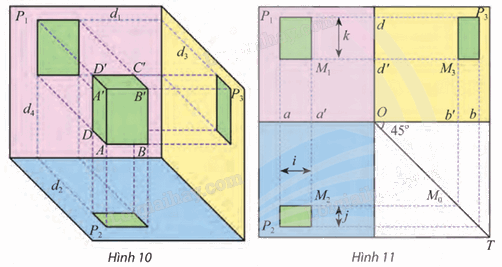
b) Trên Hình 11, tìm hai giao tuyến được biểu diễn thành đường gióng a trên bản vẽ.
c) Trên Hình 11, khoảng cách giữa hai đường gióng nào cho ta chiều cao AA’ của vật ở Hình 10?
Phương pháp giải:
Quan sát hình 10, 11 để trả lời.
Lời giải chi tiết:
a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên hình chiếu bằng và hình chiếu cạnh của bản vẽ vì AD song song với (P2) và (P3).
b) Hai giao tuyến được biểu diễn thành đường gióng a trên Hình 11 là d4 và d2.
c) Trên Hình 11, ta thấy độ dài mũi tên k bằng chiều cao AA’ của vật ở Hình 10.
Vậy trên Hình 11, khoảng cách giữa hai đường gióng d và d’ cho ta chiều cao AA’ của vật ở Hình 10.
Khám phá 3
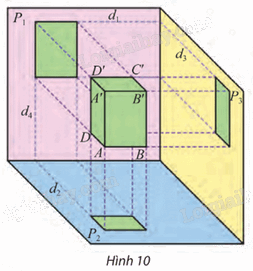
Quan sát Hình 10 và cho biết:
– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật, cạnh nào song song với một trong ba mặt phẳng chiếu (P1), (P2), (P3)?
– Tìm hai giao tuyến của (P1) và (P2) với mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2).
Phương pháp giải:
Quan sát hình 10 để trả lời.
Lời giải chi tiết:
– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật ABCD.A’B’C’D’, ta có:
⦁ Cạnh AB song song với các mặt phẳng chiếu (P1) và (P2);
⦁ Cạnh AA’ song song với các mặt phẳng chiếu (P1) và (P3);
⦁ Cạnh AD song song với các mặt phẳng chiếu (P2) và (P3).
Vậy cả ba cạnh AB, AA’ và AD của hình hộp chữ nhật đều song song với một trong ba mặt phẳng chiếu (P1), (P2) và (P3).
– Xác định hai giao tuyến của (P1) và (P2) với mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2):
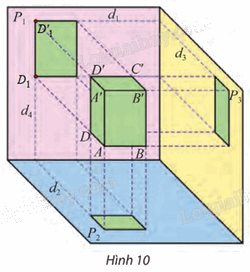
Ta có AD ⊥ AA’ (do ABCD.A’B’C’D’ là hình hộp chữ nhật).
Mà AA’ // (P1).
Suy ra AD ⊥ (P1).
Do đó (AA’D’D) ⊥ (P1).
Chứng minh tương tự, ta được (AA’D’D) ⊥ (P2).
Vì vậy mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2) là (AA’D’D).
Gọi D1, D1’ lần lượt là hình chiếu vuông góc của các điểm D, D’ lên mặt phẳng (P1).
Suy ra D1, D1’∈ (AA’D’D) và D1, D1’∈ (P1).
Do đó hay d4 = (AA’D’D) ∩ (P1).
Chứng minh tương tự, ta được d2 = (AA’D’D) ∩ (P2).
Vậy d4, d2 lần lượt là hai giao tuyến cần tìm.
- Khám phá 2
- Khám phá 3
- Thực hành 2
- Vận dụng 2
Trong Hình 7, theo em, nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P1), (P2), (P3) có đủ để chế tạo được ℋ không?
Phương pháp giải:
Quan sát hình 7, suy luận thực tiễn để trả lời.
Lời giải chi tiết:
Ta thấy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P1), (P2), (P3) trong Hình 7 thì hình chiếu đó chỉ thể hiện được một mặt của vật thật dẫn đến chế tạo không chính xác.
Vậy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P1), (P2), (P3) thì không đủ để chế tạo được hình ℋ.
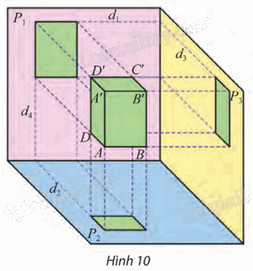
Quan sát Hình 10 và cho biết:
– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật, cạnh nào song song với một trong ba mặt phẳng chiếu (P1), (P2), (P3)?
– Tìm hai giao tuyến của (P1) và (P2) với mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2).
Phương pháp giải:
Quan sát hình 10 để trả lời.
Lời giải chi tiết:
– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật ABCD.A’B’C’D’, ta có:
⦁ Cạnh AB song song với các mặt phẳng chiếu (P1) và (P2);
⦁ Cạnh AA’ song song với các mặt phẳng chiếu (P1) và (P3);
⦁ Cạnh AD song song với các mặt phẳng chiếu (P2) và (P3).
Vậy cả ba cạnh AB, AA’ và AD của hình hộp chữ nhật đều song song với một trong ba mặt phẳng chiếu (P1), (P2) và (P3).
– Xác định hai giao tuyến của (P1) và (P2) với mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2):
Ta có AD ⊥ AA’ (do ABCD.A’B’C’D’ là hình hộp chữ nhật).
Mà AA’ // (P1).
Suy ra AD ⊥ (P1).
Do đó (AA’D’D) ⊥ (P1).
Chứng minh tương tự, ta được (AA’D’D) ⊥ (P2).
Vì vậy mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2) là (AA’D’D).
Gọi D1, D1’ lần lượt là hình chiếu vuông góc của các điểm D, D’ lên mặt phẳng (P1).
Suy ra D1, D1’∈ (AA’D’D) và D1, D1’∈ (P1).
Do đó hay d4 = (AA’D’D) ∩ (P1).
Chứng minh tương tự, ta được d2 = (AA’D’D) ∩ (P2).
Vậy d4, d2 lần lượt là hai giao tuyến cần tìm.
a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên các hình chiếu nào của bản vẽ? Tại sao?
b) Trên Hình 11, tìm hai giao tuyến được biểu diễn thành đường gióng a trên bản vẽ.
c) Trên Hình 11, khoảng cách giữa hai đường gióng nào cho ta chiều cao AA’ của vật ở Hình 10?
Phương pháp giải:
Quan sát hình 10, 11 để trả lời.
Lời giải chi tiết:
a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên hình chiếu bằng và hình chiếu cạnh của bản vẽ vì AD song song với (P2) và (P3).
b) Hai giao tuyến được biểu diễn thành đường gióng a trên Hình 11 là d4 và d2.
c) Trên Hình 11, ta thấy độ dài mũi tên k bằng chiều cao AA’ của vật ở Hình 10.
Vậy trên Hình 11, khoảng cách giữa hai đường gióng d và d’ cho ta chiều cao AA’ của vật ở Hình 10.
Trong bản vẽ biểu diễn hình nón trong Hình 12.
a) Khoảng cách giữa hai đường gióng nào cho ta biết chiều cao của hình nón?
b) Khoảng cách giữa hai đường gióng nào cho ta biết độ dài đường kính đáy của hình nón?
c) Nêu cách xác định điểm M3 biểu diễn đỉnh M của hình nón trong hình chiếu cạnh khi biết hai điểm M1 và M2 biểu diễn M trong hình chiếu đứng và hình chiếu bằng.
Phương pháp giải:
Quan sát hình 12, suy luận để trả lời.
Lời giải chi tiết:
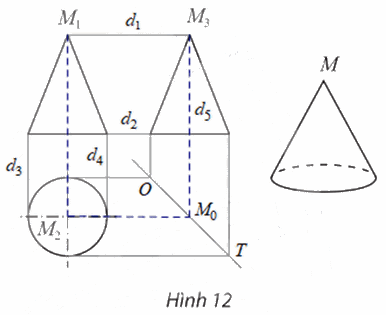
Gọi d1, d2, d3, d4, d5 là các đường gióng của bản vẽ (như hình vẽ).
a) Khoảng cách giữa hai đường gióng d1 và d2 cho ta biết chiều cao của hình nón.
b) Khoảng cách giữa hai đường gióng d3 và d4 cho ta biết độ dài đường kính đáy của hình nón.
c) Gọi OT là đường phân giác của bản vẽ (như hình vẽ).
– Phác họa đường gióng qua M2 và song song với d1, đường gióng này cắt OT tại M0.
– Phác họa đường gióng d5 qua M0 và song song với M1M2.
Giao điểm của d5 và d1 là điểm M3 cần tìm.
Giải mục 2 trang 72, 73, 74, 75 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng vào giải bài tập. Việc giải các bài tập trong mục này không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng quan trọng trong học tập và cuộc sống.
Nội dung chính của Mục 2 (trang 72, 73, 74, 75)
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định chính xác nội dung mà nó bao gồm. Thông thường, các bài tập trong mục này sẽ xoay quanh các khái niệm và định lý sau (tùy thuộc vào chương cụ thể):
- Khái niệm về giới hạn của hàm số: Định nghĩa, các tính chất cơ bản.
- Giới hạn một bên: Giới hạn trái, giới hạn phải.
- Các dạng giới hạn vô cùng: Giới hạn khi x tiến tới vô cùng, giới hạn khi x tiến tới một số.
- Ứng dụng của giới hạn: Tính giới hạn của hàm số, xét tính liên tục của hàm số.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 72, 73, 74, 75:
Bài tập 1: Tính giới hạn limx→2 (x2 - 4) / (x - 2)
Giải:
- Phân tích tử thức: x2 - 4 = (x - 2)(x + 2)
- Rút gọn biểu thức: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
- Tính giới hạn: limx→2 (x + 2) = 2 + 2 = 4
Vậy, limx→2 (x2 - 4) / (x - 2) = 4
Bài tập 2: Tính giới hạn limx→+∞ (2x + 1) / (x - 3)
Giải:
Chia cả tử và mẫu cho x:
limx→+∞ (2x + 1) / (x - 3) = limx→+∞ (2 + 1/x) / (1 - 3/x)
Vì limx→+∞ 1/x = 0 và limx→+∞ 3/x = 0, nên:
limx→+∞ (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2
Vậy, limx→+∞ (2x + 1) / (x - 3) = 2
Mẹo giải bài tập giới hạn
- Sử dụng các công thức giới hạn cơ bản.
- Biến đổi biểu thức để đưa về dạng có thể tính giới hạn được.
- Áp dụng quy tắc L'Hopital khi gặp dạng vô định.
- Kiểm tra lại kết quả sau khi giải.
Tầm quan trọng của việc nắm vững kiến thức về giới hạn
Kiến thức về giới hạn là nền tảng quan trọng cho việc học các khái niệm nâng cao hơn trong Toán học, như đạo hàm, tích phân và giải tích. Việc nắm vững kiến thức này sẽ giúp học sinh giải quyết các bài toán phức tạp một cách dễ dàng và hiệu quả hơn.
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Mục 2 trang 72, 73, 74, 75 Chuyên đề học tập Toán 11 - Chân trời sáng tạo và đạt kết quả tốt trong môn học.