Giải mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 11 của Chuyên đề học tập Toán 11, bộ sách Chân trời sáng tạo.
Chúng tôi sẽ giúp bạn hiểu rõ các khái niệm, công thức và phương pháp giải bài tập, từ đó nâng cao kết quả học tập môn Toán.
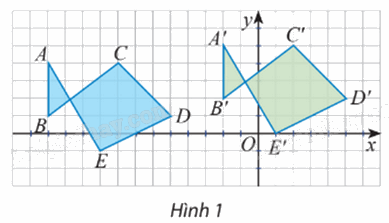
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).
Thực hành 1
Chứng minh phép đồng nhất là một phép tịnh tiến.
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
Giả sử A’ là ảnh của A qua phép đồng nhất f. Tức là, A’ = f(A).
Suy ra \(A'{\rm{ }} \equiv {\rm{ }}A\) hay \(AA'{\rm{ }} = {\rm{ }}0.\)
Khi đó \(\overrightarrow {AA'} = \vec 0\).
Tương tự như vậy, với mỗi điểm M bất kì, ta lấy điểm M’ là ảnh của điểm M qua phép đồng nhất f.
Khi đó ta cũng có \(\overrightarrow {MM'} = \vec 0\).
Vậy phép đồng nhất là một phép tịnh tiến theo \(\vec 0\)
Khám phá 1
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).
a) Có nhận xét gì về các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \)
b) Có hay không phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’?
Phương pháp giải:
Quan sát hình 1, nhận xét về hướng, độ dài của các vectơ
Lời giải chi tiết:
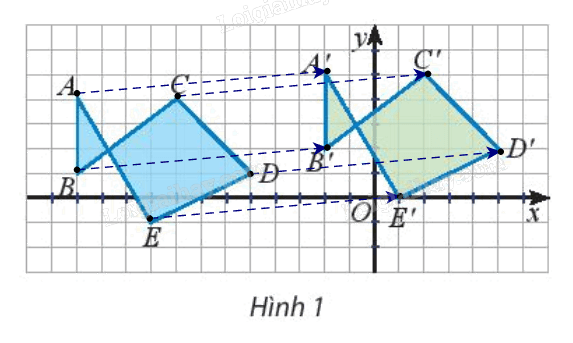
a) Quan sát Hình 1, ta thấy các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \) cùng hướng và có độ dài bằng nhau.
Vậy \(\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
b) Ta đặt \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
Khi đó tồn tại phép biến hình biến điểm A thành điểm A’ sao cho \(\overrightarrow {AA'} = {\rm{\vec u}}\)
Tương tự như vậy, ta thấy phép biến hình đó cũng biến các điểm B, C, D, E thành các điểm B’, C’, D’, E’ sao cho \(\overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} = {\rm{\vec u}}\)
Vậy có phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’
Vận dụng 1
Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị).
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Lời giải chi tiết:
Từ Hoạt động khám phá 1, ta có \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \).
Ta đặt \({\rm{\vec v}} = {\rm{\vec u}}\)
Khi đó phép tịnh tiến theo \({\rm{\vec v}} = {\rm{\vec u}}\) biến các điểm A, B, C, D, E thành điểm A’, B’, C’, D’, E’.
Dựng \(\Delta AA'M\) vuông tại M (như hình vẽ).
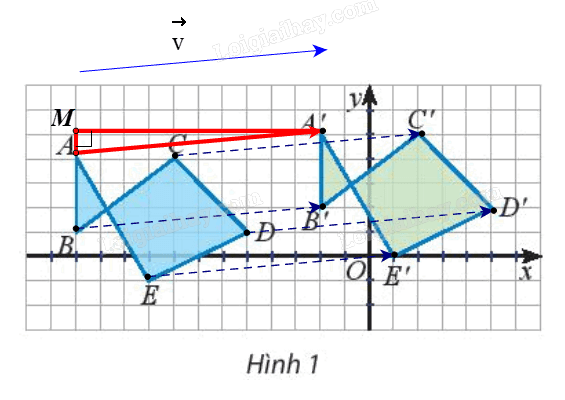
Ta có \(AM{\rm{ }} = {\rm{ }}1\) (đơn vị), \(A'M{\rm{ }} = {\rm{ }}10\) (đơn vị) (do cạnh mỗi ô vuông là 1 đơn vị).
Suy ra \(AA' = \sqrt {A{M^2} + {\rm{A'}}{{\rm{M}}^2}} = \sqrt {{1^2} + {{10}^2}} = \sqrt {101} \).
Khi đó \(\left| {{\rm{\vec v}}} \right| = \left| {\overrightarrow {AA'} } \right| = AA' = \sqrt {101} \)
Vậy độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) là \(\sqrt {101} \).
- Khám phá 1
- Thực hành 1
- Vận dụng 1
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).
a) Có nhận xét gì về các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \)
b) Có hay không phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’?
Phương pháp giải:
Quan sát hình 1, nhận xét về hướng, độ dài của các vectơ
Lời giải chi tiết:
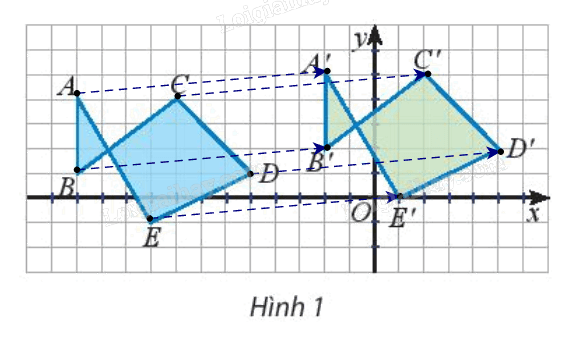
a) Quan sát Hình 1, ta thấy các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \) cùng hướng và có độ dài bằng nhau.
Vậy \(\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
b) Ta đặt \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
Khi đó tồn tại phép biến hình biến điểm A thành điểm A’ sao cho \(\overrightarrow {AA'} = {\rm{\vec u}}\)
Tương tự như vậy, ta thấy phép biến hình đó cũng biến các điểm B, C, D, E thành các điểm B’, C’, D’, E’ sao cho \(\overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} = {\rm{\vec u}}\)
Vậy có phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’
Chứng minh phép đồng nhất là một phép tịnh tiến.
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
Giả sử A’ là ảnh của A qua phép đồng nhất f. Tức là, A’ = f(A).
Suy ra \(A'{\rm{ }} \equiv {\rm{ }}A\) hay \(AA'{\rm{ }} = {\rm{ }}0.\)
Khi đó \(\overrightarrow {AA'} = \vec 0\).
Tương tự như vậy, với mỗi điểm M bất kì, ta lấy điểm M’ là ảnh của điểm M qua phép đồng nhất f.
Khi đó ta cũng có \(\overrightarrow {MM'} = \vec 0\).
Vậy phép đồng nhất là một phép tịnh tiến theo \(\vec 0\)
Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị).
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Lời giải chi tiết:
Từ Hoạt động khám phá 1, ta có \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \).
Ta đặt \({\rm{\vec v}} = {\rm{\vec u}}\)
Khi đó phép tịnh tiến theo \({\rm{\vec v}} = {\rm{\vec u}}\) biến các điểm A, B, C, D, E thành điểm A’, B’, C’, D’, E’.
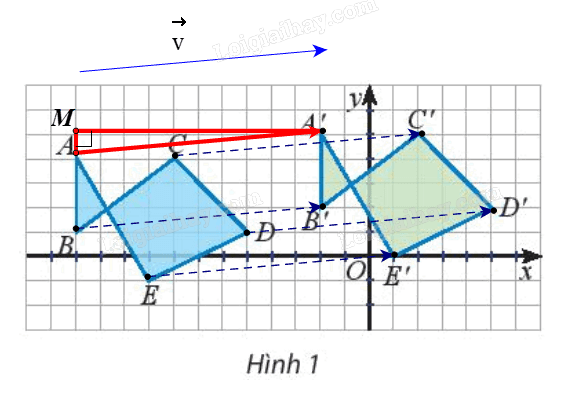
Dựng \(\Delta AA'M\) vuông tại M (như hình vẽ).
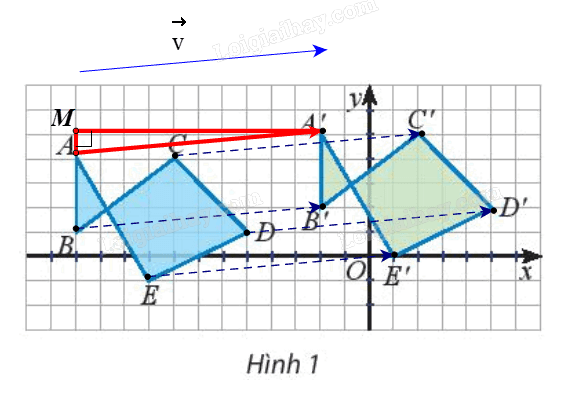
Ta có \(AM{\rm{ }} = {\rm{ }}1\) (đơn vị), \(A'M{\rm{ }} = {\rm{ }}10\) (đơn vị) (do cạnh mỗi ô vuông là 1 đơn vị).
Suy ra \(AA' = \sqrt {A{M^2} + {\rm{A'}}{{\rm{M}}^2}} = \sqrt {{1^2} + {{10}^2}} = \sqrt {101} \).
Khi đó \(\left| {{\rm{\vec v}}} \right| = \left| {\overrightarrow {AA'} } \right| = AA' = \sqrt {101} \)
Vậy độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) là \(\sqrt {101} \).
Giải mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 1 trang 11 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào việc ôn tập và củng cố kiến thức về một chủ đề cụ thể. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức liên quan và phương pháp giải bài tập phù hợp.
Nội dung chính của Mục 1 trang 11
Thông thường, Mục 1 trang 11 sẽ bao gồm các dạng bài tập sau:
- Bài tập trắc nghiệm: Kiểm tra khả năng hiểu và vận dụng kiến thức cơ bản.
- Bài tập tự luận: Yêu cầu học sinh trình bày lời giải chi tiết, thể hiện khả năng phân tích và suy luận logic.
- Bài tập ứng dụng: Liên hệ kiến thức toán học với các tình huống thực tế.
Lời giải chi tiết các bài tập
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1 trang 11:
Bài 1: (Ví dụ minh họa)
Đề bài: Giải phương trình: 2x + 5 = 11
Lời giải:
- Chuyển 5 sang vế phải: 2x = 11 - 5
- Rút gọn: 2x = 6
- Chia cả hai vế cho 2: x = 3
Kết luận: Phương trình có nghiệm x = 3.
Bài 2: (Ví dụ minh họa)
Đề bài: Tính giá trị của biểu thức: A = (x + 2)(x - 2)
Lời giải:
Sử dụng hằng đẳng thức (a + b)(a - b) = a2 - b2, ta có:
A = x2 - 4
Kết luận: Giá trị của biểu thức A là x2 - 4.
Mẹo giải bài tập hiệu quả
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài tập.
- Xác định kiến thức cần sử dụng: Liên hệ bài tập với các khái niệm, công thức đã học.
- Lập kế hoạch giải bài: Xác định các bước cần thực hiện để giải bài tập.
- Kiểm tra lại lời giải: Đảm bảo tính chính xác và hợp lý của lời giải.
Tài liệu tham khảo hữu ích
Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 - Chân trời sáng tạo
- Sách bài tập Toán 11 - Chân trời sáng tạo
- Các trang web học Toán trực tuyến uy tín (ví dụ: tusach.vn)
Kết luận
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết các bài tập trong Mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc bạn học tập tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | Xem chi tiết ở trên |
| Bài 2 | Xem chi tiết ở trên |
| Đây chỉ là ví dụ minh họa, hãy tham khảo lời giải chi tiết cho từng bài tập cụ thể. | |