Giải mục 3 trang 22, 23 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 22, 23 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 22, 23 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho các em.
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.
Vận dụng 3
Trong Hình 10, hình nào có tâm đối xứng? (Mỗi chữ cái là một hình).

Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
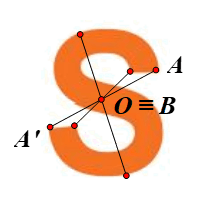
⦁ Giả sử O là một điểm trên hình chữ S (hình vẽ).
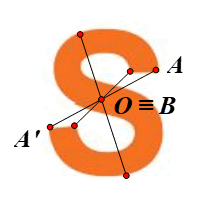
Lấy điểm A bất kì trên hình chữ S sao cho \(A{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm A’ trên hình chữ S sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right).\)
Lấy điểm B trùng O. Khi đó
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình chữ S, ta đều xác định được ảnh của các điểm đó qua ĐO trên hình chữ S.
Vì vậy O là tâm đối xứng của hình chữ S.
⦁ Giả sử O là một điểm trên hình chữ H (hình vẽ).
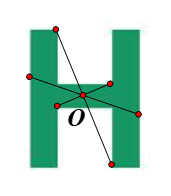
Chứng minh tương tự như trên, ta được O là tâm đối xứng của hình chữ H.
⦁ Các hình còn lại không có tâm đối xứng.
Vậy hình chữ S và hình chữ H có tâm đối xứng là điểm O như hình vẽ.
Khám phá 3
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.
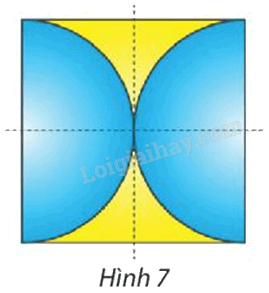
Phương pháp giải:
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục qua d biến H thành chính nó.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
⦁ Giả sử ta chọn đường thẳng d trên Hình 7 như hình vẽ.
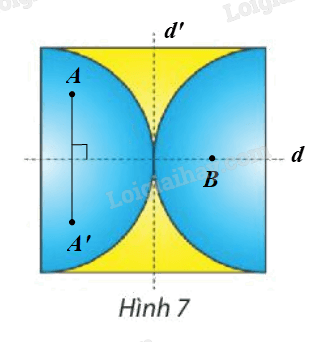
Lấy điểm A nằm trên Hình 7 nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên Hình 7 ban đầu.
Lấy điểm B nằm trên Hình 7 và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì trên Hình 7, ta đều xác định được ảnh của các điểm đó qua \({Đ_d}\) trên Hình 7.
Vậy phép đối xứng trục d biến Hình 7 thành chính nó.
Giả sử ta chọn đường thẳng d’ trên Hình 7 như hình vẽ.
Chứng minh tương tự như trên, ta cũng xác định được phép đối xứng trục d’ biến Hình 7 thành chính nó.
⦁ Giả sử ta chọn điểm O trên Hình 7 như hình vẽ.
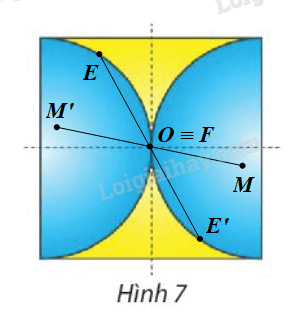
Lấy điểm F trùng O. Khi đó qua O, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên Hình 7 sao cho \(E{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm E’ trên Hình 7 sao cho O là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên Hình 7, ta đều xác định được một điểm M’ trên Hình 7 sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến Hình 7 thành chính nó.
Thực hành 3
a) Trong Hình 9, hình nào có tâm đối xứng? Tìm tâm đối xứng (nếu có).
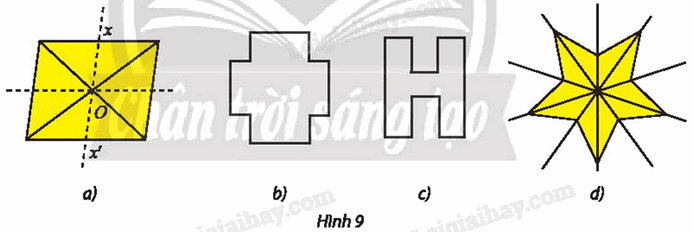
b) Nêu tên một hình có vô số tâm đối xứng.
Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
a) ⦁ Hình 9a:
Ta đặt hình bình hành ở Hình 9a có các đỉnh là A, B, C, D (hình vẽ).
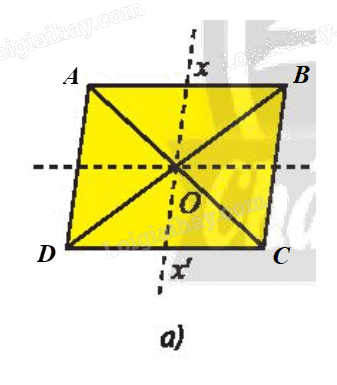
Hình bình hành ABCD có tâm O là giao điểm hai đường chéo.
Suy ra O là trung điểm của AC, do đó \(C{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right),A{\rm{ }} = {\rm{ }}{Đ_O}\left( C \right).\)
Chứng minh tương tự, ta được \(B{\rm{ }} = {\rm{ }}{Đ_O}\left( D \right),D{\rm{ }} = {\rm{ }}{Đ_O}\left( B \right).\)
Do đó ảnh của hình bình hành ABCD qua \({Đ_O}\) là chính nó.
Vậy O là tâm đối xứng của Hình 9a.
⦁ Hình 9b:

Giả sử I là một điểm trên Hình 9b (hình vẽ).
Lấy điểm A bất kì trên Hình 9b sao cho \(A{\rm{ }} \ne {\rm{ }}I.\)
Khi đó ta luôn xác định được một điểm A’ trên Hình 9b sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_I}\left( A \right).\)
Lấy điểm B trùng I. Khi đó \(B{\rm{ }} = {\rm{ }}{Đ_I}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì nằm trên Hình 9b, ta đều xác định được ảnh của các điểm đó qua ĐI trên Hình 9b.
Vậy I là tâm đối xứng của Hình 9b.
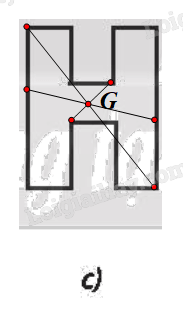
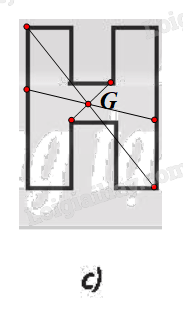
⦁ Hình 9c:
Chứng minh tương tự Hình 9b, ta được G là tâm đối xứng của Hình 9c.
⦁ Hình 9d không có tâm đối xứng.
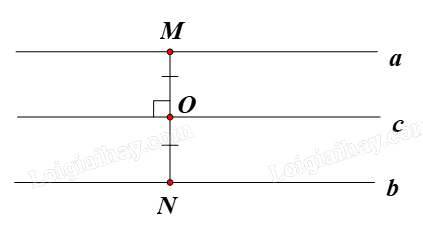
b) Hình có vô số tâm đối xứng là:
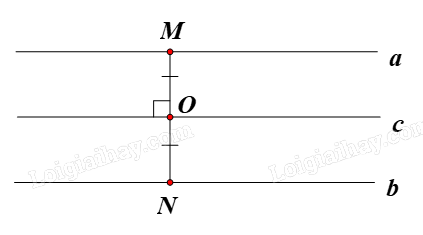
– Đường thẳng: do đường thẳng không có điểm đầu và điểm cuối nên mỗi điểm bất kì nằm trên đường thẳng đều là tâm đối xứng của đường thẳng đó;
– Hình gồm hai đường thẳng song song: tâm đối xứng của hình gồm hai đường thẳng song song luôn di động trên một đường thẳng cố định, đường thẳng đó là trục đối xứng của hai đường thẳng đã cho.
Cụ thể, giả sử O là tâm đối xứng của hai đường thẳng song song a và b. Khi đó O di động trên đường thẳng c là trục đối xứng của hai đường thẳng a và b.
- Khám phá 3
- Thực hành 3
- Vận dụng 3
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.

Phương pháp giải:
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục qua d biến H thành chính nó.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
⦁ Giả sử ta chọn đường thẳng d trên Hình 7 như hình vẽ.
Lấy điểm A nằm trên Hình 7 nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên Hình 7 ban đầu.
Lấy điểm B nằm trên Hình 7 và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì trên Hình 7, ta đều xác định được ảnh của các điểm đó qua \({Đ_d}\) trên Hình 7.
Vậy phép đối xứng trục d biến Hình 7 thành chính nó.
Giả sử ta chọn đường thẳng d’ trên Hình 7 như hình vẽ.
Chứng minh tương tự như trên, ta cũng xác định được phép đối xứng trục d’ biến Hình 7 thành chính nó.
⦁ Giả sử ta chọn điểm O trên Hình 7 như hình vẽ.
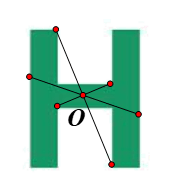
Lấy điểm F trùng O. Khi đó qua O, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên Hình 7 sao cho \(E{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm E’ trên Hình 7 sao cho O là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên Hình 7, ta đều xác định được một điểm M’ trên Hình 7 sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến Hình 7 thành chính nó.
a) Trong Hình 9, hình nào có tâm đối xứng? Tìm tâm đối xứng (nếu có).
b) Nêu tên một hình có vô số tâm đối xứng.
Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
a) ⦁ Hình 9a:
Ta đặt hình bình hành ở Hình 9a có các đỉnh là A, B, C, D (hình vẽ).
Hình bình hành ABCD có tâm O là giao điểm hai đường chéo.
Suy ra O là trung điểm của AC, do đó \(C{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right),A{\rm{ }} = {\rm{ }}{Đ_O}\left( C \right).\)
Chứng minh tương tự, ta được \(B{\rm{ }} = {\rm{ }}{Đ_O}\left( D \right),D{\rm{ }} = {\rm{ }}{Đ_O}\left( B \right).\)
Do đó ảnh của hình bình hành ABCD qua \({Đ_O}\) là chính nó.
Vậy O là tâm đối xứng của Hình 9a.
⦁ Hình 9b:

Giả sử I là một điểm trên Hình 9b (hình vẽ).
Lấy điểm A bất kì trên Hình 9b sao cho \(A{\rm{ }} \ne {\rm{ }}I.\)
Khi đó ta luôn xác định được một điểm A’ trên Hình 9b sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_I}\left( A \right).\)
Lấy điểm B trùng I. Khi đó \(B{\rm{ }} = {\rm{ }}{Đ_I}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì nằm trên Hình 9b, ta đều xác định được ảnh của các điểm đó qua ĐI trên Hình 9b.
Vậy I là tâm đối xứng của Hình 9b.
⦁ Hình 9c:
Chứng minh tương tự Hình 9b, ta được G là tâm đối xứng của Hình 9c.
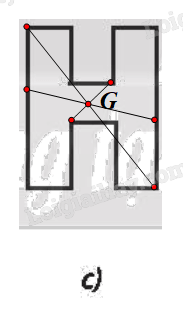
⦁ Hình 9d không có tâm đối xứng.
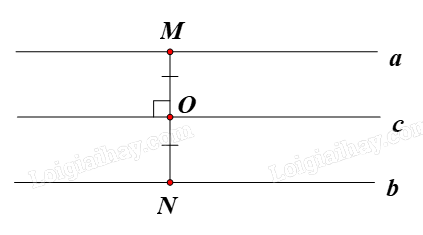
b) Hình có vô số tâm đối xứng là:
– Đường thẳng: do đường thẳng không có điểm đầu và điểm cuối nên mỗi điểm bất kì nằm trên đường thẳng đều là tâm đối xứng của đường thẳng đó;
– Hình gồm hai đường thẳng song song: tâm đối xứng của hình gồm hai đường thẳng song song luôn di động trên một đường thẳng cố định, đường thẳng đó là trục đối xứng của hai đường thẳng đã cho.
Cụ thể, giả sử O là tâm đối xứng của hai đường thẳng song song a và b. Khi đó O di động trên đường thẳng c là trục đối xứng của hai đường thẳng a và b.
Trong Hình 10, hình nào có tâm đối xứng? (Mỗi chữ cái là một hình).

Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
⦁ Giả sử O là một điểm trên hình chữ S (hình vẽ).
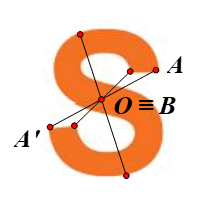
Lấy điểm A bất kì trên hình chữ S sao cho \(A{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm A’ trên hình chữ S sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right).\)
Lấy điểm B trùng O. Khi đó
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình chữ S, ta đều xác định được ảnh của các điểm đó qua ĐO trên hình chữ S.
Vì vậy O là tâm đối xứng của hình chữ S.
⦁ Giả sử O là một điểm trên hình chữ H (hình vẽ).
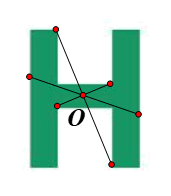
Chứng minh tương tự như trên, ta được O là tâm đối xứng của hình chữ H.
⦁ Các hình còn lại không có tâm đối xứng.
Vậy hình chữ S và hình chữ H có tâm đối xứng là điểm O như hình vẽ.
Giải mục 3 trang 22, 23 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trang 22, 23 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức quan trọng. Tusach.vn sẽ cung cấp một hướng dẫn chi tiết, từng bước giải quyết từng bài tập, giúp các em hiểu rõ phương pháp và cách tiếp cận vấn đề.
Nội dung chính của Mục 3 trang 22, 23
Thông thường, mục này sẽ bao gồm các dạng bài tập sau:
- Bài tập áp dụng định nghĩa: Kiểm tra sự hiểu biết cơ bản về các khái niệm đã học.
- Bài tập vận dụng định lý: Sử dụng các định lý để chứng minh hoặc tính toán.
- Bài tập kết hợp kiến thức: Yêu cầu học sinh kết hợp nhiều kiến thức khác nhau để giải quyết vấn đề.
- Bài tập nâng cao: Thách thức khả năng tư duy và sáng tạo của học sinh.
Lời giải chi tiết từng bài tập
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3 trang 22, 23:
Bài 1: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài là tính giá trị của biểu thức A = sin230° + cos230°)
Lời giải:
- Áp dụng công thức lượng giác cơ bản: sin2α + cos2α = 1
- Thay α = 30° vào công thức: sin230° + cos230° = 1
- Vậy, A = 1
Bài 2: (Ví dụ minh họa)
Đề bài: (Giả sử đề bài là chứng minh đẳng thức: tan x * cos x = sin x)
Lời giải:
Ta có: tan x = sin x / cos x
Do đó: tan x * cos x = (sin x / cos x) * cos x = sin x
Vậy, đẳng thức được chứng minh.
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong mục này một cách nhanh chóng và hiệu quả, các em có thể áp dụng một số mẹo sau:
- Nắm vững các công thức lượng giác: Các công thức lượng giác là công cụ quan trọng để giải quyết các bài tập liên quan đến hàm số lượng giác.
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp các em tính toán nhanh chóng và chính xác các giá trị lượng giác.
- Vẽ hình minh họa: Vẽ hình minh họa có thể giúp các em hình dung rõ hơn về bài toán và tìm ra phương pháp giải quyết phù hợp.
- Luyện tập thường xuyên: Luyện tập thường xuyên là cách tốt nhất để nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Tài liệu tham khảo thêm
Ngoài sách giáo khoa và chuyên đề học tập, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11: Cung cấp nhiều bài tập đa dạng và phong phú để các em luyện tập.
- Các trang web học Toán trực tuyến: Cung cấp các bài giảng, bài tập và lời giải chi tiết.
- Các video hướng dẫn giải Toán: Giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập.
Tusach.vn hy vọng rằng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải quyết các bài tập trong mục 3 trang 22, 23 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!