Lựa chọn câu để xem lời giải nhanh hơn- Hoạt động 3
- Luyện tập 3
- Vận dụng 2
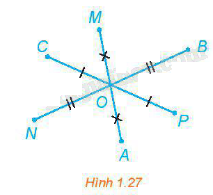
Trong hình 1.27, hãy chỉ ra ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \).
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
Ảnh của các điểm A, B, C, M, N, P qua phép quay tâm O, quay quay \(\pi \) lần lượt là M, N, P, A, B, C.
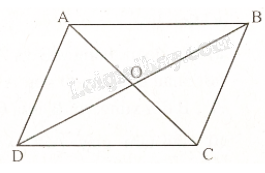
Cho hình hình hành ABCD có hai đường chéo cắt nhau tại O. Tìm ảnh của đường thẳng AB qua \(Đ_{O}\)
Phương pháp giải:
- Tìm ảnh của từng điểm A, B qua . Sau đó nối chúng với nhau ta được ảnh của AB qua \(Đ_{O}\)
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \(Đ_{O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
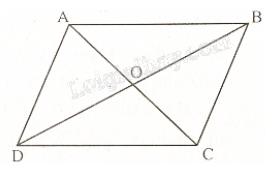
Vì ABCD là hình bình hành nên AC cắt BD tại O với O là trung điểm của AC và BD.
Do đó, C là ảnh của A qua phép đối xứng tâm O; D là ảnh của B qua phép đối xứng tâm O.
Vậy CD là ảnh của AB qua phép đối xứng tâm O.
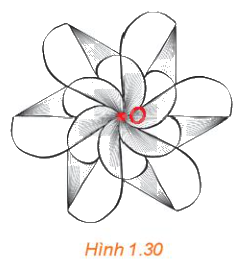
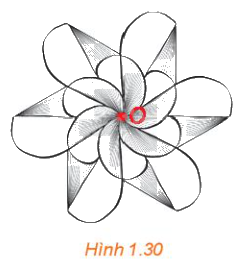
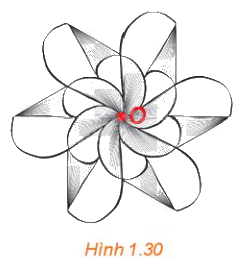
Quan sát Hình 1.30, những phát biểu nào trong các phát biểu sau là đúng?
a) Hình vẽ nhận điểm O (được tô đỏ) làm tâm đối xứng.
b) Một đường thẳng bất kì đi qua điểm O sẽ chia hình vẽ thành hai nửa A và B giống nhau. Nếu thực hiện phép quay tâm O, góc quay 180∘ thì nửa A biến thành nửa B, tức là, B là ảnh của A qua một phép đối xứng tâm O.
c) Có thể chia hình vẽ thành bốn phần giống nhau.
Phương pháp giải:
Quan sát hình 1.30 và dựa vào kiến thức: Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
Phát biểu a, b, c đều đúng.