Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0\) và hai điểm \(A\left( {-{\rm{ }}1;{\rm{ }}2} \right),{\rm{ }}B\left( {-{\rm{ }}3;{\rm{ }}4} \right).\)
a) Tìm tọa độ điểm \(A'\) là ảnh của điểm A qua phép đối xứng trục \(\Delta \)
b) Xác định điểm M thuộc đường thẳng \(\Delta \) sao cho MA + MB đạt giá trị nhỏ nhất.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đã học về phép đối xứng trục để làm
Lời giải chi tiết
a) Ta có: \(2{\rm{ }}.{\rm{ }}\left( {-{\rm{ }}1} \right){\rm{ }}-{\rm{ }}2{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}-{\rm{ }}5{\rm{ }} \ne {\rm{ }}0\) nên \(A\left( {-{\rm{ }}1;{\rm{ }}2} \right)\) không thuộc ∆.
Gọi H là chân đường vuông góc hạ từ A xuống ∆.
Vì H thuộc ∆ nên \(H\left( {x;2x-1} \right)\). Ta có: \(\overrightarrow {AH} = (x + 1;2x - 3)\), vectơ chỉ phương của đường thẳng ∆ là \(\overrightarrow {{u_\Delta }} = \left( {1;\,2} \right)\)
Vì AH vuông góc với ∆ nên \(\overrightarrow {AH} .\overrightarrow {{u_\Delta }} = 0 \Leftrightarrow \left( {x + 1} \right).1 + \left( {2x - 3} \right).2 = 0 \Rightarrow x = 1\)
Từ đó suy ra H(1; 1).
Vì A' là ảnh của điểm A qua phép đối xứng trục ∆ nên AA' vuông góc với ∆ tại H và H là trung điểm của AA'.
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 2{x_H} - {x_A} = 2.1 - \left( { - 1} \right) = 3}\\{{y_{A'}} = 2{y_H} - {y_A} = 2.1 - 2 = 0}\end{array}} \right.\)
Vậy A'(3; 0).
b)
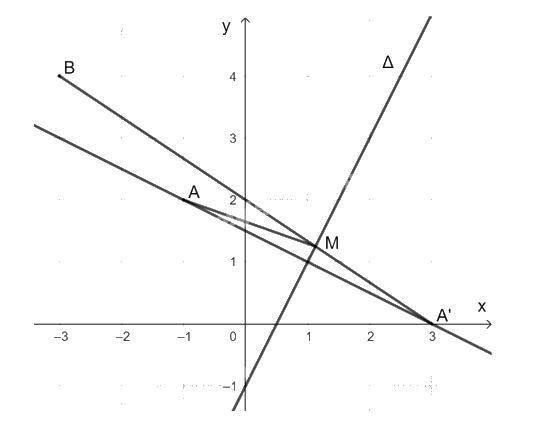
Ta có: \(2.\left( {-3} \right)-4-1{\rm{ }} = -11;{\rm{ 2}}.\left( {-1} \right)-2-1 = -5\) và \(\left( {-11} \right).\left( {-5} \right) = 55 > 0\)nên hai điểm A và B nằm về một phía của đường thẳng ∆.
Vì M thuộc \(\Delta \) và A và A' đối xứng nhau qua \(\Delta \) nên MA = MA' và A' và B nằm về hai phía của đường thẳng \(\Delta \).
Do đó, MA + MB = MA' + MB đạt giá trị nhỏ nhất khi M là giao điểm của A'B và \(\Delta \).
Ta có: \(\overrightarrow {A'B} = ( - 6;4)\), suy ra \(\overrightarrow {{n_{A'B}}} = (2;3)\) là một vectơ pháp tuyến của đường thẳng A'B. Phương trình đường thẳng A'B là \(2\left( {x-3} \right) + 3\left( {y-0} \right) = 0\) hay \(2x + 3y-6 = 0.\)
Tọa độ giao điểm M của A'B và ∆ là nghiệm của hệ phương trình
\(\left\{ {\begin{array}{*{20}{l}}{2x - y - 1 = 0}\\{2x + 3y - 6 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{9}{8}}\\{y = \frac{5}{4}}\end{array}} \right.} \right.\)
Vậy \(M\left( {\frac{9}{8};\,\frac{5}{4}} \right)\).

