Logo

Giải bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức

Tổng quan nội dung

Giải bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

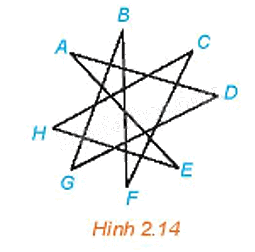
Cho đồ thị G như Hình 2.14.

Đề bài

Cho đồ thị G như Hình 2.14.

a) Tìm một đường đi từ đỉnh A đến đỉnh B.

b) G có liên thông không?

c) Trong G có chu trình sơ cấp nào không?

Giải bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Phương pháp giải - Xem chi tiếtGiải bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức 2

Một đồ thị được gọi là liên thông nếu hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.

Lời giải chi tiết

a) Một đường đi từ đỉnh A đến đỉnh B là: ADGB.

b) Ta thấy hai đỉnh bất kì của đồ thị đều liên thông (tức là đều có đường đi nối chúng), nên G liên thông.

c) Chu trình sơ cấp trong G là: AEHCFBGDA.

Giải bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu

Bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:

  1. Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần khảo sát.
  2. Tìm tập xác định của hàm số: Xác định miền giá trị mà hàm số có thể nhận.
  3. Tính đạo hàm cấp nhất: Tính đạo hàm f'(x) của hàm số.
  4. Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm dừng của hàm số.
  5. Khảo sát dấu của đạo hàm cấp nhất: Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến của hàm số.
  6. Tìm cực trị: Xác định các điểm cực đại, cực tiểu của hàm số.
  7. Tính đạo hàm cấp hai (nếu cần): Tính đạo hàm f''(x) để xác định tính lồi, lõm của hàm số.
  8. Kết luận: Dựa vào bảng biến thiên và các điểm cực trị để kết luận về giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.

Lời giải chi tiết bài 2.6 trang 40

Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên đoạn [-1; 3])

Lời giải:

  • Bước 1: Hàm số f(x) = x3 - 3x2 + 2
  • Bước 2: Tập xác định: D = R
  • Bước 3: f'(x) = 3x2 - 6x
  • Bước 4: 3x2 - 6x = 0 => x = 0 hoặc x = 2
  • Bước 5: Lập bảng biến thiên:
    x-∞02+∞
    f'(x)+-+
    f(x)NBĐBNB
  • Bước 6: Hàm số đạt cực đại tại x = 0, f(0) = 2. Hàm số đạt cực tiểu tại x = 2, f(2) = -2.
  • Bước 7: f(-1) = -4, f(3) = 2
  • Bước 8: Vậy, giá trị lớn nhất của hàm số trên đoạn [-1; 3] là 2 (đạt tại x = 0 và x = 3), giá trị nhỏ nhất là -4 (đạt tại x = -1).

Mẹo giải nhanh và lưu ý quan trọng

  • Luôn kiểm tra kỹ tập xác định của hàm số trước khi tính đạo hàm.
  • Sử dụng bảng biến thiên để trực quan hóa sự biến đổi của hàm số.
  • Chú ý đến các điểm không xác định của hàm số (ví dụ: mẫu số bằng 0).
  • Thực hành nhiều bài tập để nắm vững các kỹ năng giải quyết.

Tusach.vn – Nơi đồng hành cùng bạn học Toán 11

Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách giáo khoa Toán 11 Kết nối tri thức. Hãy truy cập tusach.vn để học tập hiệu quả và đạt kết quả cao trong môn Toán!