Lựa chọn câu để xem lời giải nhanh hơn- Hoạt động
- Câu hỏi
- Luyện tập 1
- Luyện tập 2
- Vận dụng
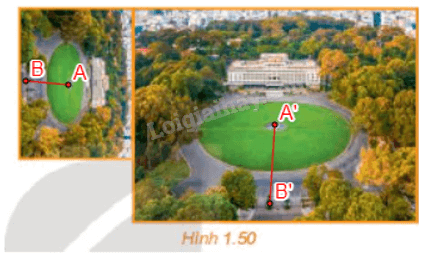
Hai tấm ảnh Dinh Thống Nhất ở hình trên giống nhau về hình dạng, chỉ khác nhau về kích thước.
a) Hãy đo và cho biết chiều dài, chiều rộng của tấm ảnh lớn tương ứng gấp mấy lần chiều dài, chiều rộng của tấm ảnh nhỏ.
b) Nếu lấy hai vị trí A, B bất kì thuộc tấm ảnh nhỏ và các vị trí A', B' tương ứng với chúng trên tấm ảnh lớn thì khoảng cách giữa A' và B' gấp mấy lần khoảng cách giữa A và B? Hãy lấy ví dụ cụ thể các vị trí và đo để kiểm tra câu trả lời của bạn.
Phương pháp giải:
Quan sát hình ảnh Dinh Thống Nhất để làm
Lời giải chi tiết:
a) Qua đo đạc, ta thấy chiều dài và chiều rộng của tấm ảnh lớn tương ứng gấp 2 lần chiều dài và chiều rộng của tấm ảnh nhỏ.
b) Lấy các điểm A, B và A', B' tương ứng như hình vẽ.

Qua đo đạc ta thấy A'B' = 2AB.
Phép dời hình và phép vị tự tỉ số t có phải là các phép đồng dạng hay không? Nếu có thì tỉ số đồng dạng là bao nhiêu?
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
+ Phép dời hình cũng là phép đồng dạng với tỉ số k = 1.
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép dời hình. Khi đó M'N' = MN (phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số 1.
+ Phép vị tự với tỉ số k là phép đồng dạng với tỉ số đồng dạng \(\left| k \right|\).
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép vị tự tỉ số k. Khi đó \(\overrightarrow {M'N'} = k\overrightarrow {MN} \). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số \(\left| k \right|{\rm{ }}\left( {\left| k \right| > 0} \right).\)
Chứng minh rằng phép biến hình có được bằng cách thực hiện liên tiếp phép đồng dạng f với tỉ số k1 và phép đồng dạng g với tỉ số k2 là một phép đồng dạng với tỉ số k1.k2.
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
Lấy hai điểm M, N bất kì. Gọi M', N' tương ứng là ảnh của M, N qua phép đồng dạng f với tỉ số k1 thì ta có M'N' = k1MN.
Gọi M", N" tương ứng là ảnh của M', N' qua phép đồng dạng g với tỉ số k2 thì ta có M"N" = k2M'N'.
Khi đó ta có M"N" = k2 M'N' = k2 . (k1MN) = (k1.k2)MN.
Do đó, M", N" tương ứng là ảnh của M, N qua phép đồng dạng với tỉ số k1.k2.
Từ đó suy ra điều phải chứng minh.
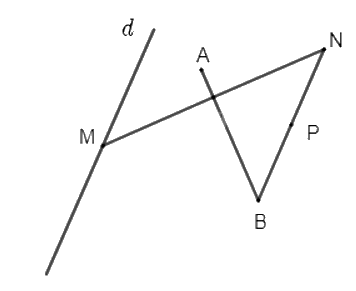
Cho đường thẳng d và hai điểm phân biệt A, B. Điểm M thay đổi trên đường thẳng d. Gọi N là điểm đối xứng của M qua đường thẳng AB và P là trung điểm của đoạn thẳng BN. Chứng minh rằng P thuộc một đường thẳng cố định.
Phương pháp giải:
Dựa vào kiến thức phép đối xứng, phép vị tự để trả lời
Lời giải chi tiết:

Vì N là điểm đối xứng của M qua đường thẳng AB nên ta có phép đối xứng trục AB biến điểm M thành điểm N.
Ta có P là trung điểm của BN nên \(\overrightarrow {BP} = \frac{1}{2}\overrightarrow {BN} \), do đó ta có phép vị tự tâm B, tỉ số \(\frac{1}{2}\) biến điểm N thành điểm P.
Như vậy, phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\frac{1}{2}} \right)}}\)biến điểm M thành điểm P.
Mặt khác M thuộc đường thẳng d cố định, A và B cố định, do đó P thuộc đường thẳng d' cố định là ảnh của đường thẳng d qua phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\frac{1}{2}} \right)}}\).
Vậy P thuộc một đường thẳng cố định.
Trong hai hình Dinh Thống Nhất ở Hình 1.50, hãy chỉ ra phép đồng dạng biến hình nhỏ thành hình lớn.

Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:

Phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc quay 90° và phép vị tự tâm O, tỉ số 2 biến hình Dinh Thống Nhất nhỏ thành hình Dinh Thống Nhất lớn với O là điểm trên hình vẽ.