Giải bài 1.8 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng quan nội dung
Giải bài 1.8 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài tập 1.8 trang 15 trong Chuyên đề học tập Toán 11 Kết nối tri thức. Chúng tôi sẽ trình bày các bước giải một cách rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập, cung cấp tài liệu và lời giải chính xác, cập nhật nhất.
Cho đường thẳng d và hai điểm phân biệt A, B sao cho đường thẳng AB không vuông góc với d.
Đề bài
Cho đường thẳng d và hai điểm phân biệt A, B sao cho đường thẳng AB không vuông góc với d. Gọi M, N tương ứng là các điểm đối xứng với A, B qua d. Hỏi A, B, M, N có là 4 đỉnh của một hình thang cân hay không?
Phương pháp giải - Xem chi tiết
Hình thang cân là hình thang có 2 cạnh bên hoặc 2 góc ở đáy bằng nhau.
Hình thang là tứ giác có một cặp cạnh song song.
Lời giải chi tiết
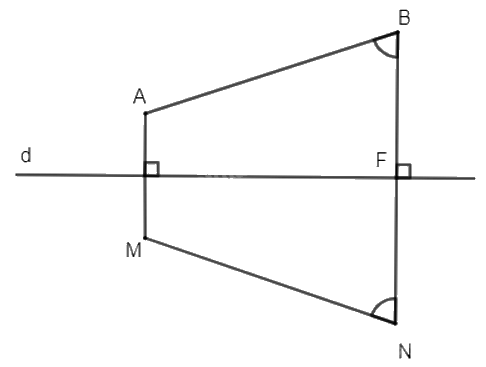
Vì M, N tương ứng là các điểm đối xứng với A, B qua d nên phép đối xứng trục d biến điểm A thành điểm M và biến điểm B thành điểm N. Do đó, d là đường trung trực của đoạn thẳng AM và đoạn thẳng BN. Suy ra AM // BN (vì cùng vuông góc với d).
Suy ra tứ giác AMNB là hình thang (1).
Gọi F là trung điểm của BN, khi đó F thuộc đường trung trực d của đoạn thẳng BN nên phép đối xứng trục d biến điểm F thành chính nó.
Từ đó suy ra phép đối xứng trục d biến góc ABF thành góc MNF nên \(\widehat {ABF} = \widehat {MNF}\) hay \(\widehat {ABN} = \widehat {MNB}\) (2).
Từ (1) và (2) suy ra tứ giác AMNB là hình thang cân.
Vậy A, B, M, N là 4 đỉnh của một hình thang cân.
Giải bài 1.8 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 1.8 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về dãy số, cấp số cộng và cấp số nhân. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Nội dung bài tập 1.8
Bài 1.8 yêu cầu chúng ta tìm số hạng tổng quát của dãy số (un) được xác định bởi công thức đệ quy hoặc công thức tường minh. Thông thường, bài tập sẽ cho trước một vài số hạng đầu tiên của dãy số và yêu cầu tìm mối liên hệ giữa các số hạng để xác định công thức tổng quát.
Phương pháp giải bài tập dãy số
Có nhiều phương pháp để giải bài tập dãy số, tùy thuộc vào dạng bài tập cụ thể. Một số phương pháp phổ biến bao gồm:
- Phương pháp quy nạp toán học: Sử dụng để chứng minh công thức tổng quát đúng với mọi n.
- Phương pháp tìm số hạng tổng quát bằng cách xét hiệu giữa các số hạng liên tiếp: Áp dụng khi dãy số là cấp số cộng hoặc cấp số nhân.
- Phương pháp sử dụng công thức tổng quát của cấp số cộng và cấp số nhân: Khi đã xác định được dãy số là cấp số cộng hoặc cấp số nhân.
- Phương pháp biến đổi đại số: Sử dụng các phép biến đổi đại số để tìm mối liên hệ giữa các số hạng và xác định công thức tổng quát.
Lời giải chi tiết bài 1.8 trang 15
Để giải bài 1.8 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức, chúng ta sẽ thực hiện các bước sau:
- Xác định dạng của dãy số: Quan sát các số hạng đầu tiên của dãy số để xác định xem dãy số có phải là cấp số cộng, cấp số nhân hay không.
- Tìm công thức tổng quát: Sử dụng các phương pháp đã nêu ở trên để tìm công thức tổng quát của dãy số.
- Kiểm tra lại kết quả: Thay các giá trị của n vào công thức tổng quát để kiểm tra xem kết quả có đúng với các số hạng đã cho hay không.
Ví dụ: Giả sử bài 1.8 cho dãy số (un) với u1 = 2 và un+1 = 2un + 1. Ta có thể tìm công thức tổng quát như sau:
- u1 = 2
- u2 = 2u1 + 1 = 2(2) + 1 = 5
- u3 = 2u2 + 1 = 2(5) + 1 = 11
- u4 = 2u3 + 1 = 2(11) + 1 = 23
Nhận thấy rằng un = 3 * 2n - 1. Ta có thể chứng minh công thức này bằng phương pháp quy nạp toán học.
Lưu ý khi giải bài tập dãy số
Khi giải bài tập dãy số, bạn cần lưu ý những điều sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài tập.
- Nắm vững các khái niệm cơ bản và các công thức liên quan.
- Sử dụng các phương pháp giải phù hợp với từng dạng bài tập.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn - Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn là một website cung cấp tài liệu học tập Toán 11 uy tín và chất lượng. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập của bạn!
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 1.8 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!