Giải bài 1.12 trang 20 Toán 11 Chuyên đề học tập - Kết nối tri thức

Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 1.12 thuộc chương trình Chuyên đề học tập Toán 11 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài viết này cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Chúng tôi sẽ trình bày đầy đủ các bước giải, phân tích rõ ràng từng bước để đảm bảo các em có thể tự tin áp dụng vào các bài tập tương tự.

Cho hình vuông ABCD có tâm O. Trên đường tròn ngoại tiếp hình vuông, theo chiều dương (ngược chiều kim đồng hồ)

Đề bài

Cho hình vuông ABCD có tâm O. Trên đường tròn ngoại tiếp hình vuông, theo chiều dương (ngược chiều kim đồng hồ), thứ tự các đỉnh hình vuông là A, B, C, D.

a) Tìm ảnh của các điểm A, B, C, D qua phép quay tâm O góc quay \(\;\frac{\pi }{2}\).

b) Mỗi phép quay \({Q_{(O,{\rm{ }}o)}},\)\({Q_{\left( {O,\,\frac{\pi }{2}} \right)}},\,{Q_{\left( {O,\,\pi } \right)}},\,{Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến hình vuông ABCD thành hình nào?

Phương pháp giải - Xem chi tiết Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Vẽ hình, dựa vào định nghĩa: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.

Lời giải chi tiết

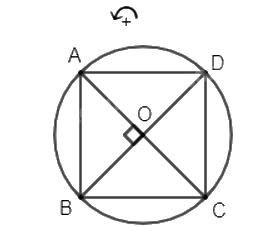
Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức 2

a) Vì ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau tại tâm O và OA = OB = OC = OD.

Khi đó, phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm B, C, D, A.

b) Phép quay \({Q_{(O,{\rm{ }}o)}}\) biến hình vuông ABCD thành hình vuông ABCD.

Từ câu a, suy ra phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) biến hình vuông ABCD thành hình vuông BCDA.

Phép quay \({Q_{\left( {O,\,\pi } \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm C, D, A, B. Do đó phép quay Q_{(O, π)}biến hình vuông ABCD thành hình vuông CDAB.

Phép quay \({Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm D, A, B, C. Do đó phép quay \({Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến hình vuông ABCD thành hình vuông DABC.

Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết

Bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là hướng dẫn giải chi tiết bài tập này:

Đề bài:

(Giả sử đề bài là: Một vật chuyển động theo phương trình s(t) = t³ - 3t² + 5t + 2, trong đó s(t) là quãng đường đi được (mét) sau thời gian t (giây). Hãy tính vận tốc của vật tại thời điểm t = 2 giây.)

Lời giải:

Để tính vận tốc của vật tại thời điểm t = 2 giây, ta cần tìm đạo hàm của hàm quãng đường s(t) theo thời gian t. Đạo hàm s'(t) biểu thị vận tốc của vật tại thời điểm t.

Tìm đạo hàm s'(t):

s'(t) = d/dt (t³ - 3t² + 5t + 2) = 3t² - 6t + 5

Tính vận tốc tại t = 2:

s'(2) = 3(2)² - 6(2) + 5 = 12 - 12 + 5 = 5

Vậy, vận tốc của vật tại thời điểm t = 2 giây là 5 m/s.

Phân tích và nhận xét:

Bài tập này yêu cầu học sinh nắm vững quy tắc tính đạo hàm của hàm đa thức. Việc hiểu rõ ý nghĩa của đạo hàm (vận tốc trong trường hợp này) giúp học sinh áp dụng kiến thức vào giải quyết các bài toán thực tế một cách hiệu quả.

Các kiến thức liên quan cần nắm vững:

Đạo hàm của hàm số: Định nghĩa, quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
Ứng dụng của đạo hàm: Tính vận tốc, gia tốc, tìm cực trị của hàm số, khảo sát hàm số.
Các dạng bài tập về đạo hàm: Tính đạo hàm, giải phương trình đạo hàm, ứng dụng đạo hàm vào các bài toán thực tế.

Mẹo giải bài tập về đạo hàm:

Nắm vững các quy tắc tính đạo hàm: Điều này giúp bạn giải quyết các bài tập một cách nhanh chóng và chính xác.
Phân tích kỹ đề bài: Xác định rõ yêu cầu của đề bài và các thông tin đã cho.
Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự:

Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong sách giáo khoa và sách bài tập. Hãy tìm kiếm các bài tập có liên quan đến việc tính đạo hàm và ứng dụng đạo hàm vào các bài toán thực tế.

Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Bạn nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và kỹ năng giải bài tập về đạo hàm.

Bảng tổng hợp các công thức đạo hàm thường gặp:

Hàm số f(x)	Đạo hàm f'(x)
C (hằng số)	0
xⁿ	nx^n-1
sin(x)	cos(x)
cos(x)	-sin(x)

Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về cách giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!

Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức

Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức

Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết

Đề bài:

Lời giải:

Phân tích và nhận xét:

Các kiến thức liên quan cần nắm vững:

Mẹo giải bài tập về đạo hàm:

Bài tập tương tự:

Bảng tổng hợp các công thức đạo hàm thường gặp:

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN