Lựa chọn câu để xem lời giải nhanh hơn- Hoạt động 2
- Luyện tập 2
- Luyện tập 3
- Vận dụng
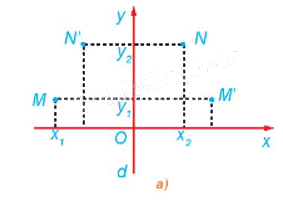
Cho phép đối xứng trục d biến M thành M', N thành N'. Xét hệ trục tọa độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có tọa độ là \(\left( {{x_1};{\rm{ }}{y_1}} \right),\) N có tọa độ là \(\left( {{x_2};{\rm{ }}{y_2}} \right).\)

a) Hãy cho biết tọa độ của M', N'.
b) Tính \(M{N^2},{\rm{ }}M'N{'^2}\;\) theo tọa độ của các điểm tương ứng.
c) So sánh độ dài các đoạn thẳng MN, M'N'.
Phương pháp giải:
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết:
a) M' và N' lần lượt là ảnh của M và N qua phép đối xứng trục d (trục Oy).
Do đó \(M'\left( {-{\rm{ }}{x_1};{\rm{ }}{y_1}} \right)\) và \(N'\left( {-{\rm{ }}{x_2};{\rm{ }}{y_2}} \right).\)
b) Ta có:
\(\begin{array}{l}M{N^2} = {\left( {\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} } \right)^2} = {\rm{ }}{({x_2}\;-{\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\\M'N{'^2} = {\left( {\sqrt {{{( - {x_2} - ( - {x_1}))}^2} + {{({y_2} - {y_1})}^2}} } \right)^2} = {\rm{ }}{-{\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}.\end{array}\)
c) Ta có: \({({x_2}\;-{\rm{ }}{x_1})^2}\; = {\rm{ }}{({x_1}\;-{\rm{ }}{x_2})^2}\; = {\rm{ }}{(-{\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}.\)
Do đó \({({x_2}\;-{\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\; = {\rm{ }}{({\rm{ }}{x_2}\; + {\rm{ }}{x_1})^2}\; + {\rm{ }}{({y_2}\;-{\rm{ }}{y_1})^2}\) hay \(M{N^2}\; = {\rm{ }}M'N{'^2}\)
Suy ra \(MN{\rm{ }} = {\rm{ }}M'N'.\)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – y – 1 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox.
Phương pháp giải:
- Lấy 2 điểm A, B thuộc d. Sau đó tìm ảnh của A, B qua phép đối xứng Ox là A’, B’. Ảnh của đường thẳng d chính là đường thẳng A’B’.
- Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Lời giải chi tiết:
Cách 1:
Lấy hai điểm A(0; – 1) và B(1; 2) thuộc d.
Gọi A', B' lần lượt là ảnh của A, B qua phép đối xứng trục Ox.
Khi đó A'(0; 1) và B'(1; – 2).
Vì d' là ảnh của đường thẳng d qua phép đối xứng trục Ox nên A' và B' thuộc d'.
Ta có: \(\overrightarrow {A'B'} = \left( {1;\, - 3} \right)\). Suy ra \(\overrightarrow {{n_{d'}}} = \left( {3;\,1} \right)\)
Vậy d' có phương trình là 3(x – 0) + (y – 1) = 0 hay 3x + y – 1 = 0.
Cách 2:
Gọi \(M'\left( {x';{\rm{ }}y'} \right)\) là ảnh của M(x; y) qua phép đối xứng trục Ox. Khi đó \(x'{\rm{ }} = {\rm{ }}x\) và \(y'{\rm{ }} = {\rm{ }}-{\rm{ }}y.\)
Ta có: \(M\; \in \;d\; \Leftrightarrow \;3x-y-1 = 0\; \Leftrightarrow \;3x'-\left( {-y'} \right)-1 = 0\; \Leftrightarrow \;3x' + {\rm{ }}y'-1{\rm{ }} = 0\;\;\)
Vậy M' thuộc đường thẳng d' có phương trình là \(3x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0.\)
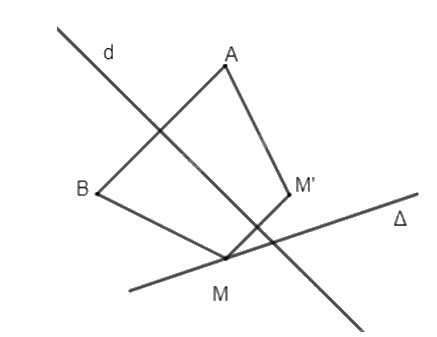
Cho đường thẳng \(\Delta \) và hai điểm A, B, sao cho \(\Delta \) không phải là đường trung trực của đoạn thẳng AB. Điểm M thay đổi trên \(\Delta \) (M không thuộc đường thẳng AB). Gọi M' là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thẳng cố định.
Phương pháp giải:
Chứng minh M' thay đổi trên một đường thẳng cố định \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
Lời giải chi tiết:
Gọi d là đường trung trực của đoạn thẳng AB. Vì AB cố định nên d cố định.
Do A, B, M, M' là 4 đỉnh của hình thang cân nhận AB là một cạnh đáy nên MM' là đáy còn lại của hình thang cân và đường trung trực d của đoạn thẳng AB cũng là đường trung trực của đoạn thẳng MM'. Do đó M' là ảnh của điểm M qua phép đối xứng trục d.
Mặt khác, M thuộc đường thẳng ∆ nên M' thuộc đường thẳng \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
Vậy rằng M' thay đổi trên một đường thẳng cố định \(\Delta \)' là ảnh của đường thẳng \(\Delta \) qua phép đối xứng trục d.
Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng.

Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
Quan sát hình ảnh ta thấy hình thứ hai từ trái sang có trục đối xứng.