Giải bài 2.18 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài tập 2.18 trang 49 trong Chuyên đề học tập Toán 11 Kết nối tri thức. Chúng tôi sẽ trình bày các bước giải một cách rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán!
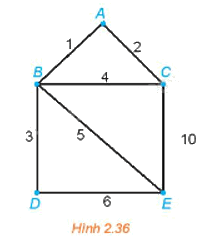
Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.36.
Giải bài 2.18 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 2.18 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về dãy số, cấp số cộng và cấp số nhân. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Đề bài:
Cho dãy số (un) xác định bởi u1 = 1 và un+1 = 2un + 1 với mọi n ≥ 1. Tính u5.
Lời giải:
Để tính u5, chúng ta sẽ tính lần lượt các số hạng của dãy số:
- u1 = 1 (đã cho)
- u2 = 2u1 + 1 = 2(1) + 1 = 3
- u3 = 2u2 + 1 = 2(3) + 1 = 7
- u4 = 2u3 + 1 = 2(7) + 1 = 15
- u5 = 2u4 + 1 = 2(15) + 1 = 31
Vậy, u5 = 31.
Phân tích và nhận xét:
Dãy số (un) có dạng un = 2n - 1. Chúng ta có thể chứng minh điều này bằng phương pháp quy nạp. Việc nhận ra công thức tổng quát của dãy số sẽ giúp chúng ta giải các bài toán tương tự một cách nhanh chóng và hiệu quả.
Mở rộng:
Bài tập này có thể được mở rộng bằng cách thay đổi công thức truy hồi un+1 = 2un + 1 thành một công thức khác, ví dụ như un+1 = aun + b, với a và b là các hằng số. Khi đó, chúng ta cần tìm công thức tổng quát của dãy số và sử dụng nó để giải các bài toán liên quan.
Các bài tập tương tự:
- Bài 2.19 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức
- Bài 2.20 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng kết:
Bài 2.18 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập cơ bản về dãy số. Việc nắm vững các khái niệm và công thức liên quan, cùng với việc luyện tập thường xuyên, sẽ giúp bạn giải quyết các bài toán tương tự một cách dễ dàng.
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài tập và củng cố kiến thức Toán 11. Hãy truy cập tusach.vn để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác!
| Số thứ tự | Công thức | Kết quả |
|---|
| 1 | u1 | 1 |
| 2 | u2 = 2u1 + 1 | 3 |
| 3 | u3 = 2u2 + 1 | 7 |
| 4 | u4 = 2u3 + 1 | 15 |
| 5 | u5 = 2u4 + 1 | 31 |