Giải bài 3.3 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng quan nội dung
Giải bài 3.3 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài 3.3 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trên hình chiếu của mỗi vật thể (H.3.27) còn thiếu một số nét. Bổ sung các nét còn thiếu đó.
Đề bài
Trên hình chiếu của mỗi vật thể (H.3.27) còn thiếu một số nét. Bổ sung các nét còn thiếu đó.
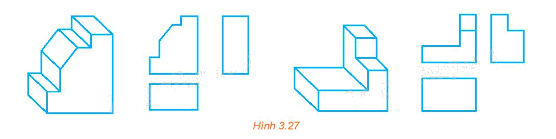
Phương pháp giải - Xem chi tiết
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết
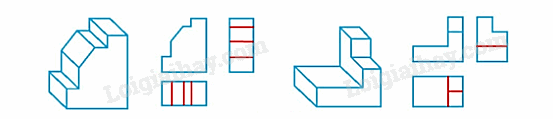
Bổ sung các nét còn thiếu trên hình chiếu của mỗi vật thể trong Hình 3.27 như sau:
Giải bài 3.3 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 3.3 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán cụ thể. Để giải bài này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
- Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần khảo sát.
- Tính đạo hàm: Sử dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm cấp nhất của hàm số.
- Tìm điểm cực trị: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số.
- Khảo sát hàm số: Dựa vào đạo hàm cấp hai để xác định tính chất của các điểm cực trị (cực đại, cực tiểu).
- Vẽ đồ thị hàm số: Sử dụng các thông tin đã tìm được để vẽ đồ thị hàm số.
Lời giải chi tiết bài 3.3 trang 65
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 3.3 trang 65, Tusach.vn xin trình bày lời giải chi tiết như sau:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Lời giải:
- Bước 1: Tính đạo hàm cấp nhất: y' = 3x2 - 6x
- Bước 2: Tìm điểm cực trị: Giải phương trình y' = 0, ta được: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Bước 3: Tính đạo hàm cấp hai: y'' = 6x - 6
- Bước 4: Xác định tính chất của điểm cực trị:
- Tại x = 0: y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0, ymax = 2
- Tại x = 2: y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, ymin = -2
Kết luận: Hàm số y = x3 - 3x2 + 2 đạt cực đại tại điểm (0, 2) và cực tiểu tại điểm (2, -2).
Các bài tập tương tự
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về đạo hàm và ứng dụng của đạo hàm, các em có thể tham khảo các bài tập tương tự sau:
- Bài 3.4 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức
- Bài 3.5 trang 67 Chuyên đề học tập Toán 11 Kết nối tri thức
- Các bài tập trong sách bài tập Toán 11 Kết nối tri thức
Lưu ý khi giải bài tập về đạo hàm
Khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:
- Nắm vững các quy tắc tính đạo hàm.
- Kiểm tra kỹ kết quả tính đạo hàm.
- Sử dụng đạo hàm cấp hai để xác định tính chất của các điểm cực trị.
- Vẽ đồ thị hàm số để kiểm tra lại kết quả.
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin giải bài 3.3 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức và các bài tập tương tự một cách hiệu quả.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với Tusach.vn để được hỗ trợ nhé!