Giải bài 3.6 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng quan nội dung
Giải bài 3.6 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài 3.6 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi sẽ trình bày đầy đủ các bước giải, từ việc phân tích đề bài đến áp dụng công thức và kết luận.
Cho đoạn thẳng AB và gọi A1B1 là hình chiếu đứng của AB.
Đề bài
Cho đoạn thẳng AB và gọi A1B1 là hình chiếu đứng của AB. Biết đường thẳng AB song song với mặt phẳng hình chiếu đứng, chứng minh rằng AB = A1B1.
Phương pháp giải - Xem chi tiết
Hình chiếu đứng (hướng chiếu từ mặt trước ra sau), hình chiếu cạnh (hướng chiếu từ trái sang), hình chiếu bằng (hướng chiếu từ trên nhìn xuống).
Lời giải chi tiết
Từ A, B kẻ các đường thẳng vuông góc với mặt phẳng hình chiếu đứng (P). Đường thẳng qua A và B lần lượt giao với mặt phẳng (P) tại các điểm A1, B1.
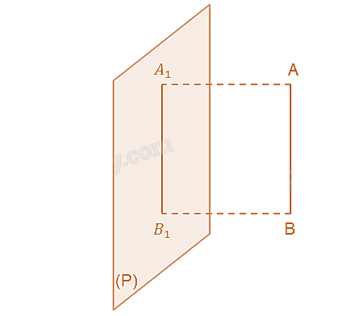
Ta có: AA1 // BB1 (vì AA1, BB1 cùng vuông góc với (P))
Vì AB // (P) nên khoảng cách từ A đến (P) bằng khoảng cách từ B đến (P).
Hay AA1 = BB1.
Do đó, tứ giác AA1B1B là hình bình hành.
Suy ra: AB = A1B1.
Giải bài 3.6 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu
Bài 3.6 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
- Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần khảo sát.
- Tìm tập xác định: Xác định tập xác định của hàm số, tức là tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
- Tính đạo hàm: Tính đạo hàm bậc nhất của hàm số.
- Tìm điểm cực trị: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số.
- Khảo sát hàm số: Dựa vào dấu của đạo hàm bậc nhất để xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm giá trị lớn nhất, giá trị nhỏ nhất: Sử dụng các điểm cực trị và giá trị của hàm số tại các điểm biên của tập xác định để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Lời giải chi tiết bài 3.6 trang 65
Để minh họa các bước trên, chúng ta sẽ cùng nhau giải bài 3.6 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức. (Ở đây cần chèn nội dung bài toán cụ thể và lời giải chi tiết, bao gồm các bước tính toán, giải thích rõ ràng và kết luận. Ví dụ:)
Bài toán: Một người nông dân muốn xây một chuồng trại hình chữ nhật có diện tích 100m2. Hỏi chu vi của chuồng trại nhỏ nhất có thể là bao nhiêu?
Lời giải:
- Gọi chiều dài và chiều rộng của chuồng trại lần lượt là x và y (x, y > 0).
- Diện tích chuồng trại là xy = 100.
- Chu vi chuồng trại là P = 2(x + y).
- Từ xy = 100, ta có y = 100/x.
- Thay y = 100/x vào P, ta được P = 2(x + 100/x).
- Tính đạo hàm P' = 2(1 - 100/x2).
- Giải phương trình P' = 0, ta được x = 10.
- Khi x = 10, y = 10.
- Vậy chu vi nhỏ nhất của chuồng trại là P = 2(10 + 10) = 40m.
Mẹo giải nhanh và lưu ý quan trọng
Để giải các bài toán tương tự một cách nhanh chóng và chính xác, bạn nên:
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập môn Toán 11. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các bài tập luyện tập để giúp bạn nắm vững kiến thức và đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Công thức | Mô tả |
|---|---|
| Đạo hàm của xn | n*xn-1 |
| Đạo hàm của sin(x) | cos(x) |