Giải bài 2.10 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng quan nội dung
Giải bài 2.10 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 2.10 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho các em.
Cho đồ thị G như Hình 27. Tìm một đường đi Hamilton từ S đến R.
Đề bài
Cho đồ thị G như Hình 27. Tìm một đường đi Hamilton từ S đến R.
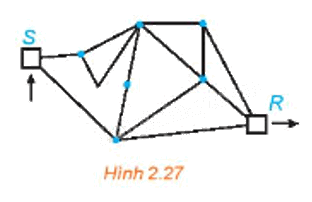
Phương pháp giải - Xem chi tiết
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết
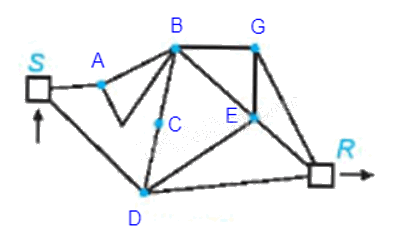
Đặt thêm tên các đỉnh vào đồ thị như hình vẽ trên.
Có thể thấy một đường đi Hamilton từ đỉnh S đến đỉnh R của đồ thị G là SABCDEGR.
Giải bài 2.10 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 2.10 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Nội dung bài tập 2.10
Bài 2.10 thường có dạng như sau: Cho hàm số f(x). Tìm giá trị của x để hàm số đạt cực đại hoặc cực tiểu. Hoặc, tìm khoảng đồng biến, nghịch biến của hàm số.
Phương pháp giải bài tập 2.10
- Bước 1: Tính đạo hàm f'(x): Sử dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của hàm số f(x).
- Bước 2: Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm dừng của hàm số.
- Bước 3: Lập bảng xét dấu f'(x): Xét dấu của f'(x) trên các khoảng xác định bởi các điểm dừng.
- Bước 4: Kết luận: Dựa vào bảng xét dấu f'(x) để kết luận về khoảng đồng biến, nghịch biến, cực đại, cực tiểu của hàm số.
Ví dụ minh họa giải bài 2.10 trang 44
Bài toán: Cho hàm số f(x) = x3 - 3x2 + 2. Tìm cực đại và cực tiểu của hàm số.
Giải:
- Bước 1: Tính đạo hàm: f'(x) = 3x2 - 6x
- Bước 2: Tìm điểm dừng: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Bước 3: Lập bảng xét dấu:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 4: Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu ý khi giải bài tập 2.10
- Luôn kiểm tra điều kiện xác định của hàm số trước khi tính đạo hàm.
- Chú ý các quy tắc tính đạo hàm của các hàm số đặc biệt (hàm lượng giác, hàm mũ, hàm logarit).
- Vẽ đồ thị hàm số để kiểm tra kết quả.
Các bài tập tương tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và kỹ năng giải bài tập.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải bài 2.10 trang 44 Chuyên đề học tập Toán 11 Kết nối tri thức một cách hiệu quả. Chúc các em học tập tốt!