Giải bài 3.7 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài 3.7 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp cho bạn đáp án chính xác và phương pháp giải bài tập hiệu quả.
Tusach.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp các tài liệu và giải bài tập chất lượng.
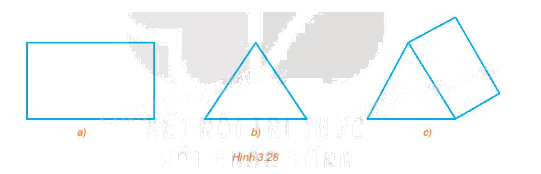
Trong các hình của Hình 3.28, hình nào là hình chiếu trục đo của hình lăng trụ tam giác?
Giải bài 3.7 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 3.7 trang 65 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài này, chúng ta cần nắm vững kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Đề bài:
Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy khảo sát hàm số và tìm các điểm cực trị.
Lời giải:
- Tính đạo hàm cấp nhất:
f'(x) = 3x2 - 6x
- Tìm điểm dừng:
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm dừng của hàm số.
- Khảo sát dấu của đạo hàm cấp nhất:
| x | -∞ | 0 | 2 | +∞ |
|---|
| f'(x) | + | - | + | + |
| f(x) | NB | ĐB | NB | NB |
(NB: Đồng biến, ĐB: Nghịch biến)
- Kết luận:
- Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Hàm số nghịch biến trên khoảng (0; 2).
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu ý quan trọng:
Khi giải các bài tập về khảo sát hàm số, bạn cần chú ý các bước sau:
- Xác định tập xác định của hàm số.
- Tính đạo hàm cấp nhất và đạo hàm cấp hai (nếu cần).
- Tìm điểm dừng và khảo sát dấu của đạo hàm cấp nhất để xác định khoảng đồng biến, nghịch biến.
- Tìm điểm uốn (nếu có).
- Xác định giới hạn của hàm số tại vô cùng và các điểm gián đoạn.
- Vẽ đồ thị hàm số.
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm sách giáo khoa, sách bài tập, đề thi và giải bài tập chi tiết. Chúng tôi luôn cập nhật những thông tin mới nhất và đảm bảo chất lượng nội dung để giúp bạn học tập hiệu quả.
Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác và đồng hành cùng chúng tôi trên con đường chinh phục tri thức!