Giải mục 2 trang 10, 11 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 10, 11 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 10, 11 của Chuyên đề học tập Toán 11 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu nhất.
Bài viết này sẽ giúp bạn hiểu rõ hơn về các khái niệm, định lý và phương pháp giải bài tập liên quan.
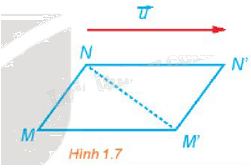
Phép tịnh tiến biến \({T_{\overrightarrow u }}\) iến M thành M', N thành N' (H.1.7).
Luyện tập 2
Cho đường tròn (O; R) và điểm O' khác điểm O. Với mỗi điểm M thuộc (O; R) sao cho O, O', M không thẳng hàng, vẽ hình bình hành MOO'M'. Hỏi khi M thay đổi trên (O; R) thì M' thay đổi trên đường nào?
Phương pháp giải:
Vẽ hình và chứng minh M’ thay đổi trên trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Lời giải chi tiết:
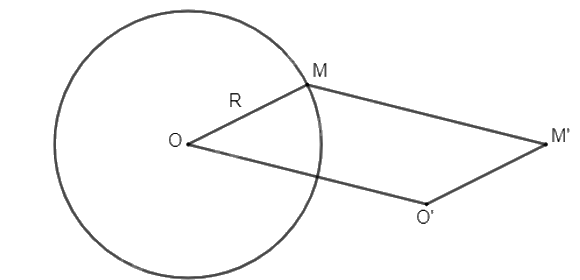
Ta có: MOO'M' là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {O'M'} \) và \(\overrightarrow {OO'} = \overrightarrow {MM'} \)
Vì OM = R nên \(O'M' = \left| {\overrightarrow {O'M'} } \right| = \left| {\overrightarrow {OM} } \right| = OM = R\) , R cố định nên O' luôn cách M' một khoảng không đổi bằng R.
Do O, O' cố định và \(\overrightarrow {OO'} = \overrightarrow {MM'} \) nên phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến điểm M thành điểm M'. Suy ra nếu M thay đổi trên (O; R) thì M' luôn là ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Lại có phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến đường tròn (O; R) thành đường tròn có bán kính là R và có tâm là ảnh của tâm O qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) hay chính là điểm O'. Điều này có nghĩa là đường tròn (O'; R) là ảnh của đường tròn (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Mà O'M' = R không đổi nên M' luôn thuộc đường tròn (O'; R).
Vậy khi M thay đổi trên (O; R) thì M' thay đổi trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Hoạt động 2
Phép tịnh tiến biến \({T_{\overrightarrow u }}\) iến M thành M', N thành N' (H.1.7).
a) Có nhận xét gì về \(\overrightarrow {MM'} + \overrightarrow {M'M} \) và \(\overrightarrow {M'N} + \overrightarrow {NN'} \)
b) Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {M'N'} \).
Phương pháp giải:
Quan sát hình vẽ, áp dụng quy tắc 3 điểm điểm làm.
Lời giải chi tiết:
a) Phép tịnh tiến \({T_{\overrightarrow u }}\) biến điểm M thành M' thì \(\overrightarrow {MM'} = \overrightarrow u \) và biến N thành N' thì \(\overrightarrow {NN'} = \vec u\).
Ta có: \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow u + \overrightarrow {M'N} \) và \(\overrightarrow {M'N} + \overrightarrow {NN'} = \overrightarrow {M'N} + \overrightarrow u \)
Do đó, \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
b) Theo quy tắc ba điểm ta có: \(\overrightarrow {MN} = \overrightarrow {MM'} + \overrightarrow {M'N} \) và \(\overrightarrow {M'N'} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
Mà theo câu a) ta có: \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
Do đó, \(\overrightarrow {MN} = \overrightarrow {M'N'} \)
Vận dụng 2
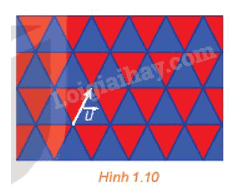
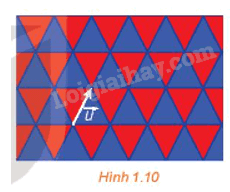
Trong việc lát mặt phẳng bởi các tam giác đều bằng nhau như được thể hiện trong Hình 1.10, phép tịnh tiến theo vectơ \(\vec u\) có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không?
Phương pháp giải:
Quan sát hình vẽ, dựa vào định nghĩa: Cho vectơ \(\overrightarrow u \). Phép hiến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \) gọi là phép tịnh tiến theo \(\overrightarrow u \), kí hiệu \({T_{\overrightarrow u }}\). Vectơ \(\overrightarrow u \) được gọi là vectơ tịnh tiến.
Lời giải chi tiết:
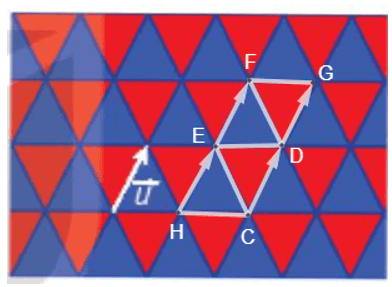
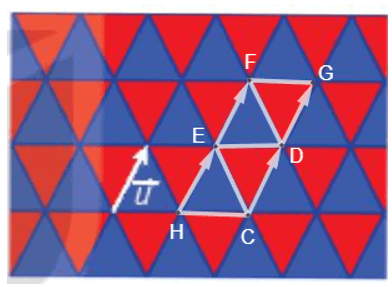
Đặt một số điểm như hình vẽ.
Ta thấy: \(\overrightarrow {HE} = \overrightarrow u ,\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm H, C, E tương ứng thành E, D, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác HCE thành tam giác EDF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu xanh thành một viên gạch màu xanh. Đối với các viên gạch màu xanh khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu xanh thành một viên gạch màu xanh. Ta cũng có: \(\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {DG} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm C, D, E tương ứng thành D, G, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác CDE thành tam giác DGF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu đỏ thành một viên gạch màu đỏ. Đối với các viên gạch màu đỏ khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu đỏ thành một viên gạch màu đỏ.
- Hoạt động 2
- Luyện tập 2
- Vận dụng 2
Phép tịnh tiến biến \({T_{\overrightarrow u }}\) iến M thành M', N thành N' (H.1.7).
a) Có nhận xét gì về \(\overrightarrow {MM'} + \overrightarrow {M'M} \) và \(\overrightarrow {M'N} + \overrightarrow {NN'} \)
b) Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {M'N'} \).
Phương pháp giải:
Quan sát hình vẽ, áp dụng quy tắc 3 điểm điểm làm.
Lời giải chi tiết:
a) Phép tịnh tiến \({T_{\overrightarrow u }}\) biến điểm M thành M' thì \(\overrightarrow {MM'} = \overrightarrow u \) và biến N thành N' thì \(\overrightarrow {NN'} = \vec u\).
Ta có: \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow u + \overrightarrow {M'N} \) và \(\overrightarrow {M'N} + \overrightarrow {NN'} = \overrightarrow {M'N} + \overrightarrow u \)
Do đó, \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
b) Theo quy tắc ba điểm ta có: \(\overrightarrow {MN} = \overrightarrow {MM'} + \overrightarrow {M'N} \) và \(\overrightarrow {M'N'} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
Mà theo câu a) ta có: \(\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \)
Do đó, \(\overrightarrow {MN} = \overrightarrow {M'N'} \)
Cho đường tròn (O; R) và điểm O' khác điểm O. Với mỗi điểm M thuộc (O; R) sao cho O, O', M không thẳng hàng, vẽ hình bình hành MOO'M'. Hỏi khi M thay đổi trên (O; R) thì M' thay đổi trên đường nào?
Phương pháp giải:
Vẽ hình và chứng minh M’ thay đổi trên trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Lời giải chi tiết:
Ta có: MOO'M' là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {O'M'} \) và \(\overrightarrow {OO'} = \overrightarrow {MM'} \)
Vì OM = R nên \(O'M' = \left| {\overrightarrow {O'M'} } \right| = \left| {\overrightarrow {OM} } \right| = OM = R\) , R cố định nên O' luôn cách M' một khoảng không đổi bằng R.
Do O, O' cố định và \(\overrightarrow {OO'} = \overrightarrow {MM'} \) nên phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến điểm M thành điểm M'. Suy ra nếu M thay đổi trên (O; R) thì M' luôn là ảnh của điểm M qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Lại có phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) biến đường tròn (O; R) thành đường tròn có bán kính là R và có tâm là ảnh của tâm O qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \) hay chính là điểm O'. Điều này có nghĩa là đường tròn (O'; R) là ảnh của đường tròn (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Mà O'M' = R không đổi nên M' luôn thuộc đường tròn (O'; R).
Vậy khi M thay đổi trên (O; R) thì M' thay đổi trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ \(\overrightarrow {OO'} \).
Trong việc lát mặt phẳng bởi các tam giác đều bằng nhau như được thể hiện trong Hình 1.10, phép tịnh tiến theo vectơ \(\vec u\) có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không?
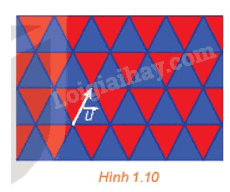
Phương pháp giải:
Quan sát hình vẽ, dựa vào định nghĩa: Cho vectơ \(\overrightarrow u \). Phép hiến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \) gọi là phép tịnh tiến theo \(\overrightarrow u \), kí hiệu \({T_{\overrightarrow u }}\). Vectơ \(\overrightarrow u \) được gọi là vectơ tịnh tiến.
Lời giải chi tiết:
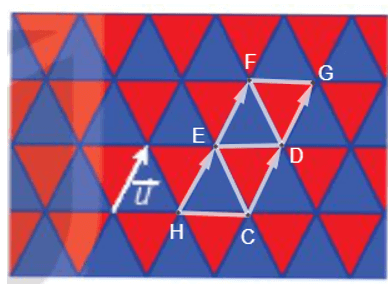
Đặt một số điểm như hình vẽ.
Ta thấy: \(\overrightarrow {HE} = \overrightarrow u ,\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm H, C, E tương ứng thành E, D, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác HCE thành tam giác EDF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu xanh thành một viên gạch màu xanh. Đối với các viên gạch màu xanh khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu xanh thành một viên gạch màu xanh. Ta cũng có: \(\overrightarrow {CD} = \overrightarrow u ,\overrightarrow {DG} = \overrightarrow u ,\overrightarrow {EF} = \overrightarrow u \) nên phép tịnh tiến \({T_{\overrightarrow u }}\) biến các điểm C, D, E tương ứng thành D, G, F. Do đó, \({T_{\overrightarrow u }}\) biến tam giác CDE thành tam giác DGF hay phép tịnh tiến theo vectơ \(\overrightarrow u \) biến một viên gạch màu đỏ thành một viên gạch màu đỏ. Đối với các viên gạch màu đỏ khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ \(\overrightarrow u \) biến mỗi viên gạch màu đỏ thành một viên gạch màu đỏ.
Giải mục 2 trang 10, 11 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trong mục này không chỉ giúp củng cố lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng vô cùng quan trọng trong học tập và cuộc sống.
Nội dung chính của Mục 2 (trang 10, 11)
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định chính xác nội dung mà nó đề cập đến. Thông thường, đây có thể là một trong các chủ đề sau:
- Hàm số lượng giác: Biến đổi lượng giác, đồ thị hàm số lượng giác, phương trình lượng giác.
- Đạo hàm: Các quy tắc tính đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số.
- Giới hạn: Tính giới hạn của hàm số, các dạng giới hạn đặc biệt.
- Hình học giải tích: Phương trình đường thẳng, đường tròn, elip, hypebol, parabol.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập thường gặp trong Mục 2 trang 10, 11 Chuyên đề học tập Toán 11 - Kết nối tri thức. (Lưu ý: Nội dung cụ thể sẽ phụ thuộc vào chủ đề của Mục 2)
Ví dụ 1: Giải phương trình lượng giác
Giả sử phương trình cần giải là: sin(x) = 1/2
- Xác định các nghiệm tổng quát: Nghiệm tổng quát của phương trình sin(x) = a là
x = arcsin(a) + k2πhoặcx = π - arcsin(a) + k2π, với k là số nguyên. - Tìm các nghiệm trong khoảng yêu cầu: Thay các giá trị của k vào nghiệm tổng quát để tìm các nghiệm nằm trong khoảng yêu cầu của bài toán.
Ví dụ 2: Tính đạo hàm của hàm số
Giả sử hàm số cần tính đạo hàm là: f(x) = x^2 + 3x - 1
Áp dụng quy tắc tính đạo hàm của tổng và tích, ta có:
f'(x) = 2x + 3Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong Mục 2 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Nắm vững các công thức, định lý: Đây là nền tảng cơ bản để giải quyết mọi bài toán.
- Phân tích kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và các điều kiện ràng buộc.
- Sử dụng các phương pháp giải phù hợp: Tùy thuộc vào từng bài toán cụ thể, bạn có thể sử dụng các phương pháp giải khác nhau, như phương pháp đại số, phương pháp hình học, phương pháp đồ thị,...
- Kiểm tra lại kết quả: Sau khi giải xong bài toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
- Sách bài tập Toán 11: Cung cấp nhiều bài tập đa dạng và phong phú để luyện tập.
- Các trang web học Toán trực tuyến: Tusach.vn, Vietjack, Loigiaihay,...
- Các video bài giảng Toán 11: Giúp bạn hiểu rõ hơn về các khái niệm và phương pháp giải bài tập.
Kết luận
Giải mục 2 trang 10, 11 Chuyên đề học tập Toán 11 - Kết nối tri thức đòi hỏi sự kiên trì, cẩn thận và nắm vững kiến thức nền tảng. Hy vọng rằng với những hướng dẫn chi tiết và mẹo giải nhanh mà Tusach.vn đã cung cấp, bạn sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt trong môn Toán.