Giải mục 1 trang 46 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 46 Chuyên đề học tập Toán 11 - Kết nối tri thức
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho mục 1 trang 46 trong Chuyên đề học tập Toán 11 - Kết nối tri thức.
Chúng tôi sẽ đi qua từng bước giải, giải thích rõ ràng các khái niệm và công thức liên quan, giúp bạn hiểu sâu sắc kiến thức và tự tin giải các bài tập tương tự.
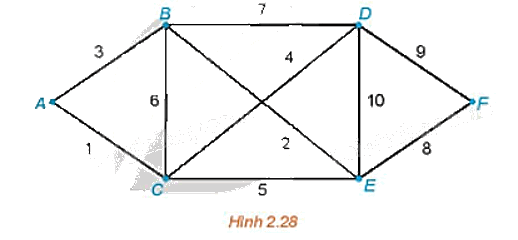
Cho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau bởi các con đường với độ dài của mỗi con đường được cho như trên hình.
Đề bài
Cho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau bởi các con đường với độ dài của mỗi con đường được cho như trên hình.
a) Hãy chỉ ra 2 đường đi từ A đến F và so sánh độ dài của hai đường đi đó.
b) Với mỗi đỉnh V của sơ đồ trên Hình 2.28, ta gắn số I(V) là khoảng cách ngắn nhất để đi từ A đến V và gọi là nhãn vĩnh viễn của đỉnh V. Như vậy, ta có ngay I(A) = 0. Dựa vào Hình 2.28, hãy tìm các nhãn vĩnh viễn I(B), I(C) của hai đỉnh kề với A là B, C.
Phương pháp giải - Xem chi tiết
Quan sát hình 2.28 để trả lời
Lời giải chi tiết
a) Hai đường đi từ A đến F, chẳng hạn là ABEF và ACEF.
Độ dài của đường đi ABEF là AB + BE + EF = 3 + 2 + 8 = 13.
Độ dài của đường đi ACEF là AC + CE + EF = 1 + 5 + 8 = 14.
Do đó, đường đi ABEF có độ dài ngắn hơn đường đi ACEF.
b) I(B) và I(C) lần lượt là các khoảng cách ngắn nhất để đi từ A đến B và C.
Ta có I(B) = AB = 3, I(C) = AC = 1.
Giải mục 1 trang 46 Chuyên đề học tập Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết
Mục 1 trang 46 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, ví dụ như đạo hàm của hàm số, ứng dụng đạo hàm trong việc khảo sát hàm số, hoặc các bài toán liên quan đến giới hạn. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Nội dung chính của Mục 1 trang 46
Để giải quyết các bài tập trong mục này, bạn cần hiểu rõ các khái niệm sau:
- Đạo hàm: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm.
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
- Ứng dụng đạo hàm: Khảo sát hàm số (tìm cực trị, điểm uốn, khoảng đơn điệu), giải phương trình, giải bất phương trình.
Ví dụ minh họa và lời giải chi tiết
Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1. Chúng ta sẽ áp dụng quy tắc tính đạo hàm của tổng và đạo hàm của hàm số lũy thừa:
f'(x) = 3x2 + 4x - 5
Một ví dụ khác, bài tập yêu cầu tìm cực trị của hàm số g(x) = x2 - 4x + 3. Chúng ta sẽ thực hiện các bước sau:
- Tính đạo hàm g'(x) = 2x - 4
- Giải phương trình g'(x) = 0 để tìm điểm cực trị: 2x - 4 = 0 => x = 2
- Xác định loại cực trị bằng cách xét dấu đạo hàm cấp hai g''(x) = 2 > 0. Vì g''(2) > 0 nên x = 2 là điểm cực tiểu.
- Tính giá trị cực tiểu: g(2) = 22 - 4*2 + 3 = -1
Mẹo giải bài tập hiệu quả
- Nắm vững định nghĩa và công thức: Đây là nền tảng để giải quyết mọi bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm giải toán có thể giúp bạn kiểm tra kết quả và tiết kiệm thời gian.
- Phân tích kỹ đề bài: Đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa và chuyên đề học tập, bạn có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
- Các video hướng dẫn giải Toán trên YouTube
Kết luận
Giải mục 1 trang 46 Chuyên đề học tập Toán 11 - Kết nối tri thức đòi hỏi sự hiểu biết vững chắc về kiến thức nền tảng và kỹ năng giải bài tập. Hy vọng với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả trên đây, bạn sẽ tự tin chinh phục các bài tập Toán 11 và đạt kết quả tốt nhất.