Giải bài 2.11 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức
Tổng quan nội dung
Giải bài 2.11 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 2.11 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn \(\frac{n}{2}\)
Đề bài
Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn \(\frac{n}{2}\) trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn \(\frac{{n - 1}}{2}\)”.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức vừa học để làm
Lời giải chi tiết
Cho đơn đồ thị G có 5 đỉnh như hình vẽ sau:
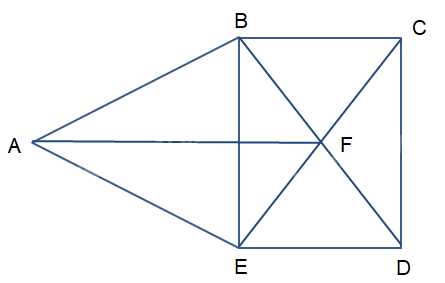
Mỗi đỉnh của đồ thị này đều có bậc là 2 hoặc 3, đều không nhỏ hơn \(\frac{{5 - 1}}{2} = 2\), thỏa mãn điều kiện của định lí Dirac nếu thay điều kiện “bậc của mỗi đỉnh của đồ thị G không nhỏ hơn \(\frac{n}{2}\)” bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn \(\frac{{n - 1}}{2}\)”.
Định lí Dirac là một điều kiện đủ cho sự tồn tại chu trình Hamilton, nhưng đồ thị trên lại không có chu trình Hamilton. Do vậy, đây vì ví dụ cần đưa ra để chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn \(\frac{n}{2}\) trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn \(\frac{{n - 1}}{2}\)”.
Giải bài 2.11 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 2.11 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về dãy số, cấp số cộng và cấp số nhân. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Nội dung bài tập 2.11 trang 45
Bài tập yêu cầu chúng ta tìm số hạng tổng quát của dãy số (un) được xác định bởi:
- u1 = 5
- un+1 = un + 3
Phương pháp giải bài tập
Để tìm số hạng tổng quát của dãy số, chúng ta có thể sử dụng phương pháp quy nạp toán học hoặc phương pháp tìm công thức trực tiếp.
Cách 1: Sử dụng phương pháp quy nạp toán học
- Bước 1: Kiểm tra với n = 1
- Bước 2: Giả sử công thức đúng với n = k
- Bước 3: Chứng minh công thức đúng với n = k+1
- Kết luận:
Với n = 1, ta có u1 = 5, phù hợp với công thức.
Giả sử uk = 5 + 3(k-1) đúng.
Ta cần chứng minh uk+1 = 5 + 3k.
Ta có: uk+1 = uk + 3 = (5 + 3(k-1)) + 3 = 5 + 3k - 3 + 3 = 5 + 3k.
Vậy công thức đúng với n = k+1.
Theo nguyên lý quy nạp toán học, công thức un = 5 + 3(n-1) đúng với mọi n ≥ 1.
Cách 2: Tìm công thức trực tiếp
Dãy số (un) là một cấp số cộng với u1 = 5 và công sai d = 3. Do đó, số hạng tổng quát của dãy số là:
un = u1 + (n-1)d = 5 + (n-1)3 = 5 + 3n - 3 = 3n + 2.
Kết luận
Vậy số hạng tổng quát của dãy số (un) là un = 3n + 2.
Các bài tập tương tự
Để luyện tập thêm, các em có thể giải các bài tập tương tự sau:
- Bài 2.12 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức
- Bài 2.13 trang 45 Chuyên đề học tập Toán 11 Kết nối tri thức
Lưu ý: Khi giải bài tập, các em nên đọc kỹ đề bài, xác định đúng các yếu tố cần tìm và lựa chọn phương pháp giải phù hợp. Nếu gặp khó khăn, các em có thể tham khảo lời giải chi tiết trên tusach.vn hoặc hỏi thầy cô giáo.
| n | un |
|---|---|
| 1 | 5 |
| 2 | 8 |
| 3 | 11 |
Chúc các em học tập tốt!