Giải mục 2 trang 6, 7, 8 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 6, 7, 8 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 6, 7, 8 của Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng nắm bắt kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đảm bảo cung cấp cho bạn nguồn tài liệu học tập đáng tin cậy.
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm (Mleft( {x;{rm{ }}y} right)) thành điểm (M'left( {x{rm{ }} + {rm{ }}1;{rm{ }}y{rm{ }} + {rm{ }}2} right).)
Hoạt động 2
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm \(M'\left( {x{\rm{ }} + {\rm{ }}1;{\rm{ }}y{\rm{ }} + {\rm{ }}2} \right).\)
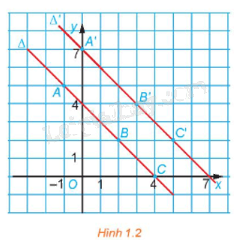
a) Xét các điểm \(A\left( {-{\rm{ }}1;{\rm{ }}5} \right),{\rm{ }}B\left( {2;{\rm{ }}2} \right),{\rm{ }}C\left( {4;{\rm{ }}0} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\). Xác định các ảnh của chúng qua f.
b) Chứng minh rằng nếu \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) là điểm thuộc đường thẳng \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) thì ảnh \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) của nó thuộc đường thẳng \(\Delta ':{\rm{ }}x + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\;\;\)
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
a) Ảnh của điểm A(– 1; 5) qua phép biến hình f là điểm \(A'\left( {-{\rm{ }}1{\rm{ }} + {\rm{ }}1;{\rm{ }}5{\rm{ }} + {\rm{ }}2} \right)\) hay \(A'\left( {0;{\rm{ }}7} \right).\)
Ảnh của điểm B(2; 3) qua phép biến hình f là điểm \(B'\left( {2{\rm{ }} + {\rm{ }}1;{\rm{ }}3{\rm{ }} + {\rm{ }}2} \right)\) hay \(B'\left( {3;{\rm{ }}5} \right).\)
Ảnh của điểm C(4; 0) qua phép biến hình f là điểm \(C'\left( {4{\rm{ }} + {\rm{ }}1;{\rm{ }}0{\rm{ }} + {\rm{ }}2} \right)\) hay \(C'\left( {5;{\rm{ }}2} \right).\)
b) Vì \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) nên \({x_0}\; + {\rm{ }}{y_0}\;-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) hay \({x_0}\; + {\rm{ }}{y_{0\;}} = {\rm{ }}4\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;{x_0}\; + {\rm{ }}{y_0}\; + {\rm{ }}3{\rm{ }} = {\rm{ }}4{\rm{ }} + {\rm{ }}3}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}7}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0}\end{array}\)
Suy ra \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) thuộc đường thẳng \(\Delta ':{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\)
Vận dụng 1
Quan sát ba tấm ảnh hoa hồng ở Hình 1.4, hãy cho biết hình nào giống ảnh của hình ở giữa qua một phép co về trục.

Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Quan sát Hình 1.4, ta thấy hình phía bên phải hình ở giữa giống ảnh của hình ở giữa qua một phép co về trục.
- Hoạt động 2
- Vận dụng 1
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm \(M'\left( {x{\rm{ }} + {\rm{ }}1;{\rm{ }}y{\rm{ }} + {\rm{ }}2} \right).\)
a) Xét các điểm \(A\left( {-{\rm{ }}1;{\rm{ }}5} \right),{\rm{ }}B\left( {2;{\rm{ }}2} \right),{\rm{ }}C\left( {4;{\rm{ }}0} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\). Xác định các ảnh của chúng qua f.
b) Chứng minh rằng nếu \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) là điểm thuộc đường thẳng \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) thì ảnh \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) của nó thuộc đường thẳng \(\Delta ':{\rm{ }}x + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\;\;\)

Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
a) Ảnh của điểm A(– 1; 5) qua phép biến hình f là điểm \(A'\left( {-{\rm{ }}1{\rm{ }} + {\rm{ }}1;{\rm{ }}5{\rm{ }} + {\rm{ }}2} \right)\) hay \(A'\left( {0;{\rm{ }}7} \right).\)
Ảnh của điểm B(2; 3) qua phép biến hình f là điểm \(B'\left( {2{\rm{ }} + {\rm{ }}1;{\rm{ }}3{\rm{ }} + {\rm{ }}2} \right)\) hay \(B'\left( {3;{\rm{ }}5} \right).\)
Ảnh của điểm C(4; 0) qua phép biến hình f là điểm \(C'\left( {4{\rm{ }} + {\rm{ }}1;{\rm{ }}0{\rm{ }} + {\rm{ }}2} \right)\) hay \(C'\left( {5;{\rm{ }}2} \right).\)
b) Vì \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) nên \({x_0}\; + {\rm{ }}{y_0}\;-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) hay \({x_0}\; + {\rm{ }}{y_{0\;}} = {\rm{ }}4\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;{x_0}\; + {\rm{ }}{y_0}\; + {\rm{ }}3{\rm{ }} = {\rm{ }}4{\rm{ }} + {\rm{ }}3}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}7}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0}\end{array}\)
Suy ra \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) thuộc đường thẳng \(\Delta ':{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\)
Quan sát ba tấm ảnh hoa hồng ở Hình 1.4, hãy cho biết hình nào giống ảnh của hình ở giữa qua một phép co về trục.

Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Quan sát Hình 1.4, ta thấy hình phía bên phải hình ở giữa giống ảnh của hình ở giữa qua một phép co về trục.
Giải mục 2 trang 6, 7, 8 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết
Mục 2 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt vào giải bài tập. Việc hiểu rõ bản chất của vấn đề và lựa chọn phương pháp giải phù hợp là yếu tố then chốt để đạt kết quả tốt.
Nội dung chính của Mục 2 (Trang 6, 7, 8)
Để giải quyết hiệu quả các bài tập trong mục này, trước tiên chúng ta cần xác định rõ nội dung chính mà chuyên đề hướng tới. Thông thường, mục 2 sẽ đi sâu vào:
- Các khái niệm cơ bản: Định nghĩa, tính chất, các dạng toán thường gặp.
- Các định lý quan trọng: Phát biểu, chứng minh và ứng dụng của các định lý.
- Phương pháp giải toán: Các bước thực hiện, các kỹ năng cần thiết để giải quyết bài toán.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 2 trang 6, 7, 8 Chuyên đề học tập Toán 11 - Kết nối tri thức:
Bài 1: (Trang 6)
(Giả sử bài 1 yêu cầu tính giới hạn của một hàm số)
- Phân tích đề bài: Xác định hàm số cần tính giới hạn và điểm mà tại đó cần tính giới hạn.
- Áp dụng kiến thức: Sử dụng các quy tắc tính giới hạn, các công thức giới hạn đặc biệt hoặc các phương pháp biến đổi đại số để đơn giản hóa biểu thức.
- Tính toán: Thực hiện các phép tính để tìm ra giá trị giới hạn.
- Kết luận: Viết kết quả cuối cùng và kiểm tra lại tính hợp lý.
Bài 2: (Trang 7)
(Giả sử bài 2 yêu cầu chứng minh một đẳng thức lượng giác)
Để chứng minh một đẳng thức lượng giác, chúng ta có thể sử dụng các phương pháp sau:
- Biến đổi tương đương: Sử dụng các công thức lượng giác để biến đổi một vế của đẳng thức về vế còn lại.
- Chứng minh bằng phương pháp phản chứng: Giả sử đẳng thức không đúng và dẫn đến mâu thuẫn.
Bài 3: (Trang 8)
(Giả sử bài 3 yêu cầu giải một phương trình lượng giác)
Khi giải phương trình lượng giác, chúng ta cần:
- Biến đổi phương trình: Sử dụng các công thức lượng giác để đưa phương trình về dạng đơn giản hơn.
- Tìm nghiệm: Xác định các giá trị của biến số thỏa mãn phương trình.
- Kiểm tra nghiệm: Đảm bảo rằng các nghiệm tìm được không phải là nghiệm ngoại lai.
Lưu ý quan trọng
Trong quá trình giải toán, hãy luôn:
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài toán trước khi bắt đầu giải.
- Sử dụng kiến thức một cách linh hoạt: Áp dụng các công thức, định lý và phương pháp giải phù hợp với từng bài toán cụ thể.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả cuối cùng là chính xác và hợp lý.
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách giáo khoa và chuyên đề Toán 11. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kiến thức của bạn!
| Bài tập | Trang | Mức độ khó |
|---|---|---|
| Bài 1 | 6 | Dễ |
| Bài 2 | 7 | Trung bình |
| Bài 3 | 8 | Khó |
| Nguồn: Tusach.vn | ||