Giải mục 1 trang 41, 42 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết mục 1 trang 41, 42 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật nhanh chóng nhất.
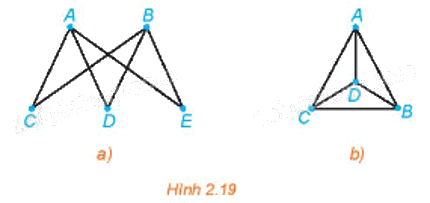
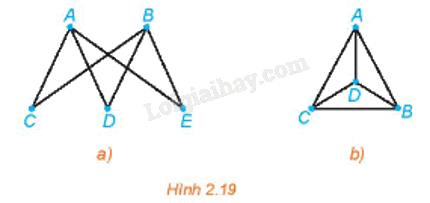
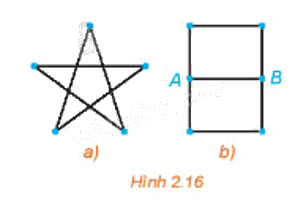
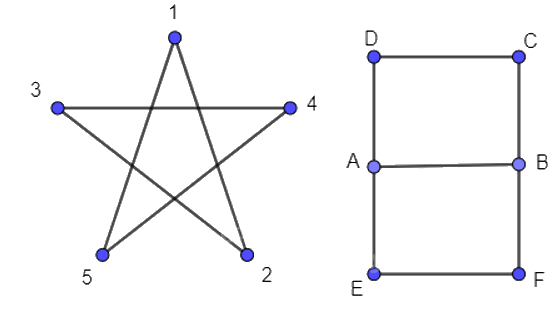
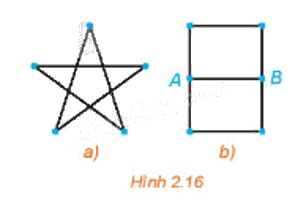
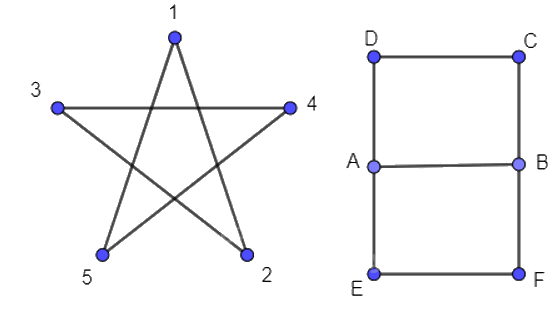
Hãy thử vẽ mỗi hình trên Hình 2.16 bằng một nét liền.
Giải mục 1 trang 41, 42 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 trang 41, 42 Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một phần kiến thức cụ thể trong chương trình. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa, định lý và công thức liên quan. Bài viết này sẽ đi sâu vào phân tích chi tiết từng bài tập, cung cấp lời giải dễ hiểu và các lưu ý quan trọng.
Nội dung chính của Mục 1 trang 41, 42
Thông thường, mục này sẽ đề cập đến các nội dung sau (tùy thuộc vào chuyên đề cụ thể):
- Khái niệm cơ bản: Định nghĩa, tính chất của các đối tượng toán học.
- Công thức: Các công thức quan trọng cần ghi nhớ và áp dụng.
- Phương pháp giải: Các bước giải bài tập, các kỹ năng cần thiết.
- Ví dụ minh họa: Các bài tập mẫu với lời giải chi tiết.
Bài tập 1: (Ví dụ - cần thay thế bằng nội dung thực tế của trang 41)
Đề bài: (Chèn đề bài bài tập 1 tại đây)
Lời giải: (Chèn lời giải chi tiết bài tập 1 tại đây. Giải thích từng bước, sử dụng công thức và lý thuyết liên quan. Ví dụ: Để giải bài tập này, ta sử dụng công thức... Áp dụng công thức, ta có... Vậy kết quả là...)
Bài tập 2: (Ví dụ - cần thay thế bằng nội dung thực tế của trang 41)
Đề bài: (Chèn đề bài bài tập 2 tại đây)
Lời giải: (Chèn lời giải chi tiết bài tập 2 tại đây. Giải thích từng bước, sử dụng công thức và lý thuyết liên quan.)
Bài tập 3: (Ví dụ - cần thay thế bằng nội dung thực tế của trang 42)
Đề bài: (Chèn đề bài bài tập 3 tại đây)
Lời giải: (Chèn lời giải chi tiết bài tập 3 tại đây. Giải thích từng bước, sử dụng công thức và lý thuyết liên quan.)
Lưu ý quan trọng khi giải bài tập
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài tập trước khi bắt đầu giải.
- Xác định kiến thức cần sử dụng: Lựa chọn các định nghĩa, định lý, công thức phù hợp.
- Thực hiện các phép tính cẩn thận: Tránh sai sót trong quá trình tính toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả cuối cùng là chính xác.
Bảng tổng hợp công thức (Ví dụ - cần thay thế bằng công thức thực tế)
| Công thức | Mô tả |
|---|
| a2 + b2 = (a + b)2 - 2ab | Công thức tính bình phương của một tổng |
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Mục 1 trang 41, 42 Chuyên đề học tập Toán 11 - Kết nối tri thức. Tusach.vn luôn đồng hành cùng các em trên con đường học tập!
Tìm kiếm thêm:
- Giải Toán 11 Kết nối tri thức
- Chuyên đề Toán 11
- Bài tập Toán 11