Giải bài 1.15 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức
Bài 1.15 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất của dãy số để giải quyết các vấn đề thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.15 trang 20, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
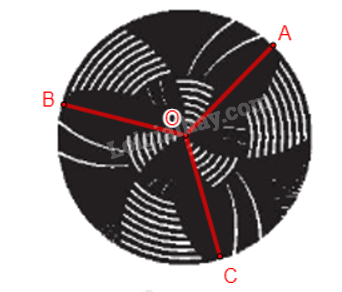
Bằng quan sát Hình 1.32, hãy chỉ ra một cách cắt hình đó thành ba phần giống nhau.
Giải bài 1.15 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết
Bài 1.15 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức thường xoay quanh các chủ đề về dãy số, cấp số cộng, cấp số nhân và ứng dụng của chúng trong các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
- Dãy số: Định nghĩa, các loại dãy số (dãy số hữu hạn, dãy số vô hạn, dãy số tăng, dãy số giảm).
- Cấp số cộng: Định nghĩa, công thức tính số hạng tổng quát, tổng n số hạng đầu.
- Cấp số nhân: Định nghĩa, công thức tính số hạng tổng quát, tổng n số hạng đầu.
- Ứng dụng: Giải các bài toán liên quan đến dãy số, cấp số cộng, cấp số nhân trong thực tế.
Phân tích bài toán và tìm hướng giải quyết
Trước khi bắt tay vào giải bài 1.15 trang 20, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, cần phân tích bài toán để tìm ra hướng giải quyết phù hợp. Thông thường, bài toán sẽ yêu cầu tính một số hạng của dãy số, tính tổng của một dãy số, hoặc tìm một số hạng thỏa mãn một điều kiện nào đó.
Lời giải chi tiết bài 1.15 trang 20
(Ở đây sẽ là lời giải chi tiết của bài 1.15 trang 20. Ví dụ minh họa, cần thay thế bằng lời giải thực tế)
Ví dụ: Giả sử bài toán yêu cầu tìm số hạng thứ 10 của một cấp số cộng có số hạng đầu là 2 và công sai là 3.
Lời giải:
Số hạng thứ n của một cấp số cộng được tính theo công thức: un = u1 + (n-1)d
Trong đó:
- un là số hạng thứ n
- u1 là số hạng đầu
- d là công sai
- n là số thứ tự của số hạng
Áp dụng công thức vào bài toán, ta có:
u10 = 2 + (10-1) * 3 = 2 + 9 * 3 = 2 + 27 = 29
Vậy số hạng thứ 10 của cấp số cộng là 29.
Lưu ý khi giải bài tập về dãy số và cấp số
- Luôn kiểm tra lại các công thức và tính toán.
- Chú ý đến điều kiện của bài toán để tránh sai sót.
- Rèn luyện kỹ năng giải bài tập thường xuyên để nắm vững kiến thức.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn cung cấp đầy đủ lời giải chi tiết, đáp án chính xác và phương pháp giải nhanh chóng cho tất cả các bài tập trong sách giáo khoa Toán 11 Kết nối tri thức. Hãy truy cập tusach.vn để học Toán 11 hiệu quả và đạt kết quả cao!
| Công thức | Mô tả |
|---|
| un = u1 + (n-1)d | Số hạng thứ n của cấp số cộng |
| Sn = n(u1 + un)/2 | Tổng n số hạng đầu của cấp số cộng |
| un = u1 * qn-1 | Số hạng thứ n của cấp số nhân |