Giải mục 1 trang 21, 22, 23 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 21, 22, 23 Chuyên đề học tập Toán 11 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 21, 22, 23 của Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của các em.
Các phép tịnh tiến, phép đối xứng trục, phép quay cùng có tính chất nào trong các tính chất sau?
Hoạt động
Các phép tịnh tiến, phép đối xứng trục, phép quay cùng có tính chất nào trong các tính chất sau?
a) Biến một vectơ thành vectơ bằng nó.
b) Biến một đường tròn thành một đường tròn cùng tâm.
c) Biến một đoạn thẳng thành đoạn thẳng bằng nó.
d) Biến một đường thẳng thành đường thẳng song song với nó.
Phương pháp giải:
Phép tịnh tiến, phép đối xứng trục, phép quaybảo toàn độ dài đoạn thẳng.
Lời giải chi tiết:
Các phép tịnh tiến, phép đối xứng trục, phép quay cùng có tính chất c) trong các tính chất đã cho:
c) Biến một đoạn thẳng thành đoạn thẳng bằng nó.
Luyện tập
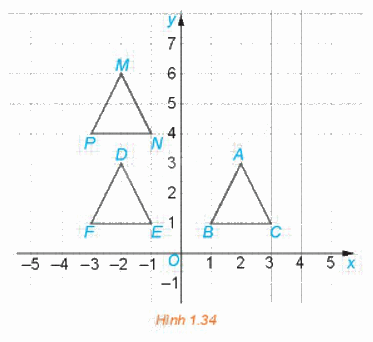
Trong mặt phẳng tọa độ Oxy ở Hình 1.34, gọi f là phép biến hình biến mỗi điểm có tọa độ \(\left( {x;{\rm{ }}y} \right)\)thành điểm có tọa độ \(\left( {-{\rm{ }}x;{\rm{ }}y{\rm{ }} + {\rm{ }}3} \right).\)Trong các khẳng định sau, những khẳng định nào đúng.
a) f biến \(\Delta \)ABC thành \(\Delta \)DEF.
b) f biến \(\Delta \)DEF thành \(\Delta \)MNP.
c) f biến \(\Delta \)ABC thành \(\Delta \)MNP.
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
Từ Hình 1.34, ta thấy: \(A\left( {2;{\rm{ }}3} \right),{\rm{ }}B\left( {1;{\rm{ }}1} \right),{\rm{ }}C\left( {3;{\rm{ }}1} \right),{\rm{ }}D\left( {-{\rm{ }}2;{\rm{ }}3} \right),{\rm{ }}E\left( {-{\rm{ }}1;{\rm{ }}1} \right),{\rm{ }}F\left( {-{\rm{ }}3;{\rm{ }}1} \right),{\rm{ }}M\left( {-{\rm{ }}2;{\rm{ }}6} \right),{\rm{ }}N\left( {-{\rm{ }}1;{\rm{ }}4} \right),{\rm{ }}P\left( {-{\rm{ }}3;{\rm{ }}4} \right).\)
+ Phép biến hình f biến điểm A(2; 3) thành điểm có tọa độ \(\left( {-{\rm{ }}2;{\rm{ }}3{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}2;{\rm{ }}6} \right)\) hay chính là điểm M.
Phép biến hình f biến điểm B(1; 1) thành điểm có tọa độ \(\left( {-{\rm{ }}1;{\rm{ }}1{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}1;{\rm{ }}4} \right)\) hay chính là điểm N.
Phép biến hình f biến điểm C(3; 1) thành điểm có tọa độ \(\left( {-{\rm{ }}3;{\rm{ }}1{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}3;{\rm{ }}4} \right)\) hay chính là điểm P.
Do đó, phép biến hình f biến tam giác ABC thành tam giác MNP nên khẳng định c) đúng và khẳng định a) sai.
+ Phép biến hình f biến điểm D(– 2; 3) thành điểm có tọa độ \(\left( {-{\rm{ }}\left( {-{\rm{ }}2} \right);{\rm{ }}3{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {2;{\rm{ }}6} \right).\)
Do đó, phép biến hình f không biến tam giác DEF thành tam giác MNP nên khẳng định b) sai.
Vậy trong các khẳng định đã cho, chỉ có khẳng định c) đúng.
Vận dụng
Trong tình huống mở đầu, bằng quan sát (H.1.33), hãy chỉ ra phép dời hình:
a) Biến Hình a) thành Hình b).
b) Biến Hình b) thành Hình c).
c) Biến Hình a) thành Hình c).
d) Biến Hình c) thành Hình a).
Phương pháp giải:
Quan sát hình 1.33, dựa vào các phép dời hình đã học để suy luận
Lời giải chi tiết:
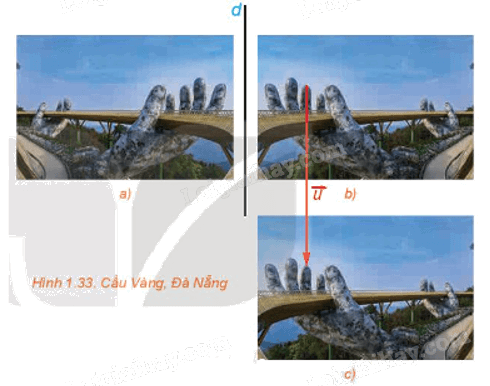
) Phép đối xứng trục d biến Hình a) thành Hình b).
b) Phép tịnh tiến theo vectơ \(\overrightarrow u \) biến Hình b) thành Hình c).
c) Thực hiện liên tiếp phép đối xứng trục d và phép tịnh tiến theo vectơ \(\overrightarrow u \) (thực hiện phép đối xứng trục d trước, phép tịnh tiến theo vectơ \(\overrightarrow u \) sau) ta được một phép dời hình biến Hình a) thành Hình c).
d) Thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow u \) và phép đối xứng trục d (thực hiện phép tịnh tiến theo vectơ \(\overrightarrow u \) trước và phép đối xứng trục d sau) ta được một phép dời hình biến Hình c) thành Hình a).
- Hoạt động
- Luyện tập
- Vận dụng
Các phép tịnh tiến, phép đối xứng trục, phép quay cùng có tính chất nào trong các tính chất sau?
a) Biến một vectơ thành vectơ bằng nó.
b) Biến một đường tròn thành một đường tròn cùng tâm.
c) Biến một đoạn thẳng thành đoạn thẳng bằng nó.
d) Biến một đường thẳng thành đường thẳng song song với nó.
Phương pháp giải:
Phép tịnh tiến, phép đối xứng trục, phép quaybảo toàn độ dài đoạn thẳng.
Lời giải chi tiết:
Các phép tịnh tiến, phép đối xứng trục, phép quay cùng có tính chất c) trong các tính chất đã cho:
c) Biến một đoạn thẳng thành đoạn thẳng bằng nó.
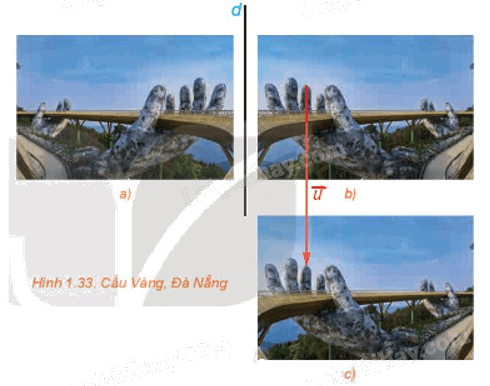
Trong mặt phẳng tọa độ Oxy ở Hình 1.34, gọi f là phép biến hình biến mỗi điểm có tọa độ \(\left( {x;{\rm{ }}y} \right)\)thành điểm có tọa độ \(\left( {-{\rm{ }}x;{\rm{ }}y{\rm{ }} + {\rm{ }}3} \right).\)Trong các khẳng định sau, những khẳng định nào đúng.
a) f biến \(\Delta \)ABC thành \(\Delta \)DEF.
b) f biến \(\Delta \)DEF thành \(\Delta \)MNP.
c) f biến \(\Delta \)ABC thành \(\Delta \)MNP.
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
Từ Hình 1.34, ta thấy: \(A\left( {2;{\rm{ }}3} \right),{\rm{ }}B\left( {1;{\rm{ }}1} \right),{\rm{ }}C\left( {3;{\rm{ }}1} \right),{\rm{ }}D\left( {-{\rm{ }}2;{\rm{ }}3} \right),{\rm{ }}E\left( {-{\rm{ }}1;{\rm{ }}1} \right),{\rm{ }}F\left( {-{\rm{ }}3;{\rm{ }}1} \right),{\rm{ }}M\left( {-{\rm{ }}2;{\rm{ }}6} \right),{\rm{ }}N\left( {-{\rm{ }}1;{\rm{ }}4} \right),{\rm{ }}P\left( {-{\rm{ }}3;{\rm{ }}4} \right).\)
+ Phép biến hình f biến điểm A(2; 3) thành điểm có tọa độ \(\left( {-{\rm{ }}2;{\rm{ }}3{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}2;{\rm{ }}6} \right)\) hay chính là điểm M.
Phép biến hình f biến điểm B(1; 1) thành điểm có tọa độ \(\left( {-{\rm{ }}1;{\rm{ }}1{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}1;{\rm{ }}4} \right)\) hay chính là điểm N.
Phép biến hình f biến điểm C(3; 1) thành điểm có tọa độ \(\left( {-{\rm{ }}3;{\rm{ }}1{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}3;{\rm{ }}4} \right)\) hay chính là điểm P.
Do đó, phép biến hình f biến tam giác ABC thành tam giác MNP nên khẳng định c) đúng và khẳng định a) sai.
+ Phép biến hình f biến điểm D(– 2; 3) thành điểm có tọa độ \(\left( {-{\rm{ }}\left( {-{\rm{ }}2} \right);{\rm{ }}3{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {2;{\rm{ }}6} \right).\)
Do đó, phép biến hình f không biến tam giác DEF thành tam giác MNP nên khẳng định b) sai.
Vậy trong các khẳng định đã cho, chỉ có khẳng định c) đúng.
Trong tình huống mở đầu, bằng quan sát (H.1.33), hãy chỉ ra phép dời hình:
a) Biến Hình a) thành Hình b).
b) Biến Hình b) thành Hình c).
c) Biến Hình a) thành Hình c).
d) Biến Hình c) thành Hình a).
Phương pháp giải:
Quan sát hình 1.33, dựa vào các phép dời hình đã học để suy luận
Lời giải chi tiết:
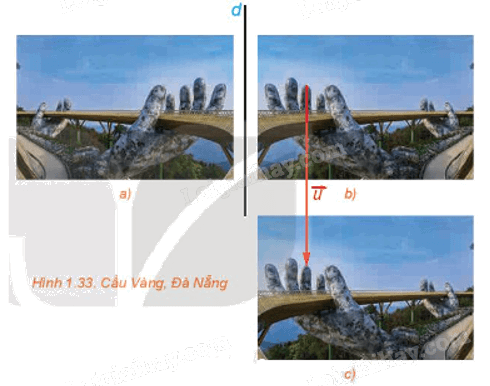
) Phép đối xứng trục d biến Hình a) thành Hình b).
b) Phép tịnh tiến theo vectơ \(\overrightarrow u \) biến Hình b) thành Hình c).
c) Thực hiện liên tiếp phép đối xứng trục d và phép tịnh tiến theo vectơ \(\overrightarrow u \) (thực hiện phép đối xứng trục d trước, phép tịnh tiến theo vectơ \(\overrightarrow u \) sau) ta được một phép dời hình biến Hình a) thành Hình c).
d) Thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow u \) và phép đối xứng trục d (thực hiện phép tịnh tiến theo vectơ \(\overrightarrow u \) trước và phép đối xứng trục d sau) ta được một phép dời hình biến Hình c) thành Hình a).
Giải mục 1 trang 21, 22, 23 Chuyên đề học tập Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt vào giải bài tập. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để đạt kết quả tốt. Tusach.vn sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục này, kèm theo các phân tích và giải thích rõ ràng.
Nội dung chính của Mục 1 (trang 21, 22, 23)
Để hiểu rõ hơn về Mục 1, chúng ta cần xác định các nội dung chính mà nó đề cập đến. Thông thường, đây có thể là:
- Lý thuyết trọng tâm: Các định nghĩa, định lý, tính chất quan trọng liên quan đến chủ đề.
- Ví dụ minh họa: Các bài toán mẫu giúp học sinh hiểu cách áp dụng lý thuyết vào thực tế.
- Bài tập luyện tập: Các bài toán với mức độ khó tăng dần, giúp học sinh rèn luyện kỹ năng giải toán.
Giải chi tiết bài tập trang 21
Bài 1: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích). Ví dụ: Bài 1 yêu cầu tính giới hạn của một hàm số. Chúng ta sẽ sử dụng các quy tắc tính giới hạn để tìm ra kết quả. Lưu ý kiểm tra điều kiện xác định của hàm số trước khi tính giới hạn.
Bài 2: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích).
Giải chi tiết bài tập trang 22
Bài 3: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích). Bài này có thể liên quan đến việc chứng minh một đẳng thức lượng giác. Cần sử dụng các công thức lượng giác cơ bản và biến đổi khéo léo để đạt được kết quả.
Bài 4: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích).
Giải chi tiết bài tập trang 23
Bài 5: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích). Bài 5 có thể là một bài toán ứng dụng thực tế. Cần đọc kỹ đề bài, xác định các yếu tố quan trọng và xây dựng mô hình toán học phù hợp.
Bài 6: (Nêu lại đề bài). Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích).
Mẹo học tập và ôn thi hiệu quả
- Nắm vững lý thuyết: Đọc kỹ sách giáo khoa, ghi chép các công thức và định lý quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập với các mức độ khó khác nhau để rèn luyện kỹ năng.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, hãy hỏi thầy cô, bạn bè hoặc tìm kiếm trên các trang web học tập uy tín như Tusach.vn.
- Ôn tập định kỳ: Thường xuyên ôn lại kiến thức đã học để củng cố và ghi nhớ lâu hơn.
Bảng tổng hợp các công thức quan trọng (Ví dụ)
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| tan x = sin x / cos x | Định nghĩa hàm tan |
Hy vọng với lời giải chi tiết và những chia sẻ trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và ôn thi môn Toán 11. Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức!